Wie wir in vorherigen Beiträgen gesehen haben, wird die Integralrechnung meist eingesetzt, um Flächen zwischen Graphen bzw. der x-Achse zu berechnen. Es gibt jedoch auch Integrale, die nicht zur Flächenberechnung benutzt werden können, denn sie sind in einer Richtung unendlich. Mit anderen Worten: Ihre Grenzen sind nicht definiert, sie haben einen unbeschränkten Integrationsbereich. Deshalb nennt man sie uneigentliches Integral. Diese treten bei e-Funktionen auf. Deshalb betrachte ich noch einmal die e-Funktionen und zeige Beispiele dazu. Schließlich zeige ich, wie man die Fläche unter einem uneigentlichen Integral und die Fläche unter einer zusammengesetzten Funktion berechnet.
Beispiele e-Funktionen
Im Folgenden zeige ich eine normale e-Funktion. Danach gespiegelt an der y-Achse. Dann in verschiedene Richtungen verschoben.
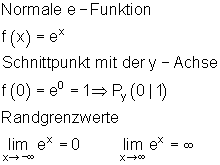
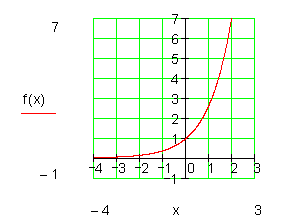

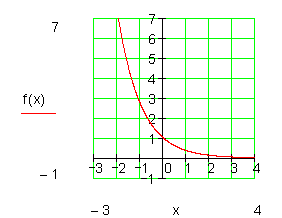

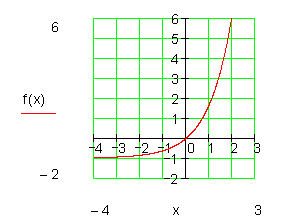

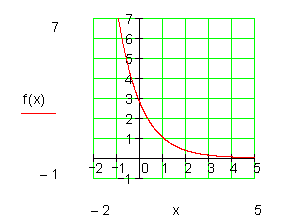
Fläche unter einem uneigentlichen Integral berechnen
Al nächstes versuchen ich, die Fläche unter solch einer Funktion zu berechnen:
Beispiel:
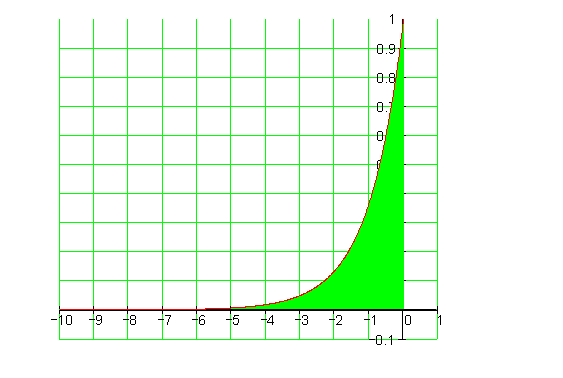
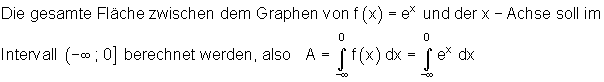
Bisher waren untere bzw. obere Grenze eines bestimmten Integrals Zahlen. Der Integrationsbereich war also begrenzt. Nun ist der Integrationsbereich nicht mehr begrenzt. Deshalb nennt man ein solches Integral Uneigentliches Integral mit unbeschränktem Integrationsbereich. Diese Integrale können in einer der drei Formen vorkommen.
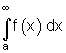
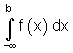
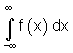
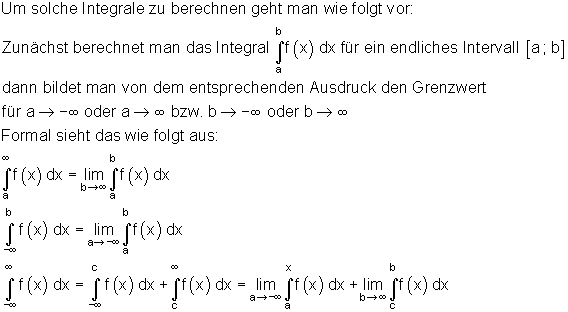
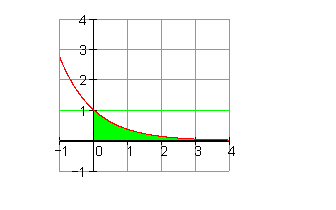
Für unsere Flächenberechnung sieht das wie folgt aus:
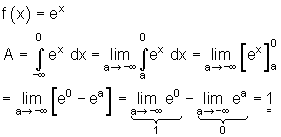
Weiteres Beispiel zu einem uneigentlichen Integral:
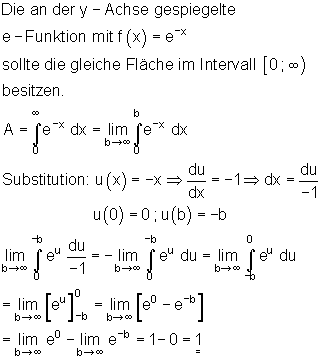
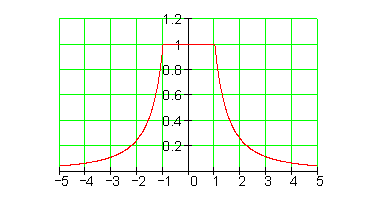
Fläche unter einer zusammengesetzten Funktion
Wir können zwei Funktionen zusammensetzten und die Fläche daruter berechnen. Denn diese Fläche ist jetzt nicht mehr unendlich.
Beispiel

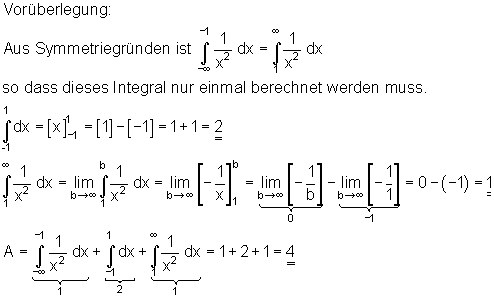
Hier findest du Aufgaben zur Differential- und Integralrechnung:
Aufgaben Integration der e-Funktion, Flächenberechnungen.
Und: Werbebanner und vermischte Aufgaben.
Hier Unterrichtsthemen und Aufgaben zur Abiturvorbereitung.
Hier eine Übersicht über alle Beiträge zur Fortgeschrittenen Differential- und Integralrechnung, darin auch Links zu weiteren Aufgaben.


