Hier findet ihr Aufgaben zur Integration der e-Funktion, uneigentliche Integrale und Flächenberechnungen.
1. Berechne folgende Integrale und skizziere die jeweilige Fläche.
a) \int \limits_{0}^{1} e^x \,dx
b) \int \limits_{-1}^{0} e^x \,dx
c) \int \limits_{-3}^{0} e^x \,dx
2. Berechne folgende Integrale und skizziere die jeweilige Fläche.
a) \int \limits_{0}^{1} (e^x - 1) \,dx
b) \int \limits_{0}^{3} (e^x - 1) \,dx
c) \int \limits_{- \infty }^{0} (e^x - 1) \,dx
3. Berechne folgende Integrale und skizziere die jeweilige Fläche.
a) \int \limits_{0}^{1} e^{-x} \,dx
b) \int \limits_{-1}^{2} e^{-x} \,dx
c) \int \limits_{0}^{\infty} e^{-x} \,dx
4. Berechne folgende Integrale und skizziere die jeweilige Fläche.
a) \int \limits_{0}^{3} e^{-(x-3)} \,dx
b) \int \limits_{1}^{3} e^{-(x-2)} \,dx
c) \int \limits_{3}^{\infty} e^{-(x-3)} \,dx
5. Berechne folgende Integrale.
a) \int \limits_{0}^{3} (e^x - x + 1) \,dx
b) \int \limits_{0}^{4} 3 \cdot e^{x+2} \,dx
c) \int \limits_{0}^{5} (e^x + e^{-x}) \,dx
6. Für welches k hat das Integral den angegebenen Wert?
a) \int \limits_{0}^{2} k \cdot e^x \,dx = \frac{1}{2} e
b) \int \limits_{0}^{4} (e^x - k \cdot x) \,dx = 4
c) \int \limits_{0}^{k} e^x \,dx = 2 \cdot e
7. Berechne folgende Integrale.
a) \int \limits_{0}^{ln(2)} (e^{2x} - 2e^x) \,dx
b) \int \limits_{0}^{ln(k)} (e^{2x} - k \cdot e^x) \,dx
c) \int \limits_{0}^{4} (\frac{1}{4} e^x - 2e^{\frac{1}{2}x}) \,dx
8. Berechne folgende Integrale und skizziere die jeweilige Fläche.
a) f(x) = e^x - 1 für 0 ≤ x ≤ 2
g(x) = f(2) \cdot e^{-(x-2)} für 2 ≤ x < ∞
A = \int \limits_{0}^{2} f(x) \,dx +\int \limits_{2}^{\infty} g(x) \,dx
b) f(x) = e^x - 1 für 0 ≤ x ≤ 3
g(x) = f(3) \cdot e^{-(x-3)} für 3 ≤ x < ∞
A = \int \limits_{0}^{3} f(x) \,dx +\int \limits_{3}^{\infty} g(x) \,dx
9. Berechne folgende Integrale.
a)
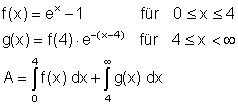
b)
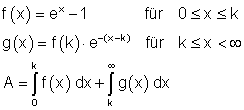
Hier findest du die ausführlichen Lösungen.
Hier die dazugehörige Theorie: Integration der e-Funktion.
Außerdem hier: Differentations- und Integrationsregeln.
Hier findest du eine Übersicht über weitere Beiträge zur Fortgeschrittenen Differential- und Integralrechnung, darin auch Links zu weiteren Aufgaben.

