In diesem Beitrag beschäftige ich mich mit der Integration der e-Funktion. Dazu zeige ich den Zusammen zwischen Stammfunktion und Integrandenfunktion. Dann stelle ich das allgemeine und das bestimmte Integral mit Substitution vor. Am Schluss stelle ich Aufgaben zur Verfügung.
- Zusammenhang zwischen Stammfunktion und Integrandenfunktion
- Beispiel
- Allgemeines Integral mit Substitution
- Bestimmtes Integral mit Substitution
- Trainingsaufgaben zum Integrieren von e-Funktionen
Zusammenhang Stammfunktion und Integrandenfunktion
In der Integralrechnung haben wir folgende Zusammenhänge kennengelernt:
Wenn man eine beliebige integrierbare Funktion f(x) integriert, erhält man eine Stammfunktion: F(x) = \int^f(x) dx
Die Funktion f(x) wird deshalb Integrandenfunktion genannt.
Es gilt: \color{red}{F(x) = \int^f(x)dx \Leftrightarrow F'(x) = f(x)}
Mit anderen Worten: leitet man die Stammfunktion ab, so erhält man wieder die Integrandenfunktion. Deshalb ermöglicht dieser Zusammenhang es uns, durch Ableiten das Ergebnis der Integration zu überprüfen.
Beispiel für die Integration der e-Funktion:
![]()
Wir wissen inzwischen, dass sich die e-Funktion bei der Ableitung selber reproduziert. Wenn man dies auf die e-Funktion anwendet, gilt:
Wenn F(x) = \int f(x) dx = e^x + C die Menge aller Stammfunktionen von f(x), dann ist
F'(x) = f(x) = [e^x + C]' = e^x .
| Integration der e-Funktion: 💡 \color{red}{\large{\int e^x dx = e^x + C}} 💡 |
Bei der Ableitung der e-Funktion sollte man in den Fällen, in denen der Exponent der e-Funktion nicht nur aus der Variablen x bestand, die Kettenregel verwenden. Bei der Integration sollte man die Integrandenfunktion so substituieren, dass man mit der Regel (1) integrieren kann.
Allgemeines Integral mit Substitution
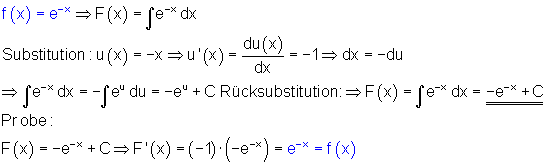
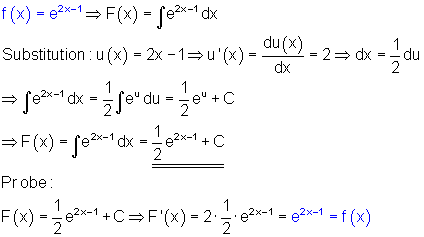
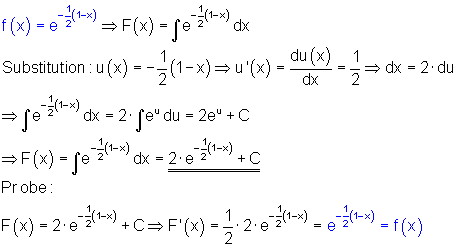
Bestimmtes Integral mit Substitution
Wenn man Flächen zwischen dem Graphen und der x-Achse berechnet, muss man stets ein bestimmtes Integral lösen. Hier führt die Methode der Substitution ebenfalls zum Ziel. Für die Lösung des Integrals durch Substitution gibt es dabei zwei verschiedene Varianten.

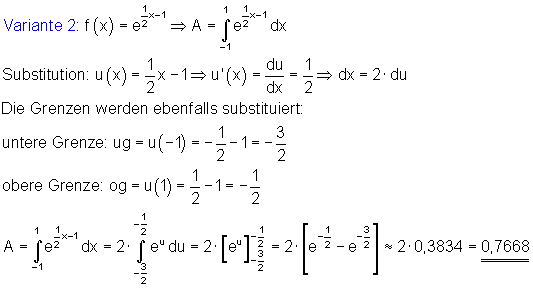
In der Variante 2 wurden untere und obere Grenze des bestimmten Integrals ebenfalls substituiert. In den meisten Fällen wird dadurch der Rechenaufwand etwas verringert.
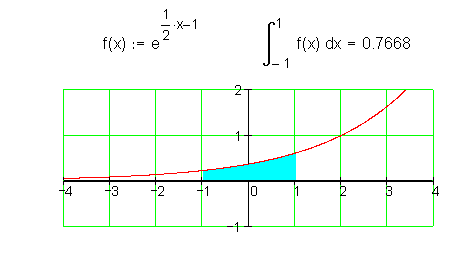
Aufgaben: Integriere folgende e-Funktionen!
Kontrolliere das Ergebnis von Aufgabe 1 bis 4 ist mit einer Probe!
1.![]()
2.![]()
3.![]()
4.![]()
.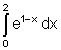
6.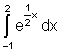
7.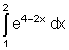
8.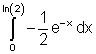
9.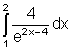
10.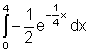
Hier findest du die Lösungen.
Weitere Aufgaben hierzu: Aufgaben Integration der e-Funktion, Flächenberechnungen.
Hier findest du eine Übersicht über weitere Beiträge zur Fortgeschrittenen Differential- und Integralrechnung, darin auch Links zu weiteren Aufgaben.


