Ableitungen e-Funktion mit Produktregel Kettenregel

e-Funktion, Funktionen, Mathematik


Wenn ihr eine einfache Version der Ableitung der e-Funktion sucht, seid ihr hier richtig! (Auch auf die Gefahr hin, dass einigen Mathematikern die Haare zu Berge stehen!) Anschließend zeige ich, wie man die Kettenregel und die Produktregel bei e-Funktionen einsetzt. Dann stelle ich noch Mehrfachableitungen vor. Schließlich verlinke ich Aufgaben.

  1. Anschauliche Ableitung der e-Funktion
  2. Grundregeln zum Ableiten von e-Funktionen:
  3. Kettenregel
  4. Produktregel
  5. Beispiele
  6. Mehrfachableitungen
  7. Link zu Trainingsaufgaben

Anschauliche Ableitung der e-Funktion (heuristisch)

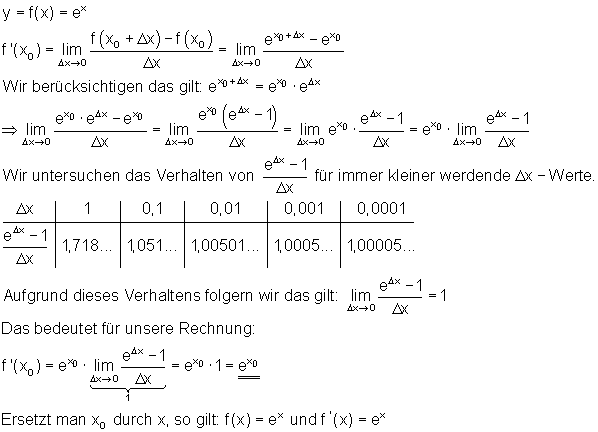
Ableitung-e-Funktion

Funktion und Ableitungsfunktion gleich

Die Exponentialfunktion f(x) = ex hat die Ableitungsfunktion f'(x) = ex.
Bei der Exponentialfunktion zur Basis e sind Funktion und Ableitungsfunktion also gleich.
Mit anderen Worten: Die e-Funktion reproduziert sich bei ihrer Ableitung.

Grundregeln zum Ableiten von e-Funktionen

Bei Spiegelungen, Streckungen und Verschiebungen der e-Funktion enthält der Exponent neben der Variable x noch weitere Werte oder Variablen. Verknüpfungen mit anderen Funktionen lassen neue Funktionen entstehen, in denen die e-Funktion als Faktor enthalten ist. In solchen Fällen sind für die Ableitungen weitere Regeln erforderlich.

Die Verschiebung der e-Funktion um 3 EH in positive x-Richtung und eine Streckung in x-Richtung mit dem Faktor 2 bewirkt eine Verkettung zweier Funktionen.
Deshalb stelle ich hier zwei Regeln vor:

Kettenregel bei der e-Funktion

e-Funktion-Kettenregel

Produktregel bei der e-Funktion

Betrachten wir die Verknüpfung einer e-Funktion mit einer linearen Funktion:

e-Funktion-Produktregel

Beispiele zur Produktregel bei der e-Funktion

(1)f_1392

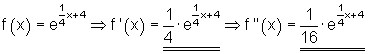
(2)f_1393

(3)
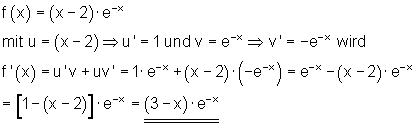
f_1394

(4)
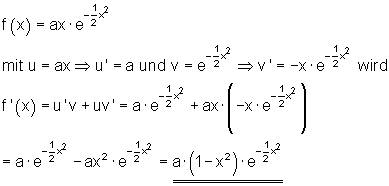
f_1395

Mehrfachableitungen

Im Zusammenhang mit Kurvendiskussionen braucht man oft drei Ableitungen der zu untersuchenden Funktion.

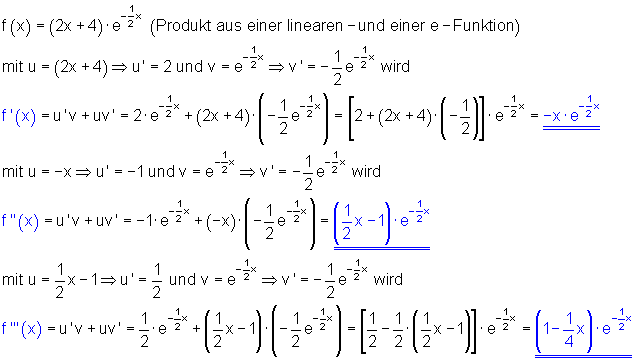
f_1396

Bei jeder Ableitung bleibt der e-Funktionsfaktor unverändert. Klammert man ihn aus, so ist die weitere Ableitung einfacher zu bewerkstelligen. Die Nullstelle der Ableitungsfunktion können wir oft einfach ablesen.

Übrigens hat Gottfried Wilhelm Leibniz  die Produktregel entwickelt, siehe Wikipedia.

Hier findest du Trainingsaufgaben zu Ableitungen der e-Funktion mit Produkt- und Kettenregel.

Und hier eine Übersicht über alle Beiträge zur Fortgeschrittenen Differential- und Integralrechnung, darin auch Links zu weiteren Aufgaben.

Außerdem hier die Playlist aller Videos zur Differentialrechnung.

Ähnliche Beiträge