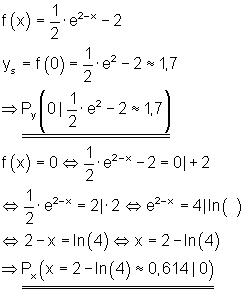Nachdem wir uns mit Exponentialfunktionen und der e-Funktion beschäftigt haben, zeige ich hier, wie man die Achsenschnittpunkte dieser Funktionen berechnen kann. Zuerst gebe ich hierzu ein paar Beispiele. Danach wiederhole ich kurz die Potenz- und Logarithmengesetze. Denn diese braucht man für die Trainingsaufgaben zur Anwendung der Potenz- und Logarithmengesetze. Anschließend zeige ich verschiedene Lösungsmethoden für Exponentialgleichungen: Lösung mittels Exponentenvergleich, Logarithmieren und Substitution. Ich zeige ausführliche Beispiele zu Exponentialgleichungen und stelle Trainingsaufgaben dazu vor. Zuletzt zeige ich, wie man Achsenschnittpunkte berechnet.
-
- Beispiele Achsenschnittpunkte e-Funktion berechnen
- Potenz- und Logarithmengesetze
- Aufgaben Potenz- und Logarithmengesetze
- Lösungsmethoden für Exponentialgleichungen
- Beispiele zu Achsenschnittpunkte Exponentialgleichungen
- Aufgaben Exponentialgleichungen
- Achsenschnittpunkte von Exponentialgleichungen
- Link zu Aufgaben
Einführungsbeispiel Achsenschnittpunkte e-Funktion berechnen
Beispiel 1 Achsenschnittpunkte Exponentialgleichungen:
Zu bestimmen sind die Achsenschnittpunkte von

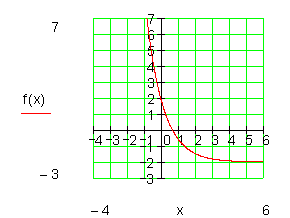
Schnittpunkte mit der x-Achse bestimmt man über die Nullstellen von f (x). Die Funktion f (x) hat keine Nullstelle, da es sich bei ihr um eine in x- Richtung verschobene und in x-Richtung gestreckte e-Funktion handelt. Sie ist außerdem noch an der y-Achse und an der x-Achse gespiegelt.

Beispiel 2 Achsenschnittpunkte Exponentialgleichungen:
Zu bestimmen sind die Achsenschnittpunkte von
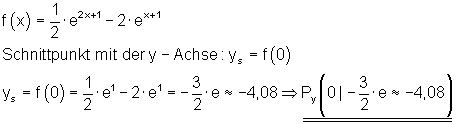
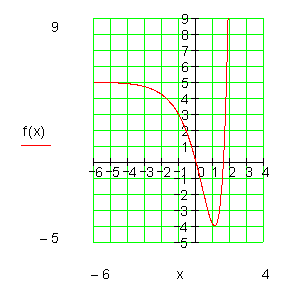
Um mögliche Schnittpunkte mit des x-Achse zu bestimmen, ist der Aufwand etwas größer. Dazu sind die Nullstellen von f (x) zu bestimmen.

Um die Schnittpunkte mit der x-Achse, also die Nullstellen einer Exponentialfunktion zu bestimmen, ist es in vielen Fällen erforderlich, eine Exponentialgleichung zu lösen.
Zusätzlich zu den bekannten Operationen, die zur Lösung von Gleichungen verwendet werden, ist es bei der Lösung von Exponentialgleichungen nötig, die Potenz- und die Logarithmengesetze zu kennen.
Potenz- und Logarithmengesetze
Da wir im folgenden die Potenz- und Logarithmengesetze brauchen werden, habe ich hier noch einmal die wichtigsten zusammengefasst:

Im Zusammenhang mit e-Funktionen haben Potenzen mit der Basis e und natürliche Logarithmen eine besondere Bedeutung.
Aufgaben: Anwendung der Potenz- und Logarithmengesetze
Forme folgende Potenz- und Logarithmenterme unter Verwendung der Potenz- und Logarithmengesetze um.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
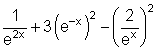
6.
![]()
7.
![]()
8.
![]()
9.![]()
10.
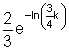
Hier findest du die Lösungen.
Lösungsmethoden für Exponentialgleichungen
Lösung mittels Exponentenvergleich

Eine Lösung mittels Exponentenvergleich ist nur dann möglich, wenn es gelingt, die Terme auf beiden Seiten der Gleichung so umzuformen, dass sich Potenzen mit gleichen Basen ergeben. Das ist leider jedoch nicht immer möglich, wie folgendes Beispiel zeigen soll.
Lösung mittels Logarithmieren
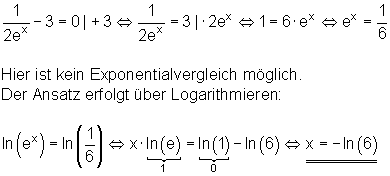
In vielen Fällen führt der Ansatz über das Logarithmieren zum Erfolg. Jedoch Exponentialgleichungen, in denen Summen oder Differenzen vorkommen, können nicht logarithmiert werden. Man kann versuchen, sie mittels Substitution (Einsetzung einer Ersatzvariablen) zu lösen.
Lösung mittels Substitution

Ausführliche Beispiele zu Achsenschnittpunkte Exponentialgleichungen

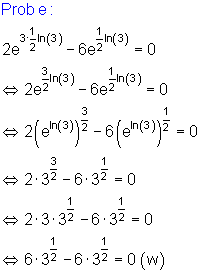

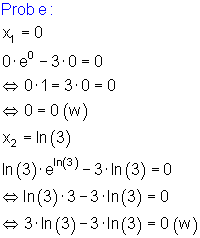

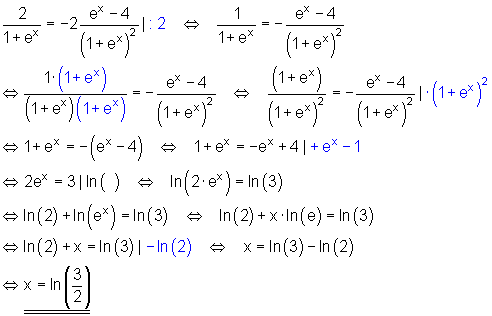

Aufgaben: Exponentialgleichungen:
Löse die folgenden Exponentialgleichungen mit den dir bekannten Methoden!
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
Die Lösungen hierzu findest du hier.
Achsenschnittpunkte von Exponentialgleichungen