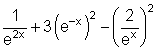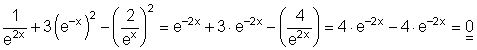Hier findest du die Lösungen der Aufgaben zu Achsenschnittpunkten von Exponentialgleichungen.
Teil I
1.
Vereinfache mit den dir bekannten Potenz- und Logarithmengesetzen folgenden Term:
![]()
Ausführliche Lösung :
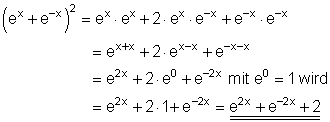
2.
Vereinfache mit den dir bekannten Potenz- und Logarithmengesetzen folgenden Term:
![]()
Ausführliche Lösung ;
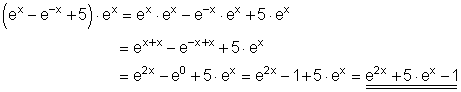
3.
Vereinfache mit den dir bekannten Potenz- und Logarithmengesetzen folgenden Term:
4.
Vereinfache mit den dir bekannten Potenz- und Logarithmengesetzen folgenden Term.:
Ausführliche Lösung:
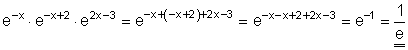
5.
Vereinfache mit den dir bekannten Potenz- und Logarithmengesetzen folgenden Term:
6.
Vereinfache mit den dir bekannten Potenz- und Logarithmengesetzen folgenden Term:
![]()
Ausführliche Lösung:
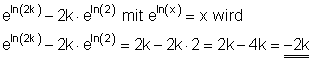
7.
Vereinfache mit den dir bekannten Potenz- und Logarithmengesetzen folgenden Term:
![]()
Ausführliche Lösung:
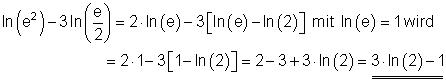
8.
Vereinfache mit den dir bekannten Potenz- und Logarithmengesetzen folgenden Term:
![]()
Ausführliche Lösung:
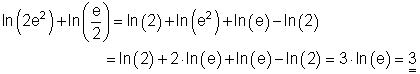
9.
Vereinfache mit den dir bekannten Potenz- und Logarithmengesetzen folgenden Term:
![]()
Ausführliche Lösung:
![]()
10.
Vereinfache mit den dir bekannten Potenz- und Logarithmengesetzen folgenden Term:
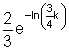
Ausführliche Lösung:
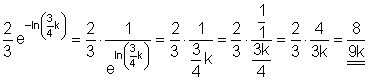
Teil 2
1.
Löse die Exponentialgleichung:
![]()
Ausführliche Lösung;
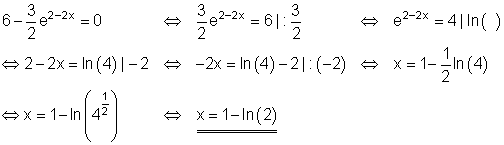
Lösung durch logarithmieren.
2.
Löse die Exponentialgleichung:
![]()
Ausführliche Lösung:
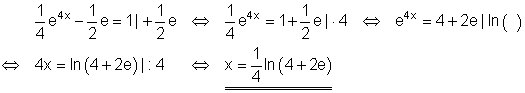
Lösung durch logarithmieren.
3.
Löse die Exponentialgleichung:
![]()
Ausführliche Lösung:
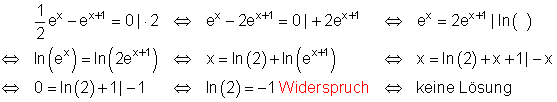
Lösung durch logarithmieren. Wenn bei der Lösung einer Gleichung ein Widerspruch auftritt, dann hat sie keine Lösung.
4.
Löse die Exponentialgleichung:
![]()
Ausführliche Lösung:
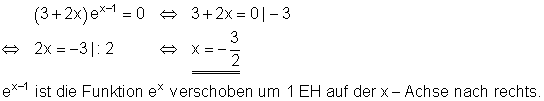
Lösung nach dem Satz vom Nullprodukt. Ein Produkt ist genau dann Null, wenn mindestens ein Faktor Null ist. Da die e-Funktion nicht Null wird, kann nur der Faktor ( 3 + 2x ) Null werden.
5.
Löse die Exponentialgleichung:
![]()
Ausführliche Lösung:

Lösung nach dem Satz vom Nullprodukt. Die e-Funktion wird nicht Null.
6.
Löse die Exponentialgleichung:
![]()
Ausführliche Lösung:
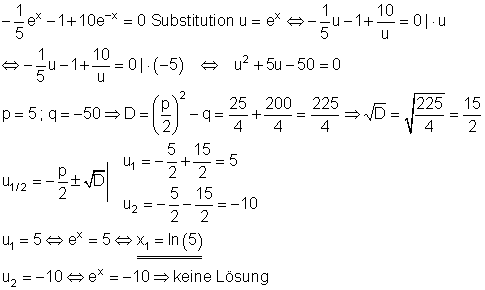
Lösung durch Substitution. Beim Zurücksubstituieren ist darauf zu achten, dass der Logarithmus nur für positive Zahlen größer Null definiert ist.
7.
Löse die Exponentialgleichung:
![]()
Ausführliche Lösung:
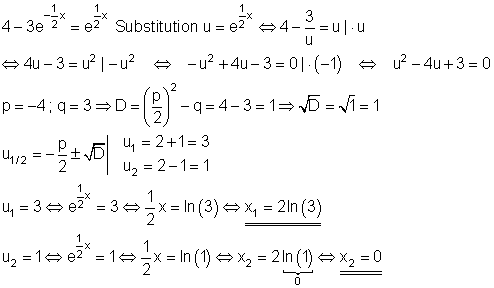
Lösung durch Substitution.
8.
Löse die Exponentialgleichung:
![]()
Ausführliche Lösung:
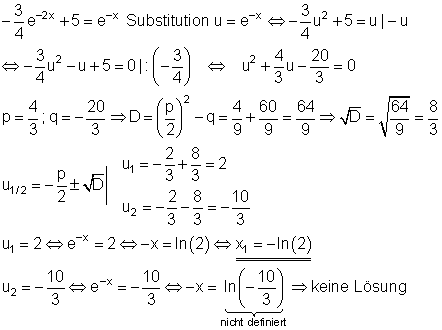
Lösung durch Substitution.
9.
Löse die Exponentialgleichung:
![]()
Ausführliche Lösung:
![]()
10.
Löse die Exponentialgleichung:
![]()
Ausführliche Lösung:
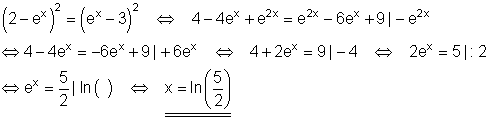
Lösung durch logarithmieren.
Hier findest du die Theorie und Aufgaben hierzu.
Und hier eine Übersicht über alle Beiträge zum Thema Differential- und Integralrechnung, darin auch Links zur Theorie und zu weiteren Aufgaben.