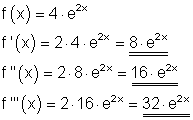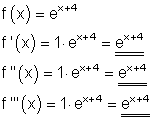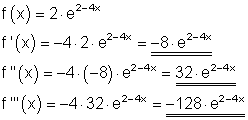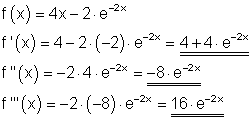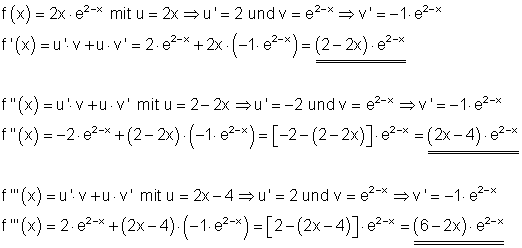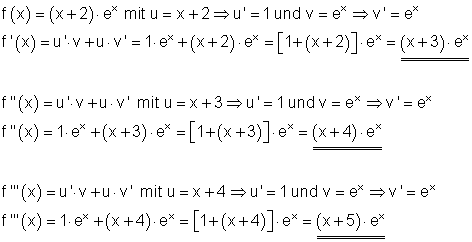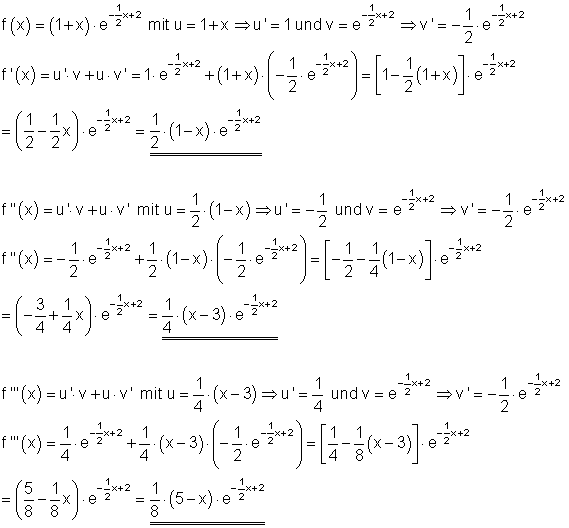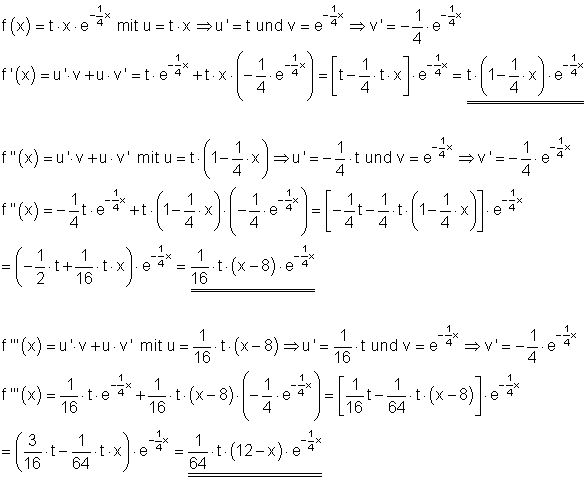Hier findest du die Lösungen zu den Aufgaben zu Ableitungen der e-Funktion mit Produktregel und Kettenregel mit komplettem Lösungsweg.
Ich wünsche allen viel Erfolg!
1. Ausführliche Lösung:
2. Ausführliche Lösung:
3. Ausführliche Lösung:
4. Ausführliche Lösung:
5. Ausführliche Lösung:
f(x) = x \cdot e^{-2x} mit u = x \\ \Rightarrow u' = 1
\quad und \quad v = e^{-2x} \\ \Rightarrow v' = -e^{-2x}
f'(x) = u' \cdot v + u \cdot v' \\ = 1 \cdot e^{-2x} + x \cdot (-2 \cdot e^{-2x} ) \\ = 1 \cdot e^{-2x} - 2x \cdot e^{-2x} \\ =
\underline{\underline{ (1 - 2x) \cdot e^{-2x} }}
f''(x) = u' \cdot v + u \cdot v' mit u = 1 - 2x \\ \Rightarrow u'
= -2 und v = e^{-2x} \\ \Rightarrow v' = -2 \cdot e^{-2x}
f''(x) = -2 \cdot e^{-2x} + (1 - 2x) \cdot ( -2 \cdot e^{-2x} ) \\
= [-2 - 2 \cdot (1 - 2x)] \cdot e^{-2x} = \underline{\underline{(4x - 4) \cdot e^{-2x} }}
f'''(x) = u' \cdot v + u \cdot v' mit u = 4x - 4 \\ \Rightarrow u' = 4 und v = e^{-2x} \\ \Rightarrow v' = -2 \cdot e^{-2x}
f'''(x) = 4 \cdot e^{-2x} + (4x - 4) \cdot (-2 \cdot e^{-2x}) \\ = [4 - 2 \cdot (4x - 4)] \cdot e^{-2x} \\ = \underline{\underline{(12 - 8x) \cdot e^{-2x} }}
6. Ausführliche Lösung:
7. Ausführliche Lösung:
8. Ausführliche Lösung:
f(x) = (1 - x) \cdot e^{\frac{1}{2}x} mit \quad
u = 1 - x \\ \Rightarrow u' = -1 und v' = e^{\frac{1}{2}x} \\ \Rightarrow v' = \frac{1}{2} \cdot e^{\frac{1}{2}x}
f'(x) = u' \cdot v + u \cdot v' \\ = - 1 \cdot e^{\frac{1}{2}x} + (1 - x) \cdot \frac{1}{2} e^{\frac{1}{2}x}
\\ = [ -1 + \frac{1}{2} (1 - x)] \cdot e^{\frac{1}{2}x} \\ = \underline{\underline{(-\frac{1}{2} - \frac{1}{2}x) \cdot e^{\frac{1}{2}x} }}
f''(x) = u' \cdot v + u \cdot v' mit u = -\frac{1}{2} - \frac{1}{2}x \\ \Rightarrow u' = -\frac{1}{2} und v = e^{\frac{1}{2}x}
\\ \Rightarrow v' = \frac{1}{2} \cdot e^{\frac{1}{2}x}
f''(x) = -\frac{1}{2} \cdot e^{\frac{1}{2}x} + (-\frac{1}{2} - \frac{1}{2}x) \cdot \frac{1}{2} \cdot e^{\frac{1}{2}x} \\ = [-\frac{1}{2} + \frac{1}{2} (-\frac{1}{2} - \frac{1}{2}x) ] \cdot e^{\frac{1}{2}x}
= \underline{\underline{ (-\frac{3}{4} - \frac{1}{4}x) \cdot e^{\frac{1}{2}x} }}
f'''(x) = u' \cdot v + u \cdot v' mit u = -\frac{3}{4} - \frac{1}{4}x \\ \Rightarrow u' = -\frac{1}{4} und v = e^{\frac{1}{2}x} \\ \Rightarrow v' = \frac{1}{2} \cdot e^{\frac{1}{2}x}
f'''(x) = - \frac{1}{4} \cdot e^{\frac{1}{2}x} + (-\frac{3}{4} - \frac{1}{4}x) \cdot \frac{1}{2} e^{\frac{1}{2}x}
\\ = [-\frac{1}{4} + \frac{1}{2} (-\frac{3}{4} - \frac{1}{4}x)] \cdot e^{\frac{1}{2}x} \\ = \underline{\underline{(-\frac{5}{8} - \frac{1}{8}x) \cdot e^{\frac{1}{2}x} }}
9. Ausführliche Lösung:
10. Ausführliche Lösung:
Hier findest du die Aufgaben hierzu.
Hier die Theorie: Ableitungen der e-Funktion mit Produkt- und Kettenregel.
Und hier eine Übersicht über alle Beiträge zur Fortgeschrittenen Differential- und Integralrechnung.
Dazu kannst du auch den Wikipediaartikel über die Produktregel lesen.
Und hier die Playlist aller Videos zur Differentialrechnung.
