In diesem Beitrag findet ihr zuerst die ausführlichen Lösunge einer Aufgabe zur Integralrechnung mit einem Werbebanner. Danach weitere Lösungen zu den Anwendungsaufgaben aus der Differential- und Integralrechnung, Anforderungen: Ableitung, Extremwerte, Fläche zwischen Graphen, e-Funktion, Produktregel, Kettenregel, Nullprodukt, waagerechte Tangente.
1. Lösung Aufgabe Integralrechnung Werbebanner
Ausführliche Lösungen:
a)
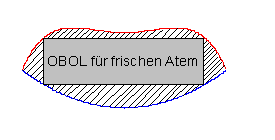
Der untere Teil des Mundes wird durch eine quadratische Funktion beschrieben. Der obere Teil des Mundes durch eine ganzrationale Funktion 4. Grades.

b)
Da die Graphen der Funktionen f(x) und g(x) symmetrisch zur y-Achse verlaufen, ist auch das einbeschriebene Rechteck symmetrisch zur y-Achse. Die y-Achse teilt die Rechteckseite a in zwei gleichlange Teile. Um die Seite b des Rechtecks in Abhängigkeit von a zu bestimmen, benötigt man die Koordinaten der oberen und unteren rechten Ecke des Rechtecks.
![]()
Die absolute Differenz der y-Koordinaten ergibt die Seite b. Dazu berechnen wir zuerst die jeweiligen y-Koordinaten der Eckpunkte.
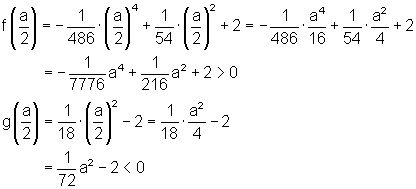
Für die Länge der Seite b gilt also:
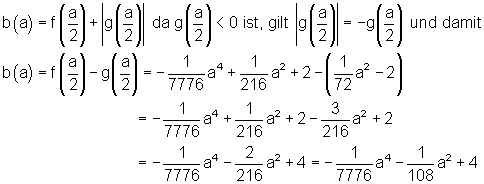
Da die Seite b von a abhängt, sagt man auch b ist eine Funktion von a also b(a). Die Fläche des Rechtecks A ist das Produkt seiner Seiten.
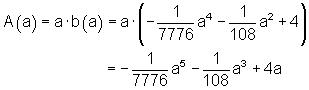
Die Extremwertbestimmung von A(a) liefert den Wert von a, für dass die Rechteckfläche am größten wird.
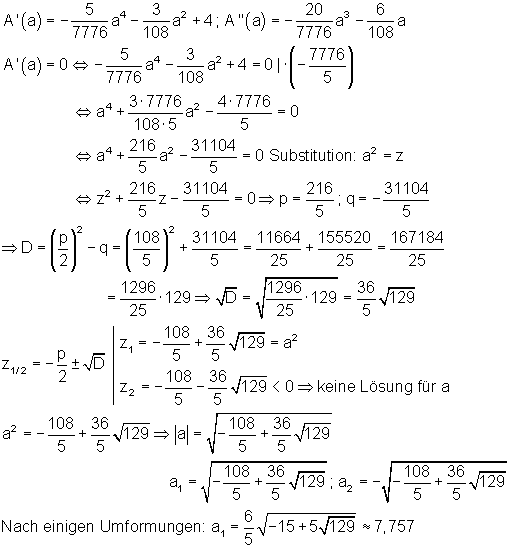
Da aus z2 keine Wurzel gezogen werden kann und der Wert für a positiv sein soll, müsste a1 eine Extremstelle von A(a) sein. Das ist mit der 2. Ableitung von A(a) zu überprüfen.
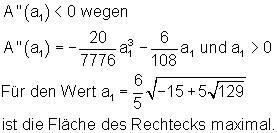
Da der Graph, der den oberen Teil des Mundes bildet, an der Stelle x = 0 ein Minimum aufweist ( PMin ( 0 | 2 )), ist zu überprüfen, ob die obere Seite des Rechtecks unterhalb davon liegt.

Die Berechnung erfolgte mit dem Taschenrechner. Das Ergebnis bestätigt, dass die obere Seite des Rechtecks unterhalb des Minimums von f(x) liegt.
Nun kann die Fläche des Rechtecks mit dem Taschenrechner berechnet werden:
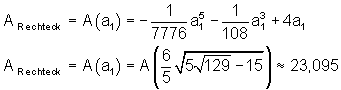
Das Rechteck maximaler Größe hat eine Fläche von etwa 23,095 m2.
c)
Die gesamte Fläche des Mundes ist die Fläche zwischen den Funktionsgraphen von f(x) und g(x). Diese ist über die Integration zu finden. Dazu müssen aber zuerst die Integrationsgrenzen bestimmt werden.
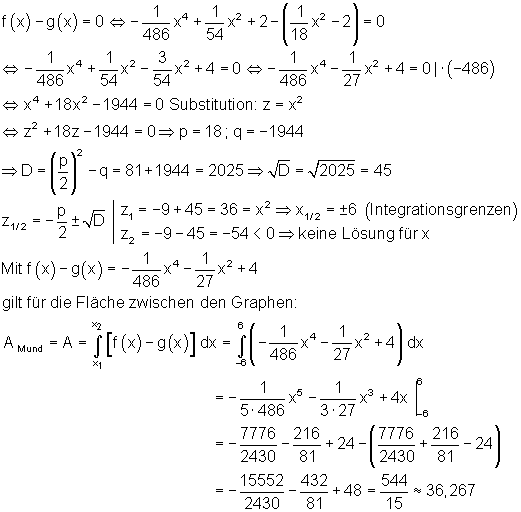
Für den Mund wird an der Hauswand eine Fläche von insgesamt 36,267 m2 benötigt. d)
Die schraffierte Fläche ist die Differenz aus der gesamten Fläche und der des Rechtecks.

Bemerkung zu Rundungsfehlern
Um Rundungsfehler möglichst zu vermeiden, sollte man bei Berechnungen mit dem Taschenrechner Zwischenwerte speichern. In vielen Fällen reicht aber für die Berechnung eine Genauigkeit von 3 Stellen hinter dem Komma. Im folgenden soll die Rechnung mit einer Genauigkeit von 3 Stellen hinter dem Komma durchgeführt werden.
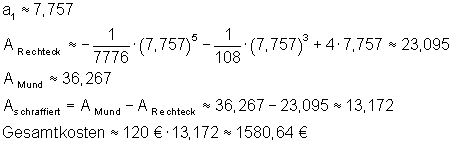
2. Bestimme die Fläche
Ausführliche Lösung:
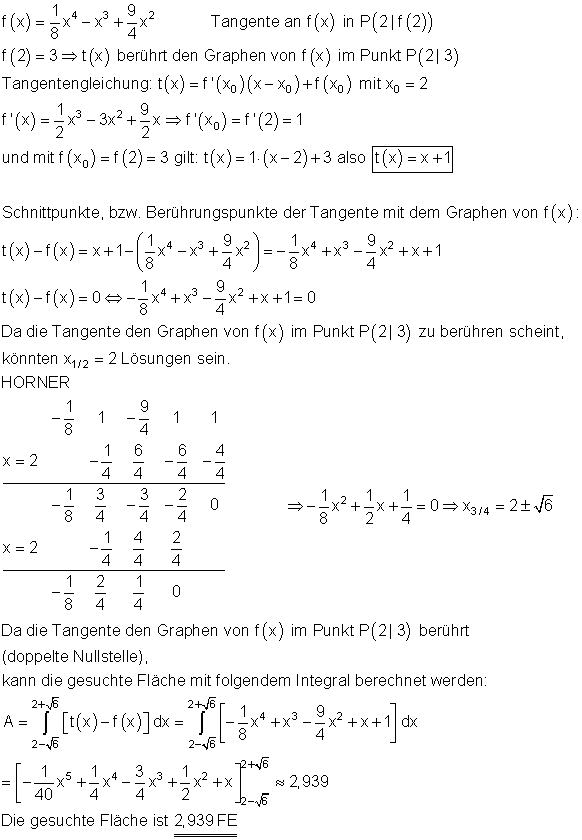
3. Nullstellen, Tangente
Ausführliche Lösung:
a)

b)

![]()
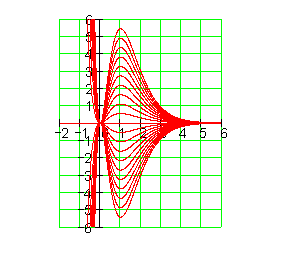
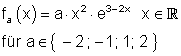

Hier findest du die Aufgaben hierzu.
Und hier die Theorie: Differentations- und Integrationsregeln.
Hier eine Übersicht über alle Beiträge zur Fortgeschrittenen Differential- und Integralrechnung, darin auch Links zu weiteren Aufgaben.

