Hier findet ihr vermische Aufgaben zur Differential- und Integralrechnung. Anforderungen sind dabei: Potenz- und Logarithmenterme, Exponentialgleichungen, Wertetabelle, Ganzrationale Funktionen, Tiefpunkt, Achsenschnittpunkte, Ableitung, Tangentengleichung, Gauß-Algorithmus, Extremwerte, Nullstellen, biquadratische Gleichung, bestimmtes Integral.
1. Forme um
Forme folgende Potenz- und Logarithmenterme unter Verwendung der Potenz- und Logarithmengesetze um.
a)
![]()
b)
![]()
2. Löse die Exponentialgleichungen
mit den dir bekannten Methoden.
a)
![]()
b)
![]()
3. Aufgaben Differentialrechnung
a)
![]()
b)
![]()
4. Aufgaben Integralrechnung
Kontrolliere die Ergebnisse indem du ableitest
a)
![]()
b)
![]()
5. Aufgaben Differentialrechnung
Setze dabei die bekannten Regeln ein
a)
![]()
b)
![]()
6. Aufgaben Integralrechnung
a)
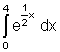
b)
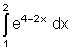
7. Aufgaben Differentialrechnung: Minimum
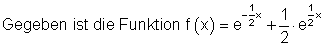
a) Stelle für [ -4 ; 5 ] eine Wertetabelle auf und skizziere den Graphen. Kennzeichne danach die Fläche unter dem Graphen zwischen der y-Achse, der Parallelen zur y-Achse durch den Tiefpunkt und der x-Achse.
b) Berechne dann das relative Minimum T ( xe | f(xe) ).
c) Berechne schließlich die unter a) gekennzeichnete Fläche.
8. Aufgaben Differentialrechnung Tangente
Der Graph einer ganzrationalen Funktion 3. Grades schneidet die x-Achse in P ( -4 | 0 ) und hat in T ( 2 | 0 ) einen Tiefpunkt. Außerdem schneidet die Tangente an P die y-Achse in Py ( 0 | 48 ). Berechne zuerst die Funktionsgleichung von f(x). Danach die Gleichung der Tangente t(x). Skizziere schlißelich die Graphen.
Anforderungen (Link zur entsprechenden Theorie):
Ganzrationale Funktionen, Tiefpunkt, Achsenschnittpunkte, Ableitung, Tangentengleichung, Gauß-Algorithmus.
9. Aufgaben Differentialrechnung: Extremwerte
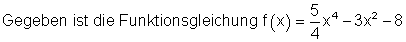
Bestimme zuerst die Extremwerte. Berechne danach die Fläche zwischen dem Graphen und der x-Achse. Dabei bilden die Nullstellen die Integrationsgrenzen. Zeichne dann den Graphen. Kennzeichne schließlich die berechnete Fläche.
Anforderungen dabei sind: Extremwerte, Nullstellen, biquadratische Gleichung, bestimmtes Integral.
Hier findest du die Lösungen hierzu.
Und hier die Theorie hierzu: Differentations- und Integrationsregeln.
Und hier eine Übersicht über alle Beiträge zur Fortgeschrittenen Differential- und Integralrechnung, darin auch Links zu weiteren Aufgaben.
Dazu kannst auch den Wikipedia-Artikel zur Differentialrechnung lesen.


