Hier erkläre ich zuerst, wie man die Achsenschnittpunkte quadratischer Funktionen berechnet. Dazu stelle ich Trainingsaufgaben zur Verfügung. Außerdem einen interaktiven Parabelanalysator, einen Nullstellenfinder und einen Parabelplotter. Danach lasse ich ein paar Bemerkungen zum Betrag und zur Definitions- und Wertemenge fallen. Anschließend zeige ich anhand eines anschaulichen Beispiels die Symmetrie quadratischer Funktionen. Den Scheitelpunkt über die Nullstellen berechnen ist sehr einfach, die Lösung einer quadratischen Gleichung mittels quadratischer Ergänzung dagegen nicht so. Danach erkläre ich den Zusammenhang zwischen Diskriminante und Lösungsmenge und zwischen Lösungsmenge und Funktionsgraph. Der Satz von Vieta ist ebenfalls nützlich für die Ergebniskontrolle. Zuletzt zeige ich, wie man quadratische Funktionen mit vorgegebenen Nullstellen konstruieren kann.
Achsenschnittpunkte mit der y-Achse
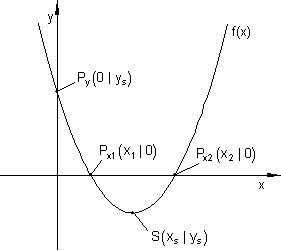
Bei der Betrachtung des Graphen in dieser Abbildung fallen einige Punkte besonders auf.

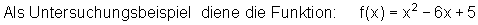
Der Graph schneidet die y-Achse im Punkt Py.
Für jeden Punkt, der auf der y-Achse liegt, ist die x-Koordinate Null.
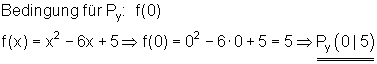
In diesem Fall hätten wir die y-Koordinate auch direkt aus der Funktionsgleichung ablesen können. Das ist aber nur möglich, wenn man die Klammer auflöst. Dazu folgendes Beispiel:
Beispiel für einen Achsenschnittpunkte mit der y-Achse
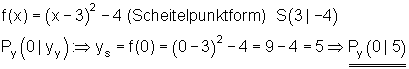
Wenn wir die Klammer auflösen: (x - 3)^2 - 4 = x^2 - 6x + 9 - 4 = x^2 - 6x +5
Achsenschnittpunkte mit der x-Achse
Der Graph schneidet die x-Achse in den Punkten Px1 und Px2.
Für jeden Punkt, der auf der x-Achse liegt, ist die y-Koordinate Null.
Beispiel für einen Achsenschnittpunkte mit der x-Achse

Hier findest du Trainingsaufgaben hierzu.
Parabelanalysator Interaktiv: Wenn du die Koeffizienten der Funktionsgleichung eingibst, analysiert das Javascript danach die Parabel und zeichnet sie.
Bemerkungen zum Betrag
Jemand gewinnt 120 €, anders ausgedrückt er gewinnt einen Geldbetrag von 120 €.
Jemand bekommt einen Strafzettel über 120 €, mit anderen Worten er hat einen Geldbetrag von 120 € zu zahlen.
In beiden Fällen handelt es sich um 120 €.
Finanztechnisch bedeutet der Gewinn ein Plus und die Strafe ein Minus.
Der Betrag einer Zahl ist jedoch mathematisch immer positiv.
Dazu kannst du dir das 📽️Video Betrag in der Mathematik ansehen.
Soll der Betrag einer Variablen bestimmt werden, dann brauchen wir eine Rechenvorschrift.

Beispiel:

Zu weiteren Betrachtungen zeichnen wir den Graphen unserer Beispielfunktion.
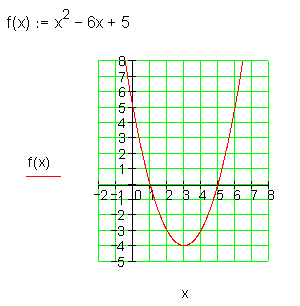
Es handelt sich um eine nach oben geöffnete Normalparabel, deren Scheitel in den Punkt S ( 3 | – 4 ) verschoben wurde.
Der Schnittpunkt mit der y-Achse ist Py ( 0 | 5 )
Die Schnittpunkte mit der x-Achse sind Px1 ( 1 | 0 ) und Px2 ( 5 | 0 )
Die Schnittpunkte mit der x-Achse nennen wir Nullstellen der Funktion f(x), da dort gilt: f (1) = 0 und f (5) = 0.
Definitions- und Wertemenge
Oft will man den Verlauf eines Graphen nur in einem bestimmten Bereich betrachten.
Das führt zu den Begriffen Definitionsmenge und Wertemenge.
Unsere Beispielfunktion soll nur im Bereich der x-Werte von x = -1 bis x = +6 auf die dort auftretenden Funktionswerte untersucht werden.

Die Angabe einer Wertemenge bezieht sich immer auf eine Definitionsmenge.
Zu weiteren Betrachtungen zeichnen wir den Graphen unserer Beispielfunktion.
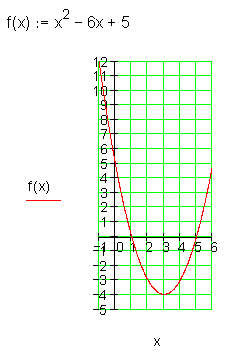
Die nebenstehende Abbildung zeigt genau den Ausschnitt des Funktionsgraphen, der durch die Definitionsmenge vorgegeben wurde.
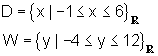
Symmetrie quadratischer Funktionen
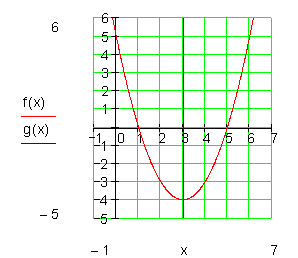
Die abgebildete Parabel ist symmetrisch zu der Achse, die parallel zur y-Achse durch den Scheitelpunkt verläuft.
Das gilt für alle Parabeln.
Die Gleichung der Symmetrieachse durch den Scheitel S( xs | ys ) lautet x = xs hier x = 3.
Auch die Nullstellen sind symmetrisch zur Symmetrieachse. Das bedeutet, bei bekannten Nullstellen kann der x-Wert des Scheitels berechnet werden.
Scheitelpunkt über die Nullstellen berechnen
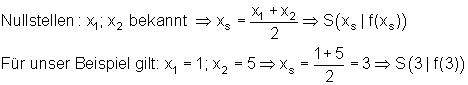
Sind die Nullstellen einer quadratischen Funktion bekannt, dann ist das arithmetische Mittel dieser die x-Koordinate des Scheitelpunktes.
Lösung einer quadratischen Gleichung mittels quadratischer Ergänzung
Eine Möglichkeit der Nullstellenbestimmung einer quadratischen Funktion geht über die Lösung einer quadratischen Gleichung mittels quadratischer Ergänzung. Man kann dafür auch eine Lösungsformel entwickeln.
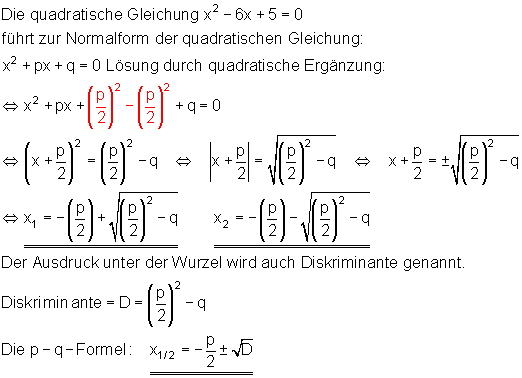
Die Nullstellen unserer Beispielfunktion sollen nun über die p-q-Formel berechnet werden:
f(x) = x^2 - 6x + 5 = 0
\Rightarrow p = -6 ; q = 5
Zuerst berechnen wir die Diskriminante D:
D = (\frac{p}{2})^2 - q = (-3)^2 - 5 = 9 - 5 = 4
x_{1,2} = -\frac{p}{2} \pm \sqrt D = 3 \pm \sqrt 4 \Rightarrow \underline{\underline{x_1 = 3 + 2 = 5 \lor x_2 = 3 - 2 = 1}}
Die Schnittpunkte mit der x-Achse sind also P1 (0 | 1) und P2 (0 | 5)
Der Scheitelpunkt S liegt genau in der Mitte, hat folglich die x-Koordinate (5 + 1) : 2 = 3
Um die y-Koordinate zu berechnen, setzen wir diesen Wert in die Funktion ein:
f(x) = x^2 - 6x + 5 = 0
\Rightarrow f(4) = 3^2 - 6 \cdot 3 + 5 = 9 - 18 + 5 = -4
Der Scheitelpunkt S hat also die Koordinaten (3 | -4}
Dazu kannst du dir dieses 📽️ Video Scheitelpunkt quadratischer Funktionen bestimmen ansehen.
Diskriminante und Lösungsmenge
Quadratische Gleichungen sind nicht immer lösbar.
Beispiel:
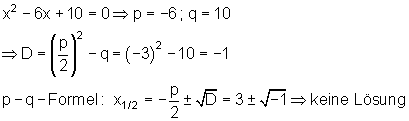
Hat die Diskriminante einen negativen Wert, so ist die quadratische Gleichung nicht lösbar, denn Wurzeln sind nur für positive Zahlen definiert.
Quadratische Gleichungen können auch nur eine Lösung besitzen.
Beispiel:
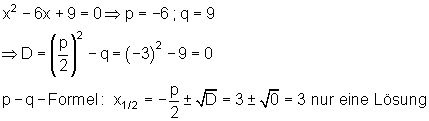
Zusammenfassung

Lösungsmenge und Funktionsgraph quadratischer Funktionen
Welche Bedeutung hat die Lösungsmenge einer quadratischen Gleichung auf den Verlauf des Funktionsgraphen einer quadratischen Funktion?
In den Beispielen hatten wir drei quadratische Gleichungen, mit jeweils zwei, keiner oder nur einer Lösung.
Wir zeichnen die Funktionsgraphen hierzu.
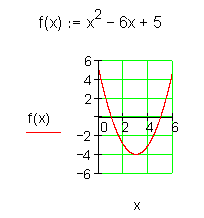
Zwei Nullstellen
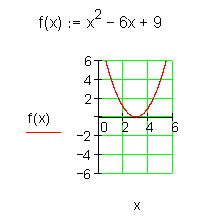
Eine Nullstelle
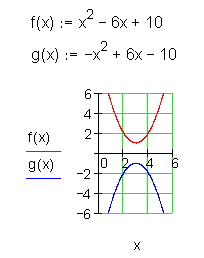
Keine Nullstelle
Bei zwei Nullstellen schneidet der Funktionsgraph die x-Achse zweimal.
Bei einer Nullstelle berührt der Funktionsgraph die x-Achse dagegen mit dem Scheitel.
Liegt keine Nullstelle vor, dann liegt der Scheitel einer nach oben geöffneten Parabel oberhalb der x-Achse, der Scheitel einer nach unten geöffneten Parabel unterhalb der x-Achse.
Nullstellenfinder Interaktiv: Wenn du eine Gleichung oder ein Polynom bis 9. Grades eingibst, errechnet das JavaScript anschließend die Nullstellen.
Parabelplotter Interaktiv: Gib die Koefizienten ein, danach zeichnet das JavaScript die Parabel.
Der Satz von Vieta
Satz:

Beweis:
Der Beweis folgt durch direkte Rechnung:
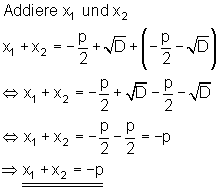
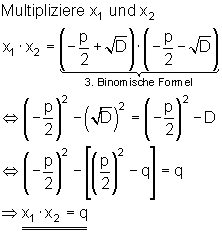
Der Satz von Vieta ist ganz nützlich für die Ergebniskontrolle der Lösung einer quadratischen Gleichung.
Beispiel:
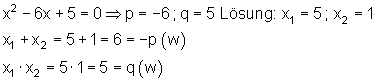
Quadratische Funktionen mit vorgegebenen Nullstellen konstruieren

Eine quadratische Gleichung von der die Nullstellen bekannt sind, kann auch als Produkt von Linearfaktoren geschrieben werden.
Satz vom Nullprodukt:
Ein Produkt ist genau dann Null, wenn mindestens ein Faktor Null ist.
Für die quadratische Gleichung unserer Beispielfunktion bedeutet das:
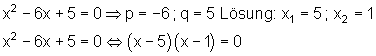
Nun können wir selber quadratische Funktionen mit vorgegebenen Nullstellen konstruieren:
Es soll eine quadratische Funktion mit den Nullstellen x1 = -2 und x2 = 3 entwickelt werden, die nach unten geöffnet ist und den Formfaktor ¾ besitzt.
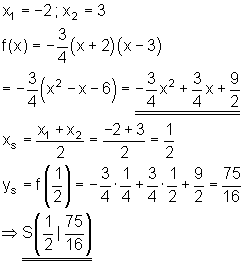
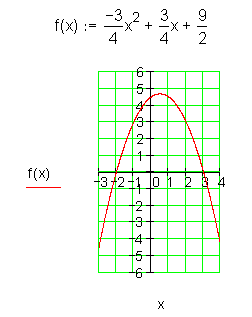
Parabelanalysator Interaktiv: Wenn du die Koeffizienten der Funktionsgleichung eingibst, analysiert das Javascript danach die Parabel und zeichnet sie.
Im nächsten Beitrag geht es um Schnittpunkte von Parabel und Gerade.
Hier eine Übersicht über weitere Beiträge zu Quadratischen Funktionen, darin auch Links zu weiteren Aufgabe.


