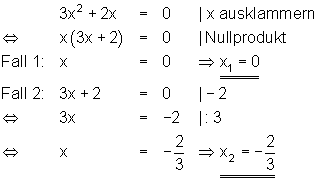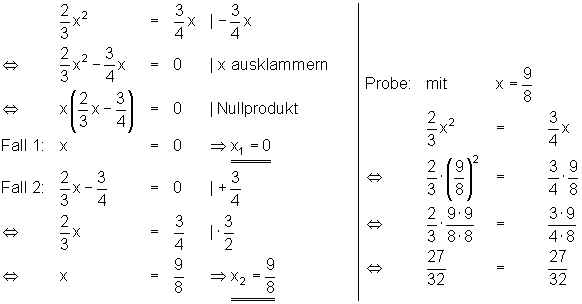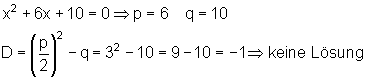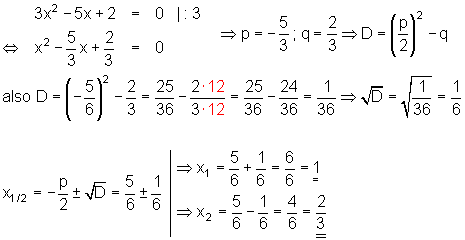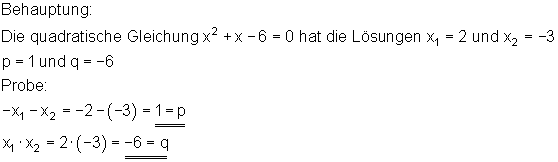Hier findest du eine leicht verständliche Einführung in Quadratische Gleichungen und die p-q-Formel.
Bis jetzt haben wir uns mit Gleichungen beschäftigt, bei denen die Variable x nur in der 1. Potenz steht, also lineare Gleichungen. In diesem Beitrag gebe ich eine Einführung in das Lösen quadratischer Gleichungen, also in denen x potenziert wird, siehe Potenzen, Wurzeln und ihre Rechengesetze. Dazu werde ich zuerst anhand eines anschaulichen Beispiels zeigen, wie man eine reinquadratische Gleichung durch Äquivalenzumformung löst. Dann werde ich kurz erklären, dass sich der Betrag einer reellen Zahl ergibt sich, wenn wir das Vorzeichen auf + umwandeln. Anschließend werde ich zwei Lösungsvarianten für reinquadratische Gleichungen und das Lösungsverfahren mit Hilfe der quadratischen Ergänzung vorstellen. Danach werde ich die allgemeine Form der quadratischen Gleichung erklären. Anhand einiger Beispiele werde ich dann die die p-q-Formel vorstellen. Schließlich werde ich zeigen, wie man die Lösungskontrolle mit dem Wurzelsatz von Vieta durchführt und wie man quadratische Gleichungen mittels Linearfaktoren konstruieren kann.
- Rein quadratische Gleichung
- Der Betrag in der Mathematik
- Rein quadratische Gleichungen mittels Wurzelziehen lösen
- Quadratische Gleichungen mittels Ausklammern lösen
- Allgemeine Form der quadratischen Gleichung
- Quadratische Gleichungen mittels quadratischer Ergänzung lösen
- p-q-Formel
- Nullstellen quadratischer Gleichungen
- Lösungskontrolle mit dem Satz von Vieta
- Quadratische Gleichungen mittels Linearfaktoren konstruieren
- Zusammenfassung
- Weiterführende Links und Links zu Aufgaben
1. Rein quadratische Gleichung
Eine quadratische Gleichung enthält eine Variable im Quadrat z. B. x^2 .
Eine rein quadratische Gleichung enthält die Variable nur im Quadrat, also kein 2x.

Das kannst du dir auch in diesem 📽️ shorts Rein quadratische Gleichungen ansehen.
2. Der Betrag in der Mathematik
Jemand gewinnt 120 €, wir sagen auch er gewinnt einen Geldbetrag von 120 €.
Jemand bekommt einen Strafzettel über 120 €, wir sagen auch er hat einen Geldbetrag von 120 € zu zahlen.
Finanztechnisch bedeutet der Gewinn ein Plus und die Strafe ein Minus.
![]()
In beiden Fällen handelt es sich um 120 €.
Der Betrag einer reellen Zahl ergibt sich, wenn wir das Vorzeichen auf + umwandeln.
Das kannst du dir auch in diesem 📽️ shorts Betrag in der Mathematik ansehen.
Beispiele zum Betrag:
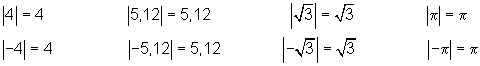
Nicht ganz so einfach ist es, wenn wir den Betrag einer Variablen x bestimmen wollen.
| x | = x gilt leider nicht für alle reellen Zahlen.
Beispiel zum Betrag mit Variablen:

Der Betrag einer reellen Zahl ist immer positiv.
Der Betrag gibt die Größe einer Zahl an, ohne dabei auf das Vorzeichen zu achten.
3. Rein quadratische Gleichungen mittels Wurzelziehen lösen
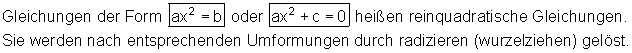
Nur rein quadratische Gleichungen kann man mittels Wurzelziehen lösen.
Beispiel
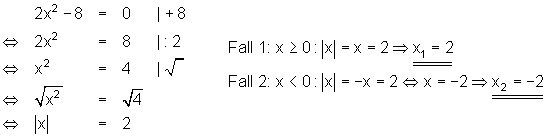
Beispiel:
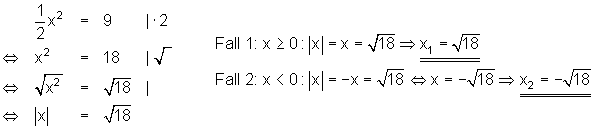
Dazu kannst du dir das 📽️ Video Rein Quadratische Gleichung lösen Wurzelziehen ansehen.
4. Quadratische Gleichungen mittels Ausklammern lösen

Satz vom Nullprodukt:
Ein Produkt ist genau dann Null, wenn mindestens ein Faktor Null ist.
Quadratische Gleichung durch Ausklammern lösen:

Beispiel:
Beispiel:
Dazu kannst du dir das 📽️ Video Quadratische Gleichung lösen Ausklammern ansehen.
5. Allgemeine Form der quadratischen Gleichung
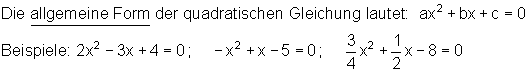
Für die nächsten Schritte empfiehlt es sich, wenn wir diese Darstellung zu vereinfachen.
Dazu dividieren wir beide Seiten der Gleichung durch a und erhalten die Normalform.
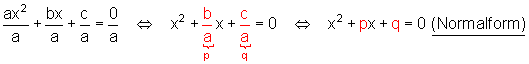
Die beiden Variablen p und q brauchen wir auch demnächst.
6. Lösungsverfahren mit Hilfe der quadratischen Ergänzung
Beispiel:
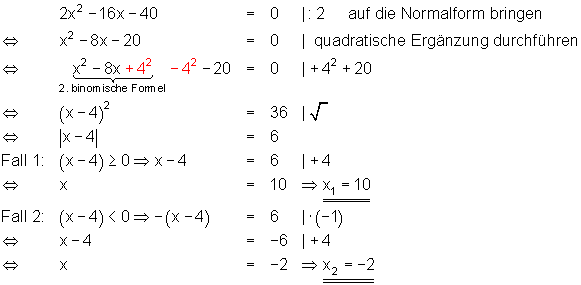
Jede quadratische Gleichung lässt sich mit der Methode der quadratischen Ergänzung lösen.
Bemerkung zur Ergänzung der Quadrates:
Man halbiert, quadriert, addiert und subtrahiert wieder den Koeffizient von x, also in diesem Fall die 8.
Unter Verwendung der 1. oder 2. binomischen Formel bildet man dann das Quadrat.
Dazu kannst du dir das 📽️ Video Quadratische Ergänzung ansehen.
7. Beispiele für die p-q-Formel
Die p-q-Formel sieht auf den ersten Blick kompliziert aus, aber wenn man die quadratischen Ergänzung verstanden hat, ist sie noch einfacher. Außerdem kann sie eine Menge Rechenarbeit ersparen.
Hier die Herleitung:
Wenn man die Normalform der quadratischen Gleichung mit Hilfe der quadratischen Ergänzung löst, kommt man zu diesem Ergebnis:
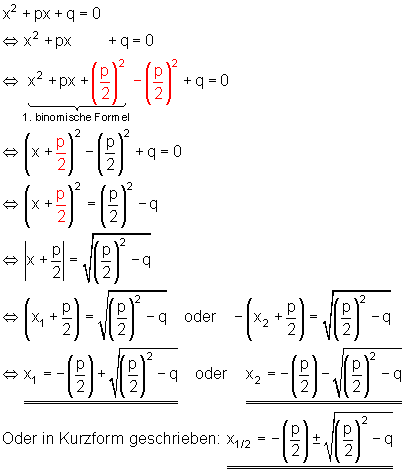
Mithilfe dieser Formel in der letzten Zeile brauchen wir also nur noch x1 und x2 auszurechnen.
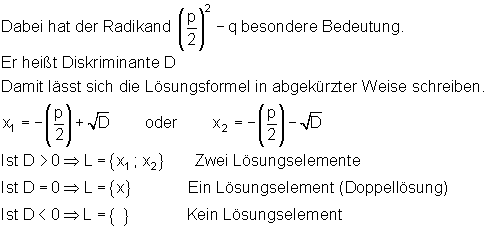
Wenn man zuerst die Diskriminante bestimmt, kennt man die Anzahl der Lösungen. Wenn es keine Lösung gibt, spart man sich die Rechenarbeit.
Dazu kannst du dir das 📽️ Video P-Q-Formel einfach erklärt ansehen.
Beispiel:
Beispiel:
Ein weiteres Beispiel kannst du dir auch in diesem 📽️ Video P-Q-Aufgaben ansehen.
8. Nullstellen von quadratischen Funktionen
Um die Nullstellen einer quadratischen Funktion zu bestimmen, ist stets eine quadratische Gleichung zu lösen.
Hat diese zwei Lösungselemente, so schneidet der Graph der quadratischen Funktion die x – Achse an zwei Stellen.
Hat sie nur eine Lösung, so berührt der Graph die x – Achse an einer Stelle (mit ihrem Scheitelpunkt).
Ist kein Lösungselement vorhanden, so verläuft der Graph oberhalb oder unterhalb der x – Achse, es gibt keinen Schnittpunkt.
Parabelplotter Nach Eingabe der Koeffizienten der Funktionsgleichung, kann die Parabel gezeichnet werden.
9. Lösungskontrolle mit dem Wurzelsatz von Vieta:
Wie bei jeder Gleichung kann die Lösung dadurch kontrolliert werden, dass man die Lösungselemente in die Ursprungsgleichung einsetzt, also die Probe macht.
Mit dem Wurzelsatz von Vieta geht es jedoch auch einfacher:
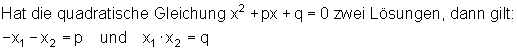
Durch einfaches einsetzen in die Normalform kann man das beweisen:
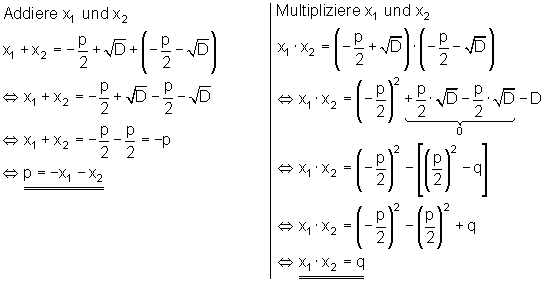
Beispiel:
Es lassen sich umgekehrt mit dem Satz von Vieta auch quadratische Gleichungen konstruieren, die ganz bestimmte Lösungen haben.
Beispiel:
10. Quadratische Gleichungen mittels Linearfaktoren konstruieren
Beispiel:
11. Zusammenfassung quadratische Gleichungen

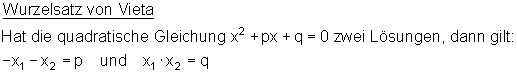

Dazu kannst due dieses Thema hier vertiefen: Achsenschnittpunkte, p-q-Formel und Linearfaktoren.