In diesem Beitrag erkläre ich als erstes, was lineare Gleichungen sind. Dann definiere ich Lösungsmenge, Definitionsmenge und Grundmenge. Anschließend zeige ich anhand vieler Beispiele, wie man mit der Äquivalenzumformung arbeitet. Dann stelle ich Gleichungen ohne und mit unendlich vielen Lösungen vor. Schließlich gebe ich Tipps für Anfänger und Fortgeschrittene.
- Was ist eine Gleichung?
- Definitionen: Lösungsmenge, Grundmenge, Definitionsmenge
- Äquivalenzumformung
- Beispiele
- Keine oder unendlich viele Lösungen
- Tipps für Anfänger und Fortgeschrittene
In dem Beitrag Terme und binomische Formeln haben wir gesehen, was Terme sind. Es sind Ausdrücke, in denen Variable und/oder Zahlen mit Rechenzeichen verbunden werden. Z. B.: x + 5 = 7.
Was ist eine Gleichung?
Wenn wir zwei Terme durch ein Gleichheitszeichen miteinander verbinden, dann entsteht eine Gleichung.
Enthält die Gleichung die Variable x nur in der 1. Potenz, dann spricht man von einer linearen Gleichung. Z. B.: x + 5 = 7.
Wenn höchstens x2 in einer Gleichung auftaucht, spricht man von quadratischen Gleichungen. Es gibt außerdem noch viele andere Gleichungen.
Dazu kannst du dir dieses 📽️ shorts Lineare Gleichungen, was ist das? ansehen.
Gleichungen lösen bedeutet: Welche Werte kann man für x einsetzen? All diese Werte nennt man die
Definition Lösungsmenge (L)
Gleichungen lösen bedeutet also „Bestimmen der Lösungsmengen“. Alle Werte schreibt man in eine geschweifte Klammer {}. Z. B. in der GLeichung x + 5 = 7 ist die Lösungsmenge L = {2}.
Normalerweise ist das bei linearen Gleichungen genau ein Wert.
Definition Grundmenge (G)
Oft steht bei der Aufgabenstellung, dass dieser Wert der Grundmenge (G) entnommen werden muss. Das kann z. B. die Menge der reellen Zahlen sein. Dies wird in der Mathematik so geschrieben: ℝ. Im Beitrag Zahlenmengen habe ich die einzelnen Mengen erklärt.
Definition Definitionsmenge:
Die Definitionsmenge (D) ist die Menge, mit denen die Gleichung durchgeführt werden darf. Z. B. darf man nicht durch Null dividiert.
Definition Äquivalenzumformung:
Die Lösungsmenge einer linearen Gleichung findet man durch Äquivalenzumformung. Äquivalent bedeutet gleichwertig, mit anderen Worten, man darf beide Seiten auf gleiche Weise umformen. Dadurch vereinfacht man die Gleichung.
Erlaubt sind:
- Auf beiden Seiten einer Gleichung die gleiche Zahl oder den gleichen Term addieren oder subtrahieren.
- Beide Seiten einer Gleichung mit der gleichen Zahl, mit demselben Term zu multiplizieren oder durch die gleiche Zahl zu dividieren.
Nicht erlaubt ist:
- Multiplikation mit Null, Division durch Null, sowie quadrieren beider Seiten.
1. Beispiel: Lineare Gleichung, bei der die Variable x auf beiden Seiten vorkommt:
2. Beispiel: Lineare Gleichung mit Formvariablen:
Die Variable u heißt hierbei Parameter oder Formvariable. Die Variable x ist die Lösungsvariable.
Parameter oder auch Formvariable sind hierbei Platzhalter für jeweils ein beliebiges Element aus der Definitionsmenge.
3. Beispiel: Gleichung, mit Brüchen, bei der die Variable x auf beiden Seiten vorkommt.
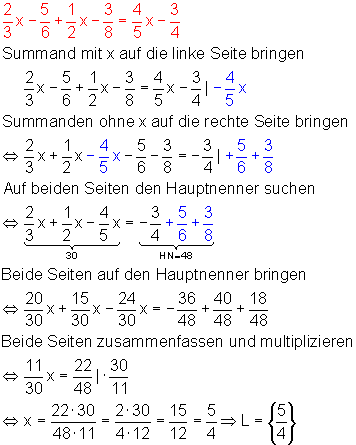
4. Beispiel: Lineare Gleichung mit Klammerausdrücken.
5. Beispiel: Lineare Gleichung mit eckiger und runder Klammer (Zweifachklammerung):
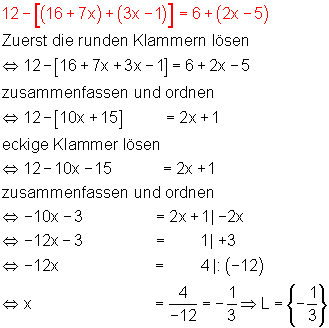
6. Beispiel: Lineare Gleichung mit geschweifter, eckiger und runder Klammer (Dreifachklammerung):
Gleichungen können die Lösungsvariable auch im Nenner enthalten. Solche Gleichungen nennt man dann Bruchgleichungen. Sie lassen sich aber häufig durch Äquivalenzumformungen in linearen Gleichungen umformen.
7. Beispiel: Eine Bruchgleichung wird zur linearen Gleichung:
Bei Bruchgleichungen muss man die Definitionsmenge angeben.
Keine oder unendlich viele Lösungen:
Meistens hat eine lineare Gleichung genau eine Lösung. Aber manchmal gib es keine Lösung oder unendlich viele Lösungen hat.
8. Beispiel: keine Lösung:
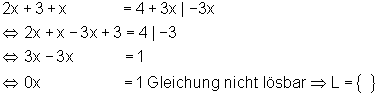
9. Beispiel: unendlich viele Lösungen:
Tipps für Anfänger und Fortgeschrittene:
Anfängern empfehle ich, bei der Lösung linearer Gleichungen in kleinen Schritten vorzugehen. Wer hingegen schon mehr Routine hat, kann auch mehrere Schritte zugleich vornehmen. Hier ein Beispiel dazu:
10. Aufwendiges Beispiel etwas kürzer:
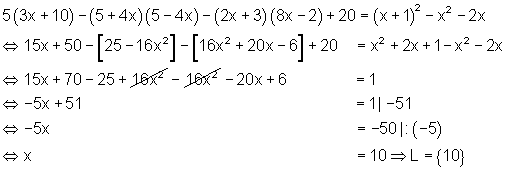
Dazu findest du hier Aufgaben.
Außerdem Aufgaben zu Linearen Gleichungen, Brüchen und Klammern.
