Hier findest du die Lösungen zu Potenzen vereinfachen I mit komplettem Lösungsweg. Zuerst die Lösungen der Aufgaben, in denen Potenzen mit Hilfe der Potenzgesetze vereinfacht werden sollen. Am Schluss Lösungen zu Sachaufgaben aus dem Alltag.
1. Vereinfache folgende Potenzen mit Hilfe der Potenzgeseze!
![]()
![]()
Die ersten beiden Aufgaben kannst du dir in diesem Shorts Potenzen vereinfachen ansehen.
![]()
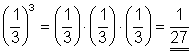
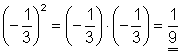
![]()
![]()
![]()
2. Vereinfache!
a)
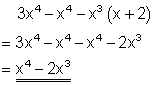
b)
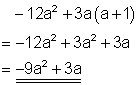
c)
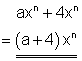
d)
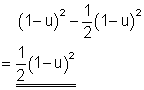
e)
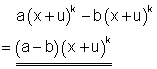
f)
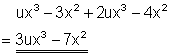
3. Vereinfache!
a)
3a^k \cdot a^{k-1} \cdot a = 3a^{k+k-1+1} = \underline{\underline{3a^{2k}}}
b)
\left(\dfrac{x}{3}\right)^4 \cdot \left(\dfrac{x}{3}\right)^2 = \left(\dfrac{x}{3}\right)^{4+2} = \underline{\underline{\left(\dfrac{x}{3}\right)^6}}
c)
u^3 \cdot u^4 - u^5 (u^2 +1) = u^7 - u^7 - u^5 = \underline{\underline{-u^5}}
d)
x^2 \cdot x^3 \cdot x^4 = x^{2+3+4} = \underline{\underline{x^9}}
e)
a \cdot b^k \cdot a^{2n} \cdot b^{k-3} = a \cdot a^{2n} \cdot b^k \cdot b^{k-3} = a^{1+2n} \cdot b^{k+k-3} = \underline{\underline{a^{2n+1} \cdot b^{2k-3}}}
Diese Aufgabe kannst du dir in diesem Video Potenzen multiplizieren ansehen.
f)
u^2 \cdot x^2 \cdot u^n \cdot x^{n-1} = u^2 \cdot u^n \cdot x^2 \cdot x^{n-1} = u^{2+n} \cdot x^{2+n+1} = \underline{\underline{u^{2+n} \cdot x^{n+1}}}
g)
b^n \cdot b^{2n+1} = b^{n+2n+1} = \underline{\underline{b^{3n+1}}}
h)
(x-2)^n \cdot (x-2)^{1-n} = (x-2)^{n+1-n} = (x-2)^1 = \underline{\underline{x-2}}
i)
(x+1)^{n-1} \cdot (x+1)^{n+1} = (x+1)^{n-1+n+1} = \underline{\underline{(x+1)^{2n}}}
4. Vereinfache!
a)
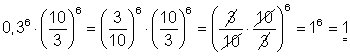
b)
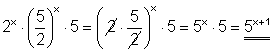
c)
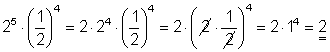
d)
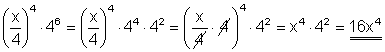
e)
![]()
f)
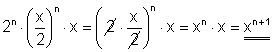
g)
![]()
h)
![]()
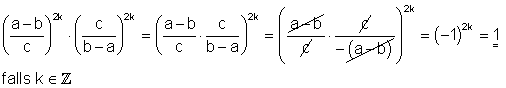
5. Vereinfache mit Hilfe einer Fallunterscheidung.
a)
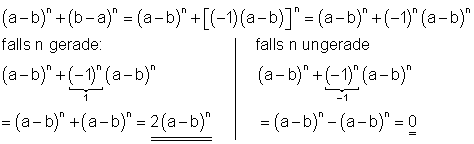
b)
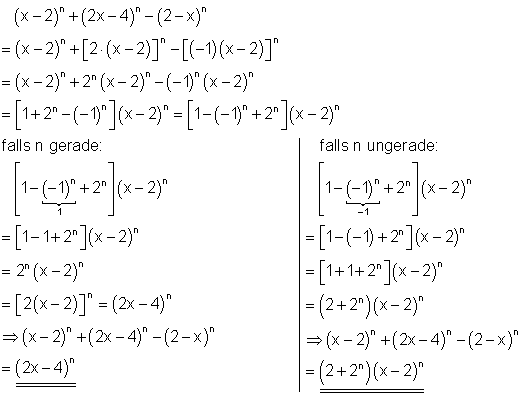
6. Überprüfe folgende Behauptung
![]()
Begründen Sie Ihre Antwort.
Gibt es Zahlen a und b, so dass eine wahre Aussage entsteht?
Lösung:
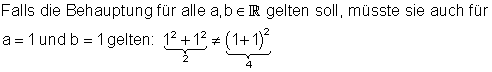
Das ist offensichtlich nicht der Fall.
Die Behauptung gilt nicht für alle a, b.
Es gibt aber Zahlen, die zu einer wahren Aussage führen:
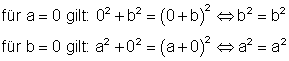
7. Welche Bedingungen müssen a und b erfüllen, damit gilt:
![]()
Lösung:
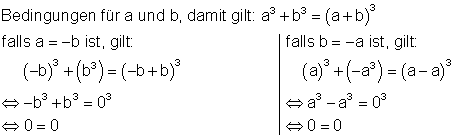
Weitere Lösungen wären, wenn a = 0 und wenn b = 0.
8. Gibt es aufeinanderfolgende natürliche Zahlen
a, b und c, so dass nebenstehende Gleichung gilt?
Falls ja, gib ein Beispiel an.
Durch systematisches Suchen findet man:
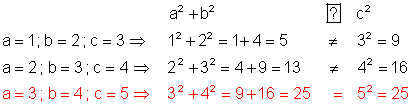
9. Die Bevölkerung eines Staates
wächst um 1,5% pro Jahr. Um wie viel nimmt die Einwohnerzahl bis 2020 zu, wenn die heutige Zahl (2003) 45,6 Millionen beträgt.
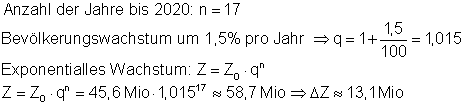
Hier findest du die Aufgaben hierzu
und hier die Theorie: Potenzen, Wurzenl und ihre Rechengesetze.
Hier eine Übersicht über alle Beiträge zu den mathematischen Grundlagen, dort findest du auch viele weitere Aufgaben zu Potenzen.
Dazu kannst auch den Wikipedia-Artikel zu Potenzen lesen.

