Terme in der Mathematik und binomische Formeln

1. Definition Variable:

In der Mathematik nennt man Buchstaben, die als Platzhalter für Zahlen benutzt werden, Variable.
Dabei kann man für diese Buchstaben je nach Situation verschiedene Zahlen einsetzen. Deshalb werden Variable auch Veränderliche genannt. Das ist nützlich, wenn man oft die gleiche Rechnung mit verschiedenen Zahlen durchführt.

Definition Terme:

Ausdrücke, in denen Variable und/oder Zahlen mit Rechenzeichen verbunden werden, heißen Terme.
Den Wert eines Terms errechnet man, wenn man für jede Variable eine Zahl einsetzt.

Beispiel für Terme:

Term: x+5
Variable: x
Wert des Terms bei z.B. x=2
x+5=2+5=\underline{\underline{7}}

Term: x\cdot(x+y)
Variablen: x; y
Wert des Termsbei z.B. x=5 und y=1
x\cdot(x+y)=5\cdot(5+1)=5\cdot6=\underline{\underline{30}}

Was Terme nicht sind:

Terme müssen vollständig sein, außerdem dürfen keine Relationszeichen wie = < > darin vorkommen.

Kein Term sind also z. B.:

x+5 = y , wegen dem =.
x\cdot(x+y) < 5 , wegen dem <. x+ , weil es unvollständig ist.

2. Grundrechenarten in Termen

Man kann mit Termen genauso rechnen wie mit Zahlen. Dabei gelten auch die gleichen Regeln:

Summe von a und b    a+b

Differenz von a und b    a-b

Produkt    3\cdot x=x+x+x

Potenz    x^3=x\cdot x\cdot x

Quotient (Bruch)    \frac{a}{b}~~b\not=0
a : Zähler, b : Nenner

Kehrwert von a :    \frac{1}{a}~~a\not=0

3. Rechengesetze

a) Kommutativgesetz

Wenn man Variablen oder Zahlen addiert oder multipliziert, kann man die Reihenfolge dabei vertauschen. Deshalb nennt man das Kommutativgesetz auch Vertauschgesetz.

Beispiele für das Kommutativgesetz:

a+b=b+a
a\cdot b=b\cdot a

3+5=5+3=\underline{\underline{8}}
15\cdot 5 = 5\cdot 15=\underline{\underline{75}}

b) Assoziativgesetz:

Das Assoziativgesetz bedeutet folgendes:

In Termen, in denen Variablen nur addiert werden,  darf man Klammern beliebig setzten.

In Termen, in denen Variablen nur multipliziert werden,  darf man auch Klammern beliebig setzten.

Achtung: Das gilt nicht, wenn mehrere, verschiedene Rechenoperationen durchgeführt werden!

Dadurch kann man sich das Rechnen erleichtern, z. B. erst Zahlen addieren, deren Summe 10 ergibt.

Beispiele für das Assoziativgesetz

a) a+(b+c)=(a+b)+c
= a+b+c

b) a\cdot(b\cdot c)=(a\cdot b)\cdot c=a\cdot b\cdot c

c) 1+(2+3)=(1+2)+3
=1+2+3=\underline{\underline{6}}

d) 3+(7+5)=(3+7)+5=15

e) 3\cdot(2\cdot 4)=(3\cdot 2)\cdot 4
= 3\cdot 2\cdot 4=\underline{\underline{24}}

c) Distributivgesetz

Das Distributivgesetz bedeutet folgendes:

Statt eine Summe mit einer Zahl zu multiplizieren kann man jeden Summanden mit der Zahl multiplizieren.

💡 Denk daran: Punktrechnung (Multiplikation und Division) geht vor Strichrechnung (Addition und Subtraktion)!

Beispiele für das Distributivgesetz:

a) a\cdot(b+c)=a\cdot b+a\cdot c

b) (a+b)\cdot c=a\cdot c+b\cdot c

c) 2\cdot (3+4)
= 2\cdot 3+2\cdot 4=6+8=\underline{\underline{14}}

d) (2+3)\cdot 4
= 2\cdot 4+3\cdot 4=8+12=\underline{\underline{20}}

Man kann sich das Multiplizieren mit zweistelligen Zahlen erleichtern, indem man die zweistellige Zahl in ein Vielfaches von 10 und eine einstellige Zahl aufteilt. Z. B.:

e) 9\cdot 26 = 9\cdot (20+6)
= 9\cdot 20+9\cdot 6=180+54=\underline{\underline{234}}

Umgekehrt kann man auch statt jeden Summanden mit einer Zahl zu multiplizieren, die Summe mit der Zahl multiplizieren. Das ist z. B. praktisch, wenn die Summe 10 ergibt.

9\cdot 4+9\cdot 6
= 9\cdot (4+6)=9\cdot10=\underline{\underline{90}}

4. Auflösen von Klammern

Klammern löst man von innen nach außen auf.

Vorzeichenregel bei Klammern
Pluszeichen vor der Klammer

Klammern, vor denen ein Pluszeichen steht, kann man dabei einfach weglassen.

Beispiele:

2 + (+3) = 2 + 3 = 5
2 + (-3) = 2 – 3 = -1

Als nächstes ein komplizierteres Beispiel. Versuche einmal alleine, die Lösung zu finden! Wende dabei die Regeln von oben an!

5 + {7 + [2 + (3 - 1)]}
= 5 + {7 + 2 + 3 -1}
= 5 + 7 + 2 + 3 - 1 = \underline{\underline{16}}

Genauso geht man bei Termen vor:
a + [b + (c + d)
= a + [b + c + d]
= a + b + c + d

Minuszeichen vor der Klammer

Wenn man eine Klammer mit einem Minuszeichen davor auflöst, dann muss man die Vorzeichen in der Klammer umdrehen.

Also aus einem Pluszeichen wird dann ein Minuszeichen und aus einem Minuszeichen ein Pluszeichen.

Schauen wir uns erst einmal eine Zahl in der Klammer an.

Beispiel: 2 – (+3)  Hierbei müssen wir die +3 von der 2 subtrahieren. Wenn wir die Klammer auflösen, bleibt also 2 – 3 = -1.

Wir erhalten also das gleiche Ergebnis wie oben mit: 2 + (-3) = 2 – 3 = -1

Beispiel: 2 – (-3) Diesmal müssen wir die -3 von der 2 subtrahieren. Das kann ja nicht das gleiche Ergebnis ergeben wie oben! Deshalb haben wir nach Auflösen der Klammer: 2 + 3 = 5
Das ist etwa so, wie wenn man sagt: ‚Das ist jetzt nicht unwichtig.‘ Das bedeutet ja so viel wie: ‚Das ist jetzt wichtig.‘ Eine doppelte Verneinung ist eine positive Aussage. Genauso werde in der Mathematik aus zwei Minuszeichen ein Pluszeichen. Wir können uns auch merken:

Treffen gleiche Vorzeichen aufeinander, so entsteht ein Pluszeichen.

Treffen ungleiche Vorzeichen aufeinander, so entsteht ein Minuszeichen.

Das gleiche gilt bei der Multiplikation:

Pluszeichen vor der Klammer:
a) 2\cdot (+3) = 2\cdot +3 = \underline{\underline{6}}

b) -2\cdot (+3) = -2\cdot 3 = \underline{\underline{-6}}

Minuszeichen vor der Klammer:

c) 2\cdot (-3) = 2\cdot -3 = \underline{\underline{-6}}

d) -2\cdot (-3) = -2\cdot -3 = \underline{\underline{6}}

e) 5 - {7 - [2 + (3 - 1)]}
= 5 - {7 - [2 + 3 -1]} = 5 - {7 - 2 - 3 +1}
= 5 - 7 + 2 +3 -1 = \underline{\underline{2}}

Genauso verfährt man mit Termen:

a - [b - (c - d)]
= a - [b - c +d]
= a - b + c -d

5. Terme zusammenfassen

Wenn man einen Term mit mehreren Variablen hat, ist es sinnvoll, nach Variablen zu ordnen. Danach kann man nämlich gleiche Variablen zusammenfassen.

Hier zum Beispiel haben wir mehrere x- und y-Variablen in einem Term:
32x + 12y - 4x -5y -14x + 2y
Zuerst ordnen wir:
= 32x - 4x - 14x + 12y - 5y + 2y
Danach können wir gleiche Variablen leichter addieren bzw. subtrahieren:
= \underline{\underline{14 x + 9y}}

Beachte bei den nächsten Beispielen die Klammerregeln!

3a + (4a - 2b) - 8(b - a)
= 3a + 4a - 2b - 8b + 8a
= 3a + 4a + 8a - 2b - 8b = \underline{\underline{15a - 10b}} 

Beachten Sie dabei die Rechenzeichen vor der Klammer!

Klammern auflösen bei Multiplikation

Wenn wir in einer Klammer eine Summe oder eine Subtraktion haben und diese Klammer mit einem Faktor multipliziert wird, müssen wir anders vorgehen. Dann müssen wir jedes Glied in der Klammer mit dem Faktor multipliziert.

Dies gilt, wenn wir mit einer Zahl multiplizieren:

3(2x - 4y) - 4(3 - 4x - 2y)
= 6x - 12y - 12 + 16 x + 8y
= \underline{\underline{22x - 4y - 12}}

Und auch, wenn wir mit einer Variablen multiplizieren:

8xy \cdot(-3x)
= 8 \cdot x  \cdot y \cdot(-3x)  = \underline{\underline{-24x^2y}}

Dabei dürfen wir die Faktoren vertauschen:

9a - [5a - (b - 8a)]
= 9a - [5a - b + 8a] = 9a - 5a + b - 8a = 9a - 5a - 8a + b
= \underline{\underline{-4a +b}}

In diesem  shorts erkläre ich eine Aufgabe dazu.

Termvereinfachung durch ausklammern

Manchmal will man Terme in Klammern zusammenfassen, um sie übersichtlicher zu gestalten.
Hierzu zerlegt man alle Summanden in Faktoren.
Dann klammert man den größten gemeinsamen Faktor aus.

Ausklammern macht aus einer Summe ein Produkt, mit anderen Worten: diesen Vorgang nennen wir faktorisieren.

Beispiele:

a) 27x - 27
Hier haben wir zweimal die Zahl 27. Es drängt sich also auf, eine Klammer zu bilden:
{\color{red}{27}}x - {\color{red}{27}} \cdot 1 =\underline{\underline{{\color{red}{27}}(x - 1)}}

b) 8x + 24
Hier müssen wir den größten gemeinsame Faktor suchen. Der ist in diesem Fall 8. Deshalb können wir so zusammenfassen:
={\color{red}{8}}x + {\color{red}{8}} \cdot 3 = \underline{\underline{8(x + 3))}}

c) {\color{blue}15x + 9y - 21}
Hier ist der größte gemeinsame Faktor 3:
{\color{red}{3}} \cdot 5x + {\color{red}{3}} \cdot 3y - {\color{red}{3}}\cdot 7
= \underline{\underline{{\color{red}{3}}(5x + 3y - 7)))}}
Zur Sicherheit führen wir eine Probe durch ausmultiplizieren durch:
3(5x + 3y - 7) = \underline{\underline{{\color{blue}15x + 9y - 21}1}}

Terme mit Brüchen zusammenfassen:

d) - \frac{3}{4}x^2 +\frac{5}{8}x - 3
Als erstes müssen wir die Brüche erweitern, um sie gleichnamig zu machen:
= -\frac{6}{8}x^2 + \frac{5}{8}x - \frac{24}{8}
Als nächstes können wir den Bruch als Faktor ausklammern:
= \underline{\underline{- \frac{1}{8} (6x^2 - 5x +24)}}

e) -\frac{3}{5} - x + \frac{8}{5}y
= -\frac{3}{5} - \frac{5}{5}x + \frac{8}{5}y
= \underline{\underline{-\frac{1}{5}(3 + 5x - 8y)}}

f) In der folgenden Aufgabe sind a und m zur Verdeutlichung farblich hervorgehoben. Außerdem habe ich die Multiplikationspunkte eingezeichnet, obwohl sie nicht nötig sind.

In der ersten Hälfte des Terms können wir a, in der zweiten m ausklammern.

Um den nächsten Schritt zu erleichtern, können wir in Gedanken die Summe (b +c) durch ein d ersetzen. Dann sehen wir, dass a und m mit d multipliziert werden. Deshalb können wir das faktorieren:

g) - {\color{red}{6a}} m + {\color{red}{12a}} n - {\color{red}{2a}} p + {\color{blue}{3b}}m - {\color{blue}{6b}}n + {\color{blue}{b}} p
Hier gehen wir ähnlich vor wie in der Aufgabe zuvor. Im ersten Teil des Terms haben wir ein Mehrfaches von a. Zusätzlich suchen wir den größten Faktor dazu. Das ist hier die 2. Also können wir 2a ausklammern.

Im zweiten Teil des Terms können wir nur b ausklammern.

= - {\color{red}{2a}} (3m - 6n + p) + {\color{blue}{b}} (3m - 6n + p)
Der Inhalt der Klammer (3m – 6n + p) wird sowohl mit 2a also auch mit b multipliziert. Deshalb können wir dies auch ausklammern:

6. Summen multiplizieren

Summen ausmultiplizieren, anders ausgedrückt: jeden Summanden der einen Summe mit jedem Summanden der anderen Summe multiplizieren.

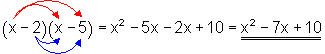
In diesem Beispiel habe ich farbig markiert, was womit multipliziert wird.
Rote Pfeile: Wir multiplizieren das x aus der ersten Klammer mit beiden Elementen aus der zweiten Klammer.
Blaue Pfeile: Wir multiplizieren die Minus 2 aus der ersten Klammer mit beiden Elementen aus der zweiten Klammer. Dabei dreht sich das Vorzeichen um.
Im letzten Schritt fassen wir zusammen.

Beispiele:

a) (2x -3) (1 - tx)
= 2x - 2tx^2 - 3 + 3tx
= \underline{\underline{-2tx^2 + 3tx + 2x - 3}}

Beim nächsten Beispiel multiplizieren wir drei Klammern. Das geht einfach, wenn wir als erstes die ersten beiden Klammern multiplizieren. Danach dann die dritte. Am Ende sortieren und fassen wir zusammen:
b) (x - 2) (x - 3) (2x +1)
= (x^2 - 3x - 2x + 6) ( 2x + 1)
= (x^2 - 5x + 6) ( 2x + 1) \\ = 2x^3 + x^2 - 10x^2 - 5x + 12x + 6 \\ = \underline{\underline{2x^3 - 9x^2 + 7x + 6}}

c) (x - y) ( 3 - 2a)
= \underline{\underline{-3x - 2ax - 3y + 2ay}}

d) (2x - 7) ( 3x + 4)
= 6x^2 + 8x - 21x - 28
= \underline{\underline{6x^2 - 13 x - 28}}

e) (a + b) (a - b)
= a^2 - ab - ba - b^2
= a^2 - ab + ab - b^2 = \underline{\underline{a^2 - b^2}}

7. Binomische Formeln

Binomische Formeln sind ein Sonderfall bei der Multiplikation von Summen. Dabei haben wir in zwei Klammer je zwei gleiche Elemente, die multipliziert werden. Wenn wir dies sehen, brauchen wir nicht lange überlegen und können sofort ausklammern. Da das häufig auftritt, erspart wir uns dadurch viel Arbeit.
Es gibt drei von ihnen:

1. Binomische Formel:

Die Erklärung hierfür leuchtet ein, wenn wir uns klar machen:
= (a + b)^2 = (a + b) (a + b)

2. Binomische Formel:

Hierbei müssen wir beachten, dass die Multiplikation zweier negativer Werte einen positiven Wert ergeben:
= (a - b)^2 = (a - b) (a - b)

3. Binomische Formel:

(a + b) (a - b) = a^2 - b^2
Diese Aufgabe haben wir oben unter e) bereits berechnen. Wenn wir jedes Element aus der ersten Klammer mit jedem aus der zweiten Klammer multiplizieren wird klar, dass sich ab aufhebt:
= a^2 - ab + ab - b^2

Beispiele für binomische Formeln:

a) (x + 2)^2 = \underline{\underline{x2 + 4x + 4}}

b) (x - 3)^2 = \underline{\underline{x^2 - 6x + 9}}

c) (x + 4) (x -4) = \underline{\underline{x^2 - 16}}

d) (3x + 2y)^2 = \underline{\underline{9x^2 + 12xy + 4y^2}}

e) (2x - 3y)^2 = \underline{\underline{4x^2 - 12xy + 9y^2}}

f) (4x + 3y) (4x - 3y) = \underline{\underline{16x^2 - 9y^2}}

Term in binomische Formel umwandeln

Manchmal lohnt es sich, den umgekehrten Weg zu gehen. Dazu schaut man, ob ein Term aus zwei Additionen besteht, bei denen der erste und letzte Werte ein Zweierpotenz sind. Außerdem muss der mittlere Wert ein entsprechendes Produkt sein.

Beispiele fürs Rechnen mit binomischen Formeln

a) 4x^2 + 12xy + 9y^2
= (2x) + 2 \cdot 2x  \cdot3y \\ = (2x + 3y)^2

b) 9a^2 - 6ab + b^2
= (3a)^2 - 2 \cdot 3 \cdot  a \cdot  b + (b)^2 \\ = (3a - b)^2

c) m^2 + 2m + 1 \\ = (m)^2 + 2 \cdot m \cdot 1 \\ = (m + a)^2

Hier gibt es Aufgaben zu Terme und Binomische Formeln.
Und hier: Terme Aufgaben II mit binomischen Formeln.
Und hier: Terme Aufgaben III mit binomischen Formeln.

Die vier Grundrechenarten

Kopfrechenübungen der vier Grundrechenarten mit unterschiedlichen Schwierigkeitsgraden

Kopfrechenübungen