In diesem Beitrag erkläre ich mehrere, einfache Wege, Bruchgleichungen zu lösen. Dazu werde ich viele Beispiele vorstellen.
- Bevor man Bruchgleichungen löst, muss man immer erst die Definitionsmenge bestimmen.
- Anschließend werde ich den Trick mit der Kehrwertbildung
- und mit der Multiplikation über Kreuz vorstellen.
- Schließlich werde ich einen simplen Beweis für die Gültigkeit der Kehrwertbildung zeigen.
- Zuletzt verlinke ich zu Aufgaben und weiteren Beiträgen.
Definitionsmenge von Bruchgleichungen
Die Grundmenge einer Bruchgleichung ist, falls nichts anderes angegeben wird, IR. Die Definitionsmenge enthält also die Variabelenwerte, für die die Gleichung gültig ist. Zur Bestimmung der Definitionsmenge muss man untersuchen, für welche Variabelenwerte der Nenner Null wird. Man bestimmt also die Nennernullstellen. Genau diese Werte gehören nicht zur Definitionsmenge.
1. Beispiel:

2. Beispiel:
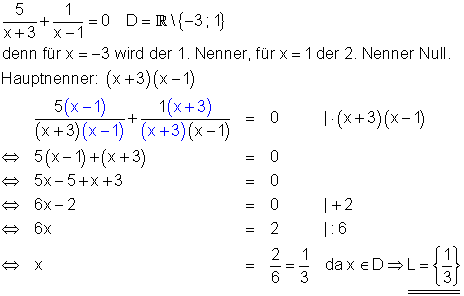
3. Beispiel:
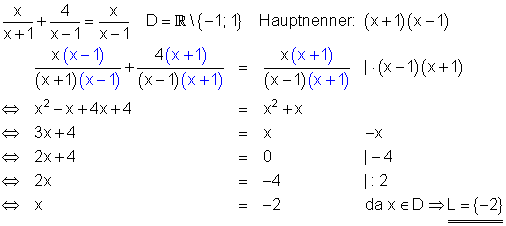
Nachdem beide Seiten der Bruchgleichung auf den Hauptnenner gebracht wurden, führt die anschließende Multiplikation mit dem Hauptnenner dazu, dass keine Brüche mehr vorhanden sind.
4. Beispiel:
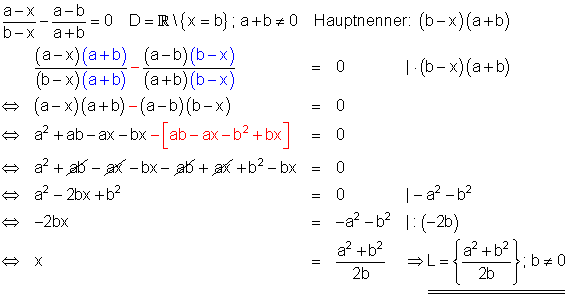
Besteht die rechte Seite der Bruchgleichung nur aus dem Wert Null, so bringt man die linke Seite auf den Hauptnenner. Die Multiplikation mit dem Hauptnenner führt auch hier dazu, dass keine Brüche mehr vorhanden sind. Zu berücksichtigen ist aber, dass der Bruchstrich eine Klammer ersetzt. Steht vor einem Bruch ein Minuszeichen, so ist nach Wegfall der Brüche der entsprechende Zählerterm in eine Minusklammer zu setzen.
Der Trick mit der Kehrwertbildung bei Bruchgleichungen

Dies kannst du dir in diesem 
In manchen Fällen kann die Berechnung der Bruchgleichung durch eine Kehrwertbildung vereinfacht werden.
Das gilt insbesondere dann, wenn die Zähler der Brüche nur aus Zahlen bestehen.
Der Trick mit der Multiplikation über Kreuz bei Bruchgleichungen

Die Berechnung der Bruchgleichung kann durch eine kreuzweise Multiplikation ebenfalls verkürzt werden.
Dabei wird der Nenner des ersten Bruchs mit dem Zähler des zweiten multipliziert und der Nenner des zweiten mit dem Zähler des ersten.
Das ist aber nur dann möglich, wenn die Bruchgleichung die nebenstehende Form besitzt.
Simpler Beweis für die Gültigkeit der Kehrwertbildung bei Bruchgleichungen

5. Beispiel:
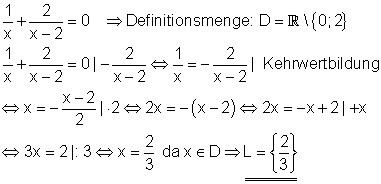
6. Beispiel:
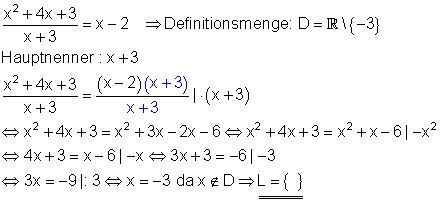
Dieses Beispiel zeigt, wie wichtig es ist, die Definitionsmenge der Bruchgleichung zu bestimmen. Die Äquivalenzumformung führt zwar zu einem Ergebnis, doch die Ausgangsgleichung ist für diesen Wert nicht definiert.
7. Beispiel:
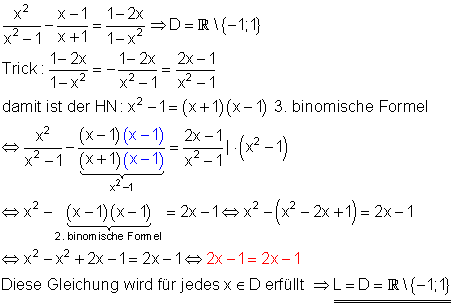
Diese Bruchgleichung hat unendlich viele Losungen, denn die Gleichheitsbedingung ist für jedes x der Definitionsmenge erfüllt.
Dazu findest du hier die Aufgaben Bruchgleichungen.
Und Aufgaben Bruchungleichungen IAufgaben zu Lineare Gleichungen mit Brüchen und Klammern.
Außerdem hier Aufgaben Lineare Gleichungen mit Sach- und Textaufgaben.
Hier findest du eine Übersicht über alle Beiträge zum Thema Gleichungen, darin auch Links zu weiteren Aufgaben.
Außerdem kannst du den Wikipediaartikel zu Bruchgleichungen lesen.
Schließlich findest du hier die Playlist aller Videos zu linearen Gleichungen.

