Hier findest du Aufgaben mit Bruchgleichungen.
Definitionsmenge bestimmen und Gleichung lösen
Zuerst möchte ich eine Hilfestellung zur Definitionsmenge geben:
Hier einige Tipps zum lösen von Bruchgleichungen: Die Definitionsmenge enthält alle Werte der Variablen x, für die die Gleichung gültig ist. Da der Nenner eines Bruches nie Null werden darf, ist zur Bestimmung der Definitionsmenge zu untersuchen, für welche Werte der Variablen x der Nenner Null wird.
Und Beispiele für die Definitionsmenge von Bruchgleichungen:
Beispiel 1:
Die Bruchgleichung ist gültig für alle Werte der Variablen x, außer der Null.
Beispiel 2:
Die Bruchgleichung ist gültig für alle Werte der Variablen x, außer der 7. Denn für x = 7 wird der Nenner Null.
Beispiel 3:
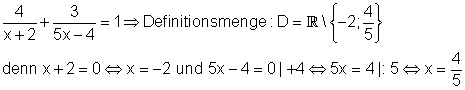Im 1. Bruch wird der Nenner für x = -2 Null. Im 2. Bruch wird der Nenner für x = 4/5 Null. Der Trick mit der Multiplikation über Kreuz: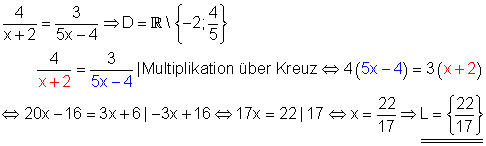 
Dabei können dir diese Videos helfen:
Video Lineare Gleichung mit Brüchen lösen1. Aufgabe: Bestimme die Definitionsmenge und löse die Gleichungen.
a) 
b) 
c) 
e) 
f) 
g) 
h) 
i) 
2. Bestimme die Definitionsmenge
und löse die Gleichungen. a) 
b) 
c) 
d) 
e) 
f) 
3. Überprüfe folgende Behauptung!
4. Bestimme die Definitionsmenge
und löse die Gleichungen. a) 
b) 
5. Zeige, dass folgendes gilt:
6. Löse das Gleichungssystem:
7. LKW
Ein kleiner LKW fährt einen Aushub von 405 m3 in x Fahrten zur Deponie. Ein großer LKW braucht dazu 9 Fahrten weniger. Zusammen schaffen beide LKW’s den Aushub in je 20 Fahrten. Wie viel Fahrten braucht jeder LKW alleine und welche Ladekapazität hat jeder?
8. Zahl
Welche natürliche Zahl(en) kann man zum Zähler von 2/5 addieren und gleichzeitig vom Nenner subtrahieren um -2 zu erhalten?
9. Bestimme die Definitionsmenge
a) Bestimme die Definitionsmenge und die Lösungsmenge. b) Ersetze 3/2 durch eine andere Zahl so, dass die sonst unveränderte Gleichung die Lösung x = – 1 hat.
Dazu findest du hier die Lösungen.
Und hier die Theorie Lösen von Bruchgleichungen.
Außerdem kannst du den Wikipediaartikel zu Bruchgleichungen lesen.
Hier findest du eine Übersicht über alle Beiträge zum Thema Gleichungen, dort auch Links zu weiteren Aufgaben.
