Polynomgleichungen einfach erklärt

Definition und Beispiel Polynomgleichung

Verschiedene Potenzen von x auf der linken und rechten Seite einer Gleichung ergeben eine Polynomgleichung.

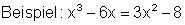
Lösungsverfahren für Polynomgleichung: in die Nullform, Normalform bringen

Um eine solche Gleichung zu lösen, bringt man sie zunächst auf die sogenannte Nullform. Das heißt, die Gleichung wird solange mittels Äquivalenzumformung bearbeitet, bis auf der rechten Seite nur noch die Null steht.

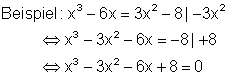
Statt Nullform sagt man zu dieser Form der Polynomgleichung auch Normalform.

Dazu kannst du dir dieses 📽️ Shorts Polynomgleichung, Normalform Was ist das? ansehen.

Man unterscheidet mehrere Varianten von Polynomgleichungen, für die es unterschiedliche Lösungsverfahren gibt. Um die jeweilige Variante zu erkennen, ist es erforderlich, die Polynomgleichung wie oben beschrieben, auf die Nullform zu bringen.

1. Beispiel: Polynomgleichung mit nur einer einzige Potenz der Variablen x:

Falls n ungerade ist, darf der Radikand auch negativ sein.
Es gibt genau eine Lösung der Wurzel.
Falls n gerade ist, darf der Radikand nur positiv sein.
Es gibt zwei Lösungen.

Beispiele:

Exponent n ungerade und der Radikand negativ:

8x^3 = -27 | :8
\Leftrightarrow x^3 = -\dfrac{27}{8} | \sqrt[3]{}
\Leftrightarrow x = \sqrt[3]{-\dfrac{27}{8}} = -\dfrac{3}{2} \Rightarrow \underline{\underline{L = \{-\dfrac{3}{2}\}}}

Es gibt nur eine Lösung, denn eine negative Zahl dreimal multiplizieren, ergibt eine negative Zahl. Das gleiche gilt für alle ungeraden Zahlen.

Dazu kannst du dir dieses 📽️ Video Polynomgleichung, 1 Potenz, Exponent ungerade, Radikand negativ ansehen.

Exponent n gerade und der Radikand positiv:

81x^4 = 16 | : 81 
\Leftrightarrow x^4 = \dfrac{16}{81} | \sqrt[4] 
\Leftrightarrow x_{1,2} = \pm \sqrt[4]{\dfrac{16}{81}} = \pm \dfrac{2}{3}  
x_1 = \dfrac{2}{3}  
x_2 = -\dfrac{2}{3}  
  \underline{\underline{L = \{-\dfrac{2}{3} ; \dfrac{2}{3}}}\}

Dazu kannst du dir dieses 📽️ Video Polynomgleichung, 1 Potenz, Exponent gerade, Radikand positiv ansehen.

Wenn der Radikand negativ wäre, kann man die Wurzel und damit die Gleichung nicht lösen. Denn eine negative Zahl viermal multiplizieren, ergibt eine positive Zahl. Das gleiche gilt für alle geraden Zahlen.

2. Beispiel: Polynomgleichung stellt eine quadratische Gleichung dar:

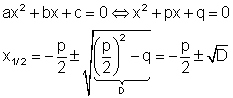
Deshalb lässt sie sich mithilfe der p-q-Formel berechnen. Dazu kannst du dir die Videos 📽️p-q-Formel einfach erklärt (die Theorie) und 📽️quadratische Gleichung lösen mit p-q-Formel Aufgabe anschauen.

Beispiel:

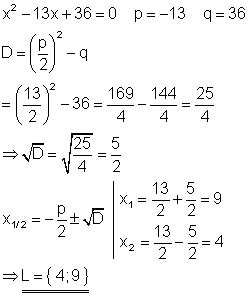
D steht dabei für Diskriminante, anhand der man die Anzahl der Lösungen schon vor der entgültigen Berechnung bestimmen kann.
Wenn D > Null: Die quadratische Gleichung hat 2 Lösungen.
Falls D = Null: Die quadratische Gleichung hat nur eine Lösung ( -p/2 ).
Wenn D < Null: Die quadratische Gleichung hat keine Lösung.
In diesem Fall braucht man an dieser Stelle nicht weiterrechnen.

3. Die Polynomgleichung stellt eine biquadratische Gleichung dar:

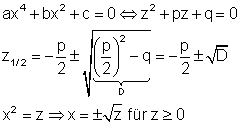
Die Substitutionsvariable z lässt sich mithilfe der p-q-Formel berechnen.
Anschließend muss zurücksubstituiert und die Wurzel gezogen werden.
Die Wurzel lässt sich nur für positive z-Werte lösen.

Beispiel:

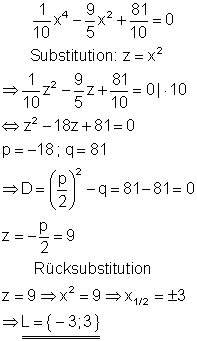
In diesem Fall ist die Diskriminante Null, so dass es für die Substitutionsvariable nur einen Wert gibt (z = 9).
Das bedeutet, die Polynomgleichung 4. Grades hat nur zwei Lösungen.

Dazu kannst du dir dieses 📽️ Video Polynomgleichung lösen, die eine biquadratische Gleichung ist ansehen. 

4. Beispiel: In der Polynomgleichung kommt kein absolutes Glied vor

Es gibt keine alleine stehende Zahl wie z. B. 14. Mit anderen Worten, es gibt  nur Werte, die mit einer Potenz von x multipliziert werden. Deshalb kann man x ausklammern.

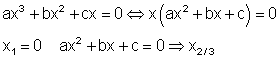
Als erstes klammern wir x aus. Dann haben wir sofort die erste Lösung x = 0. Denn wenn x Null ist, ist das Ergebnis auch Null. Das sagt auch der  Satz vom Nullprodukt: Ein Produkt ist genau dan Null, wenn mindestens ein Faktor Null ist.

Der zweite Faktor (der Ausdruck in Klammern) vom Nullprodukt ist eine quadratische Gleichung, die sich leicht mit der p-q-Formel lösen lässt.

Beispiel:

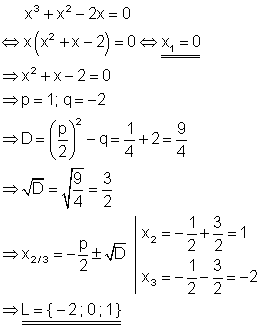
Dazu kannst du dir dieses 📽️ Video Polynomgleichung lösen, die kein absolutes Glied enthält ansehen. 

5. Beispiel: Die Polynomgleichung entspricht nicht einer der Varianten 1 bis 4

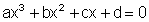
In vielen Fällen lässt sich die Lösung durch die Polynomdivision finden.
Dazu muss aber eine Lösung bekannt sein.Ist eine Lösung des Polynoms bekannt, dann kann der Grad des Polynoms durch Polynomdivision um eins verringert werden. Wenn das auf eine quadratische Gleichung führt, ist es ein leichtes, die weiteren Lösungen zu finden.
Folgendes Beispiel, bei dem die Lösung x = 2 bekannt ist soll das Verfahren der Polynomdivision verdeutlichen.
Die Division erfolgt nach den bekannten Regeln der schriftlichen Division.

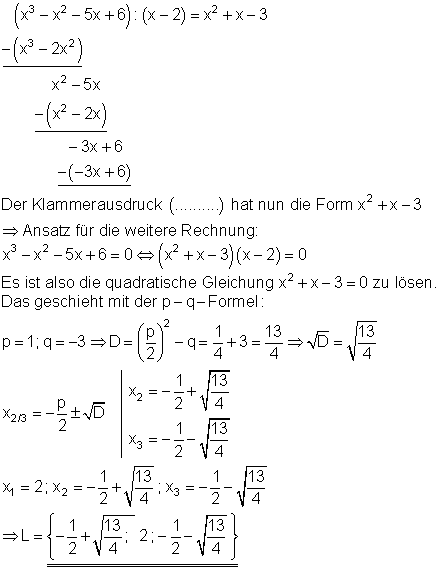
Falls sich keine Lösung, z,B. durch raten oder probieren finden lässt, müssen numerische Verfahren herangezogen werden.