Schnittpunkt von Parabel und Gerade • 123mathe

Hier stelle ich zuerst ein Beispiel aus der Praxis für den Schnittpunkt von Parabeln und Gerade vor. Danach erkläre ich wie man die Funktionsgleichung aufstellt und die Schnittpunkte berechnet. Anhand von Trainingsaufgaben, erkläre ich anschließend die Begriffe Sekante, Tangente und Passante. Außerdem stelle ich einen interaktiven Rechner zur Verfügung.

Beispiel:

Ein Fußweg verläuft unterhalb einer Hochstraße parallel zu ihr.
Jetzt soll am Fuß einer Brücke mit parabelförmigen Bogen der Fußweg in Form einer Rampe errichtet werden, die zur Straße hinaufführt.
Ermittele die Höhe der Stützpfeiler für die Rampe!
Von der Parabel ist lediglich bekannt, dass sie den Formfaktor a₂ = -1/20 besitzt.

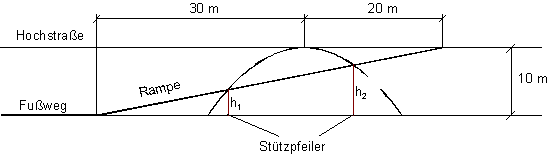
Modellierung

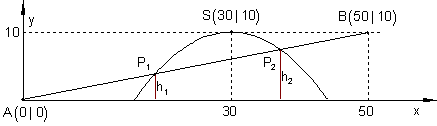
Funktionsgleichungen aufstellen

Was haben wir?
Eine Gerade durch 2 Punkte A(0|0) und B(50| 0) . Außerdem eine Parabel mit Scheitelpunkt S(30|10) und Formfaktor -1/20.

Was suchen wir?
Die Höhe h1 und h2. Das sind die y-Werte der Schnittpunkte.

Was brauchen wir?
Die Lineare Funktion der Geraden und die quadratische Funktion der Parabel.
Die Steigung einer Geraden aus 2 Punkten berechnet man wie folgt:
$a_1 = \dfrac {y_2 - y_1}{x_2 -x_1} = \dfrac {10 - 0}{50 - 0} = \frac{1}{5}$
Weil die Gerade durch den Ursprung des Koordinatensystems verläuft, ist sie nicht verschoben: $g(x) = \frac{1}{5}x$

Aus dem Scheitelpunkt und dem Formfaktor können wir die Scheitelpunktform der Parabel konstruieren:
$f(x) = -\frac{1}{20} (x - 30)^2 + 10$ | 2. binomische Formel auflösen und jeden Summanden mit $-\frac{1}{20}$ multiplizieren
$\Leftrightarrow f(x) = -\frac{1}{20}x^2 + 3x - 35$

Damit wir die Höhe der Stützpfeiler erhalten, benötigen wir die Schnittpunkte der Geraden mit der Parabel.
Dazu kannst du dir das 📽️Video Textaufgabe Schnittpunkt Parabel Gerade Lösungsansatz ansehen.

Schnittpunkte von Parabel und Gerade berechnen

Wir setzen die beiden Funktionen gleich bzw. subtrahieren, damit sich 0 ergibt.
$f(x) = g(x) \Leftrightarrow f(x) - \color{blue}{g(x) = 0}$
$-\frac{1}{20}x^2 + 3x - 35 \color{blue}{-\frac{1}{5}x} \color{black}{= 0}$ | Koeffizienten von x zusammenfassen und Bruch erweitern
$\Leftrightarrow -\frac{1}{20}x^2 + \frac{14}{5}x - 35 = 0 \quad| \cdot (-20)$
$\Leftrightarrow x^2 -56x +700 = 0$
$\Rightarrow p = -56; q = 700$
$\Rightarrow D = (\frac{p}{2})^2 - q = (-28)^2 - 700 = 84$
$x_{1,2} = -\frac{p}{2} \pm \sqrt D$
$\Rightarrow x_1 = 28 + \sqrt {84} \quad \lor \quad x_2 = 28 - \sqrt {84}$
$y_1 = g(x_1) = g(28 + \sqrt{84}) = \frac{1}{5} (28 + \sqrt{84}) \approx \underline{\underline{ 7,433}}$
y_2 = g(x_2) = g(28 - \sqrt{84}) = \frac{1}{5} (28 - \sqrt{84}) \approx \underline{\underline{ 3,767}}

Der Pfeiler h₁ hat die Höhe 3,764 m, der Pfeiler h₂ hat die Höhe 7,433 m.

Wenn wir den Schnittpunkt einer Geraden mit einer Parabel bestimmen, führt das immer auf eine quadratische Gleichung.
Dazu kannst du dir das 📽️Video Schnittpunkt Parabel und Gerade berechnen ansehen.

Aufgaben, Sekante, Tangente und Passante

Bestimme die Schnittpunkte von f(x) mit g(x). Zeichne danach beide Graphen in ein Koordinatensystem!
Benutze für die Zeichnung der Parabel die Scheitelpunktform.

Interaktiver Rechner: Schnittpunkt von Parabel und Gerade
Gib die Koeffizienten beider Funktionsgleichungen ein. Danach berechnet das Javascript die Schnittpunkte und zeichnet beide Graphen.

Lösungen:

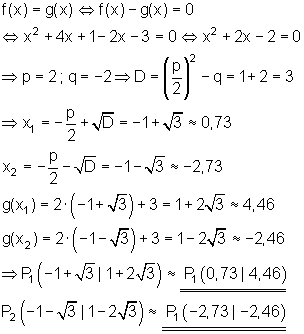
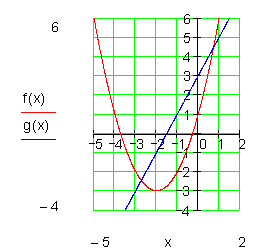
Die Gerade g(x) schneidet den Graphen von f(x) also in zwei Punkten.
Man nennt sie Sekante.

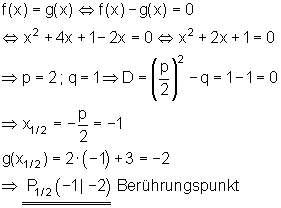
Eine Gerade, die einen Graphen in genau einem Punkt berührt, nennt man Tangente.

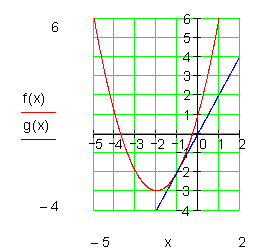
Die Gerade g(x) berührt den Graphen von f(x) folglich in einem Punkt.

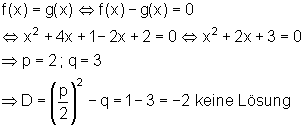
Die Gerade g(x) hat mit dem Graphen von f(x) also keinen Punkt gemeinsam.
Eine solche Gerade nennt man Passante.

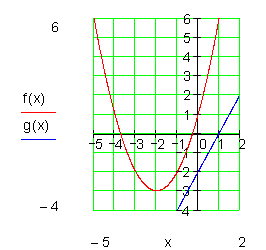
Aus dem Übungsbeispiel erkennen wir, das die Anzahl der Schnittpunkte, die eine Gerade mit einer Parabel hat direkt aus der Diskriminante ablesbar ist.