Im letzten Beitrag ging es um den Schnittpunkt von Parabel und Gerade. Zuerst erkläre ich anhand eines Beispiels, wie man den Schnittpunkt zweier Parabeln berechnet. Anschließend stelle ich Übungsaufgaben hierzu und einen interaktiven Rechner zur Verfügung. Zuletzt erläutere ich dies.
Beispiel zum Schnittpunkt zweier Parabeln
Diesmal wollen wir die Schnittpunkte zweier Parabeln bestimmen und wir haben dafür deren Funktionsgleichungen.
f(x)= x^2 - 4x +1 \, bzw. \, f(x) \\ = (x - 2)^2 - 3 \Rightarrow S(2|-3)
g(x) = -x^2 + 2x + 1 \, bzw. \, g(x) \\ = -(x-1)^2 + 2 \Rightarrow S(1|2)
Wenn der Schnittpunkt der Graphen zweier Funktionen bestimmt werden soll, dann setzt man die Funktionsgleichungen gleich. Das galt schon für die Schnittpunkte von Geraden und ebenfalls von Gerade und Parabel. Deshalb wendet man dieses Verfahren auch bei zwei Parabeln an.
f(x) = g(x) \Leftrightarrow f(x) - g(x) = 0
\Leftrightarrow x^2 - 4x + 1 + x^2 -2x -1 =
0 \\ \Leftrightarrow 2x^2 - 6x = 0 \, \big \vert :2
\Leftrightarrow x^2 - 3x = 0
x(x-3) = 0
\Rightarrow x_1 = 0
x(x-3) = 0 \Rightarrow x_2 = 3
f(x_1) = f(0) = 1
f(x_2) = f(3) = -2
\Rightarrow \underline{\underline{P_1(0|1) ; P_2(3|-2)}}
Aufgaben
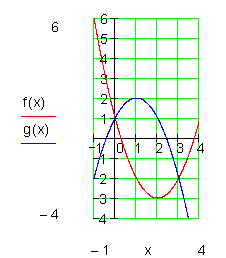
Jetzt kannst du üben: Bestimme die Schnittpunkte folgender Parabeln. Zeichne danach die Graphen!
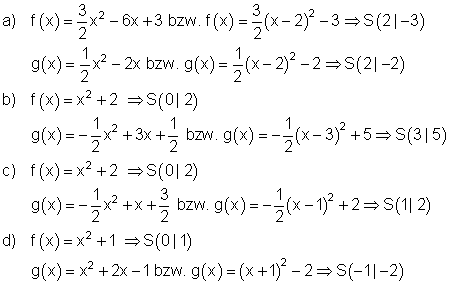
Schnittpunkt zweier Parabeln Interaktiver Rechner:
Gib die Koeffizienten beider Funktionsgleichungen ein. Danach berechnet das Javascript die Schnittpunkte. Außerdem zeichnet es die beiden Graphen.
a)
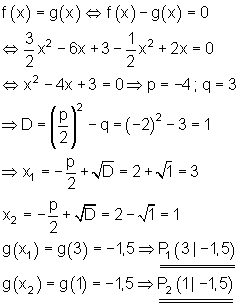
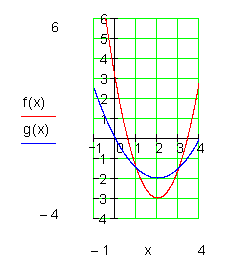
Wir sehen also, dass es zwei Schnittpunkte gibt, denn D> 0.
b)
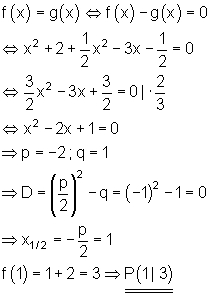
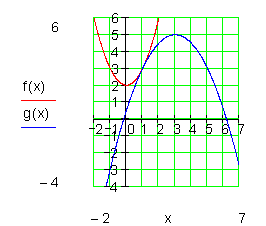
Außerdem es gibt nur einen Berührungspunkt, denn D = 0.
c)
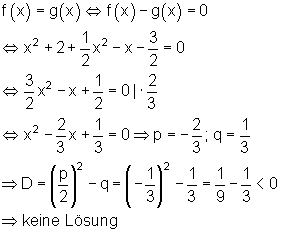
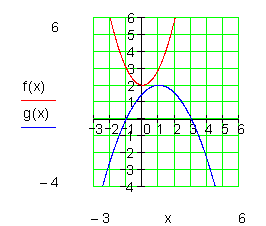
Hier gibt es keinen Schnittpunkt, denn D < 0.
d)
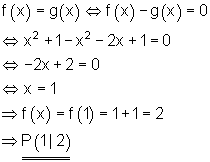
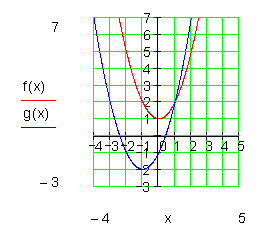
Wenn das Gleichsetzen von f(x) und g(x) auf eine lineare Gleichung führt, haben beide Parabeln nur einen Schnittpunkt.
Die Anzahl der Schnittpunkte, die zwei Parabeln miteinander haben, ist folglich direkt aus der Diskriminante ablesbar.

Im nächsten Beitrag geht es darum, wie man die Funktionsgleichung für eine quadratische Funktion aufstellt, wenn man drei ihrer Punkte kennt.
Dazu findest du hier eine Übersicht über weitere Beiträge zu Quadratischen Funktionen, darin auch Links zu Aufgaben.


