Aufgaben Parabel und Gerade I

Hier findest du Aufgaben, in denen zu die Schnittpunkte von Parabel und Gerade berechnen sollst.

1.

Gegeben ist die Funktionsgleichung einer Parabel mit f(x) und die Funktionsgleichung einer Geraden mit g(x). Berechne die Schnittpunkte.
a)

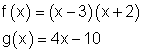
b)

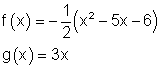
c)

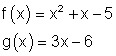
d)

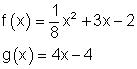
2.

Eine Parabel mit der Funktion f₁ (x) und eine Gerade mit der Funktion f₂ (x) schneiden sich in den Punkten P₁ und P₂ , wobei P₁ der höher liegende Punkt sein soll. Berechne:

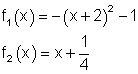
a) Die Schnittpunkte P₁ und P₂.
b) Die Funktion f₃ (x) der Geraden, die die Gerade mit der Funktion f₂ (x) im Punkt P₁ rechtwinklig schneidet.
c) Die Achsenschnittpunkte der drei Funktionen.
d) Zeichne die Graphen.

3.

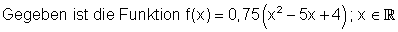
a)

b) Die Ursprungsgerade h(x) berührt f(x). Berechnen Sie die Koordinaten des Berührungspunktes, wenn gilt:

c) Eine auf h(x) senkrecht stehende Gerade i(x) schneidet f(x) in x = 3.
Bestimmen Sie die Funktionsgleichung von i(x).

4.

Eine Parabel mit der Funktion f₁ (x) und eine Gerade mit der Funktion f₂ (x) schneiden sich in den Punkten P₁ und P₂ , wobei P₁ der höher liegende Punkt sein soll.
Berechnen Sie:

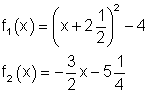
a) Die Schnittpunkte P₁ und P₂.
b) Die Funktion f₃ (x) der Geraden, die die Gerade mit der Funktion f₂ (x) im Punkt P₁ rechtwinklig schneidet.
c) Die Achsenschnittpunkte der drei Funktionen.
d) Zeichne die Graphen.

5.

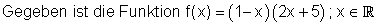
a) Bestimmen Sie die Achsenschnittpunkte von f(x)
b) Die Gerade g(x) verläuft parallel zur x- Achse durch den Punkt P( 1 | 3 ).
Bestimmen Sie die Schnittpunkte von f(x) und g(x).
c) Bestimmen Sie die Anzahl der Schnittpunkte von h(x) mit f(x) in Abhängigkeit von der Variablen b, wenn gilt:

Hier findest du die Lösungen.

hier die dazugehörige Theorie: Zusammenfassung Quadratische Funktionen.

Und hier eine Übersicht über weitere Beiträge zu quadratische Funktionen, darin auch Links zu weiteren Aufgaben.