In diesem Beitrag stelle ich eine Formelsammlung Quadratische Funktionen zur Verfügung. Wenn du mehr wissen willst, klick auf den Link zu dem jeweiligen Beitrag.
Funktionsgleichung:
Die Funktionsgleichungen haben die Form:
![]()
Solche Funktionen nennt man quadratische Funktion oder auch ganzrationale Funktionen 2. Grades. Die Graphen werden Parabeln genannt.
Scheitelpunkt-Scheitelpunktform

Darüber erfährst du mehr in dem Beitrag: Einführung in quadratische Funktionen.
Achsenschnittpunkte
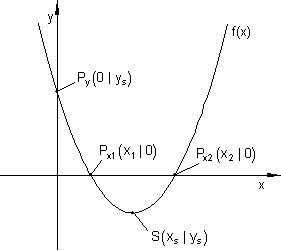
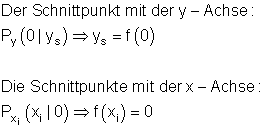
Wenn du mehr darüber lesen willst: Achsenschnittpunkte, p-q-Formel und Linearfaktoren.
Symmetriebetrachtungen
Die abgebildete Parabel ist symmetrisch zu der Achse, die parallel zur y-Achse durch den Scheitelpunkt verläuft.
Dies gilt für alle Parabeln.
Die Gleichung der Symmetrieachse durch den Scheitel S( xs | ys ) lautet: x = xs hier x = 3.
Auch die Nullstellen sind symmetrisch zur Symmetrieachse. Das bedeutet, bei bekannten Nullstellen kann der x-Wert des Scheitels berechnet werden.
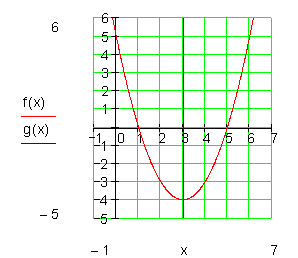
Scheitelpunktberechnung über die Nullstellen:
![]()
Das kannst du ebenfalls hier nachlesen: Achsenschnittpunkte, p-q-Formel und Linearfaktoren.
p-q-Formel, Diskriminante und Lösungsmenge

Das ist in diesem Beitrag vertieft: Achsenschnittpunkte, p-q-Formel und Linearfaktoren.
Der Satz von Vieta
![]()
Hier verweise ich ebenfalls auf: Achsenschnittpunkte, p-q-Formel und Linearfaktoren.
Nullstellen und Linearfaktoren

Das kannst du ebenfalls hier nachlesen: Achsenschnittpunkte, p-q-Formel und Linearfaktoren.
Der Satz vom Nullprodukt
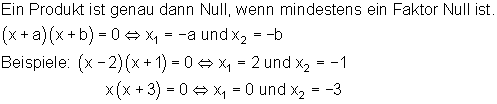
Schnittpunkte von Parabel und Gerade

Darüber erfährst du mehr in dem Beitrag: Schnittpunkt von Parabel und Gerade.
Schnittpunkte zweier Parabeln

Mehr zu diesem Thema findest du unter Schnittpunkt zweier Parabeln.
Hilfreiche Tools
Und zum Schluß eine Übersicht über meine interaktiven Javascripte:
Parabelplotter:
Gib Werte für die einzelnen Teile des Terms ein, wähle Zoom, Gitterabstand und Zeichenfläche. Nachdem du auf ‚Zeichnen‘ geklickt hast, kannst du die Parabale bewundern.
Parabelanalysator:
Gib die Koeffizienten ein. Klick danach auf ‚Zeichnen‘ und ‚Berechnen‘. Das Javascript analysiert und zeichnet dann die Parabel.
Parabel durch drei Punkte:
Wenn di die drei Punkte eingibst, berechnet und zeichnet das Programm die Parabel.
Gib die Koeffizienten beider Funktionsgleichungen ein. Danach berechnet das Javascript die Schnittpunkte und zeichnet die beiden Graphen.
Schnittpunkt von Parabel und Gerade:
Nachdem du die Koeffizienten beider Funktionsgleichungen eingegeben hast, berechnet das Javascript die Schnittpunkte und zeichnet beide Graphen.
Hier findest du eine Übersicht über weitere Beiträge zu Quadratischen Funktionen, darin auch Links zu weiteren Aufgaben.
Dazu kannst auch den Wikipedia-Artikel zu quadratischen Funktionen lesen.


