Nachdem wir uns intensiv mit quadratischen Funktionen beschäftigt haben, gebe ich hier eine Übersicht, wie man ökonomische Probleme mittels linearer und quadratischer Funktionen lösen kann. Zuerst stelle die Formeln für die Kostenrechnung vor. Danach zeige ich, wie man mithilfe der Erlösfunktions-Formel das Erlösmaximum und die Erlösschwelle errechnet. Anschließend zeige ich, wie man mithilfe der Gewinnfunktions-Formel das Gewinnmaximum errechnet. Zuletzt stelle ich die Kostenfunktion, die Erlösfunktion und die Gewinnfunktion in einem Graphen anschaulich zusammen.
Formeln Kostenrechnung:
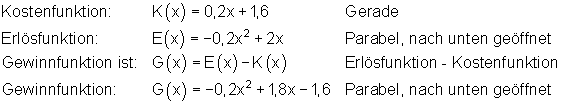
Definitionen ökonomischer Funktionen:
In der Kostenrechnung werden Fachbegriffe verwendet. Diese erkläre die ich hier kurz anhand des Beispiels und gebe die entsprechenden Formeln an:
Formel Erlösfunktion:
Die erlösmaximale Ausbringungsmenge und das Erlösmaximum erhält man, indem man den Term der Erlösfunktion E(x) in die Scheitelpunktform umwandeltund daraus den Scheitelpunkt abliest.
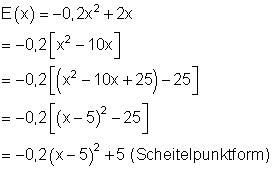
Dazu kannst du dir das 📽️Video Quadratische Ergänzung Scheitelpunkt bestimmen ansehen.
Bei einer Ausbringungsmenge von 5 ME ist der Erlös mit 5 GE maximal.
Erlösschwelle und -grenze:
Erlösschwelle und -grenze eines Betriebes sind die Stellen, an denen der Erlös Null ist.
Wir müssen also die Gleichung E(x) = 0 lösen:
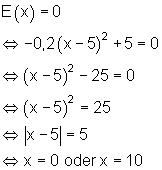
Hierzu kannst du dir das 📽️Video Quadratische Gleichungen lösen ausklammern ansehen.
Folglich liegt die Erlösschwelle bei 0 ME und Erlösgrenze bei 10 ME.
Gewinnschwelle und -grenze:
Gewinnschwelle und –grenze eines Betriebes sind die Stellen, an denen der Gewinn Null ist.
Hier müssen wir also die Gleichung G(x) = 0 lösen:
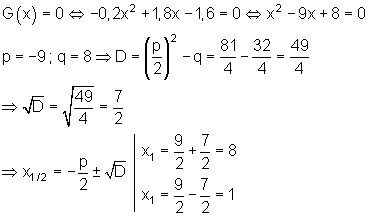
Hierzu kannst du dir das 📽️Video quadratische Gleichung mit der p-q-Formel lösen ansehen.
Folglich liegt die Gewinnschwelle bei 1 ME und Gewinngrenze bei 8 ME.
Formel Gewinnfunktion:
Die Gewinnmaximale Ausbringungsmenge und das Gewinnmaximum erhält man,indem man den Term der Gewinnfunktion G(x) in die Scheitelpunktform umwandeltund daraus den Scheitelpunkt abliest.
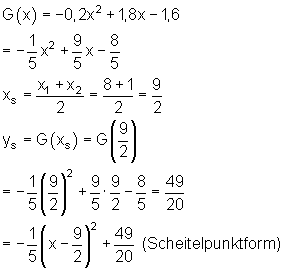
Dazu kannst du dir das 📽️Video Quadratische Ergänzung Scheitelpunkt bestimmen ansehen.
Bei einer Ausbringungsmenge von 4,5 ME ist der Gewinn also mit 2,45 GE maximal.
Graphen Kostenfunktion, Erlösfunktion und Gewinnfunktion:
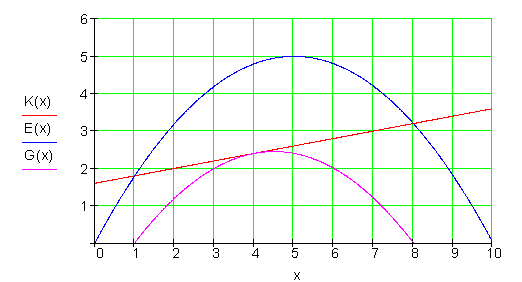
Zusammenfassung der Ergebnisse ökonomische Funktionen:
Bei einer Ausbringungsmenge von 5 ME ist der Erlös mit 5 GE maximal.
Die Erlösschwelle liegt bei 0 ME und die Erlösgrenze bei 10 ME.
Die Gewinnschwelle liegt bei 1 ME und die Gewinngrenze bei 8 ME.
Bei einer Ausbringungsmenge von 4,5 ME ist der Gewinn mit 2,45 GE maxima.
Hier findest du eine Übersicht über weitere Beiträge zu Quadratischen Funktionen, darin auch Links zu Aufgaben.


