Hier findest du die Lösungen der Aufgaben zu Parabel durch 3 Punkte.
1. Bestimme die Funktionsgleichung
a) Ausführliche Lösung
Allgemeine Form der Funktionsgleichung einer ganzrationalen Funktion 2. Grades (Parabel):
![]()
Werden die Koordinaten der 3 vorgegebenen Punkte in die allgemeine Funktionsgleichung eingesetzt, so erhält man ein Gleichungssystem bestehend aus 3 Gleichungen mit den 3 Variablen a2 ; a1 ; und a0.
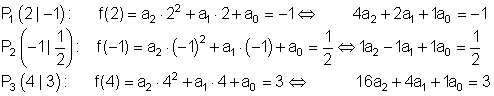
Lösung durch Additionsverfahren oder Gauß- Algorithmus:
Dazu kannst du dir das 📽️Video Funktionsgleichung Parabel durch drei Punkte ansehen.
Außerdem da 📽️Video Gauss-Algorithmus 3 Gleichungen mit 3 Variablen lösen.
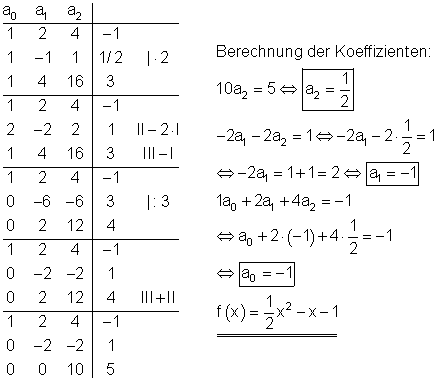
1. b) Ausführliche Lösung
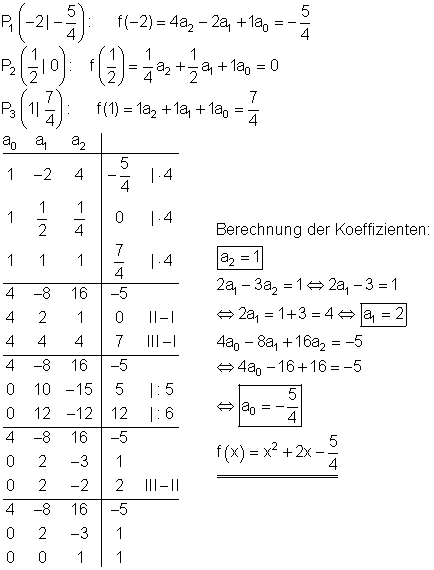
1. c) Ausführliche Lösung
Aus der Achsensymmetrie folgt: Der Scheitel liegt auf der y-Achse.
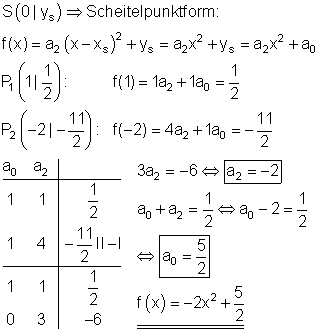
1. d) Ausführliche Lösung

1. e) Ausführliche Lösung
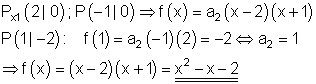
1. f) Ausführliche Lösung
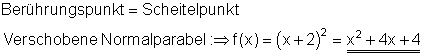
2. Drei sich schneidende Geraden bilden die Seiten eines Dreiecks
a) Ausführliche Lösungen
Folgende Geraden bilden ein Dreieck:
![]()
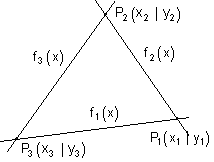
Definition der Schnittpunkte zur Berechnung der Eckpunkte des Dreiecks.
- P1 : f1 (x) geschnitten mit f2 (x)
- P2 : f2 (x) geschnitten mit f3 (x)
- P3 : f1 (x) geschnitten mit f3 (x)
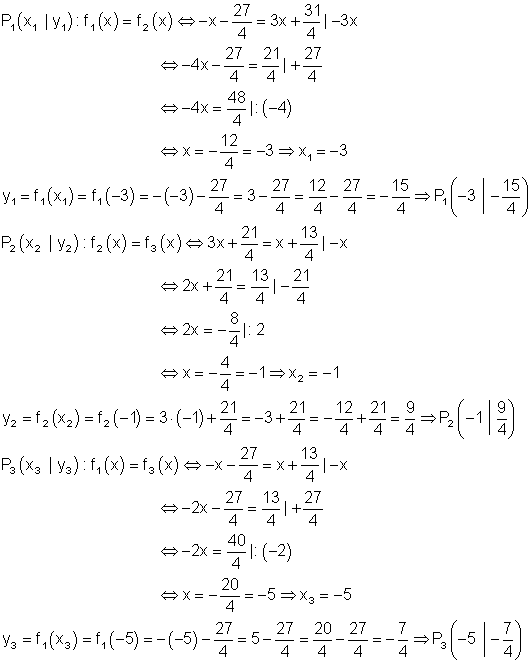
Berechnung der Funktionsgleichung der Parabel, deren Graph durch die Eckpunkte des Dreiecks verläuft.
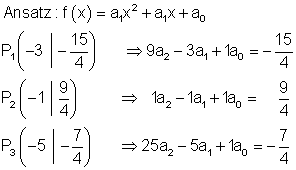
Lösung des Gleichungssystems durch den Gauß- Algorithmus.
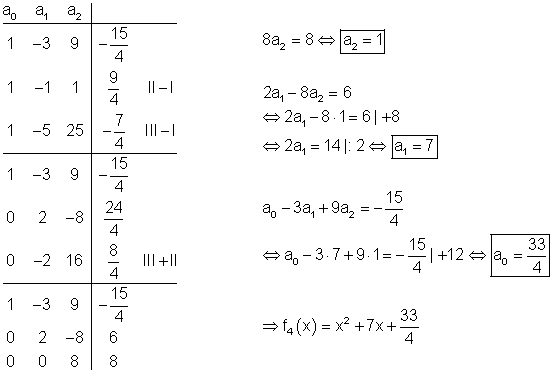
Um die Parabel zeichnen zu können, ist es sinnvoll die Achsenschnittpunkte und den Scheitelpunkt zu berechnen.
Berechnung der Achsenschnittpunkte.
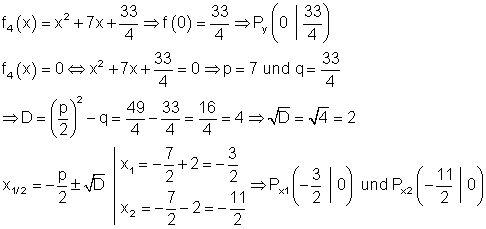
Scheitelpunktberechnung über die Nullstellen:
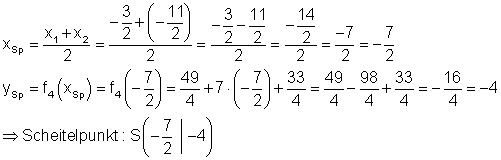
b) Die Graphen:
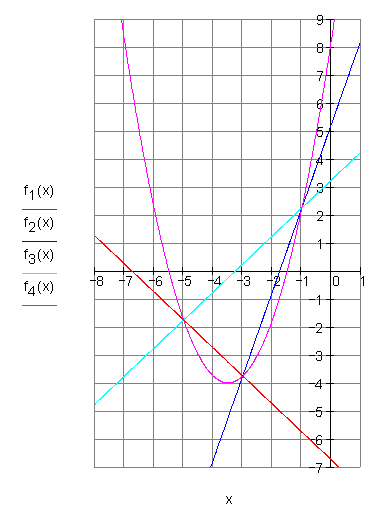
3. Berechne und zeichne
a) Berechnung der Funktionsgleichung:
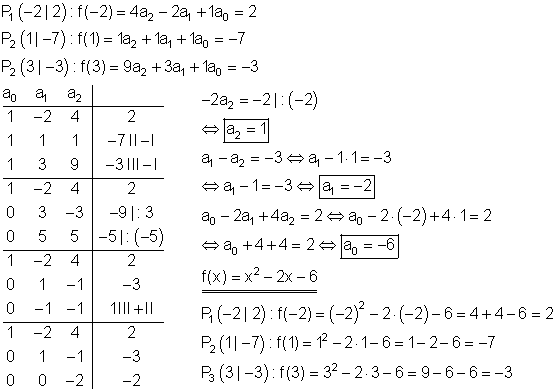
Berechnung der Achsenschnittpunkte:

Scheitelpunkt und Scheitelpunktform:
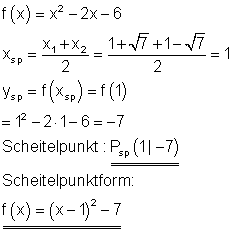
Der Graph:
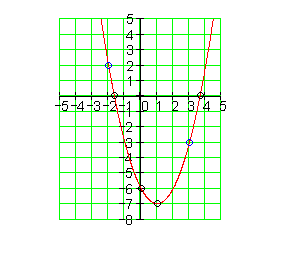
3. b) Ausführliche Lösung
Berechnung der Funktionsgleichung:
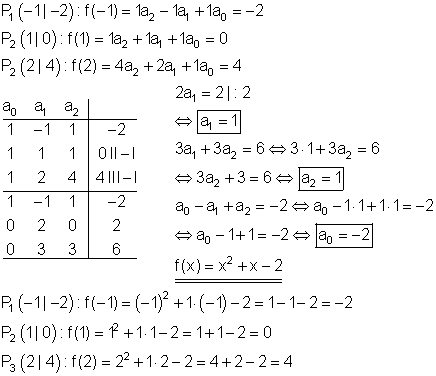
Berechnung der Achsenschnittpunkte:
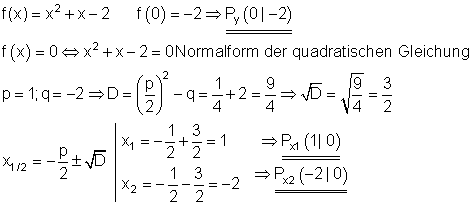
Scheitelpunkt und Scheitelpunktform:
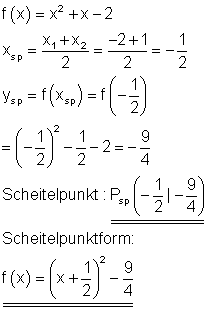
Der Graph:
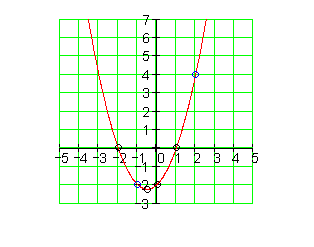
3. c) Ausführliche Lösung
Berechnung der Funktionsgleichung:
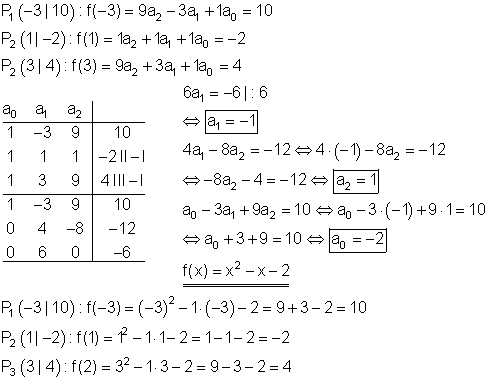
Berechnung der Achsenschnittpunkte:
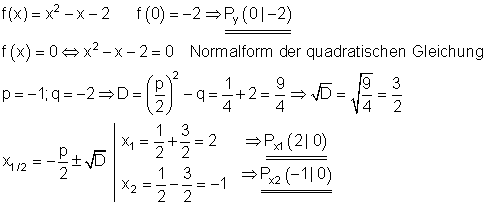
Scheitelpunkt und Scheitelpunktform:
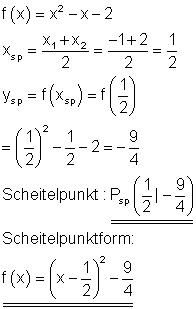
Der Graph:
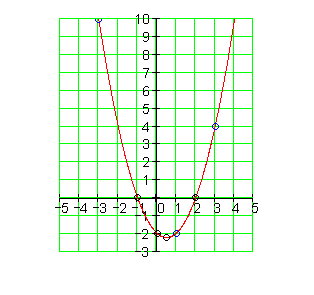
3. d) Ausführliche Lösung
Berechnung der Funktionsgleichung:
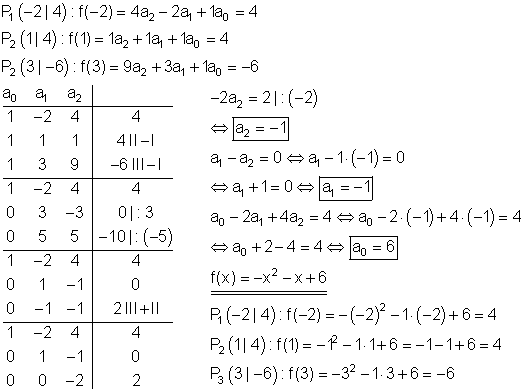
Berechnung der Achsenschnittpunkte:
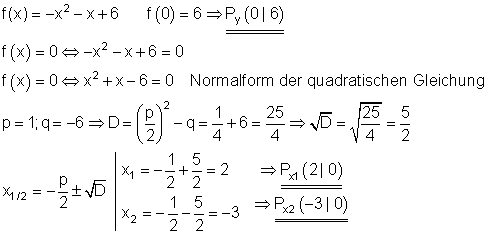
Scheitelpunkt und Scheitelpunktform:
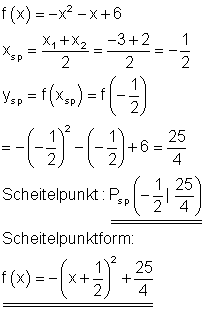
Der Graph:
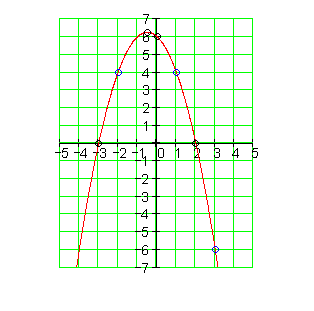
3. e) Ausführliche Lösung
Berechnung der Funktionsgleichung:
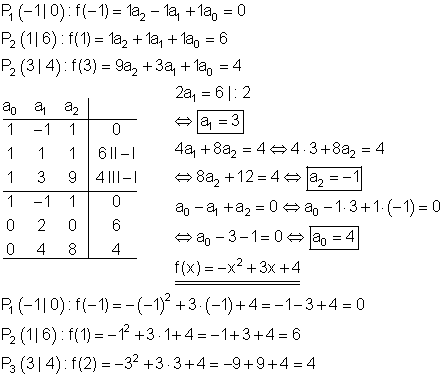
Berechnung der Achsenschnittpunkte:
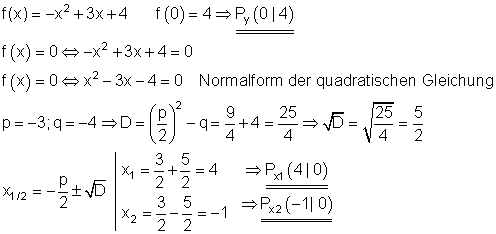
Scheitelpunkt und Scheitelpunktform:
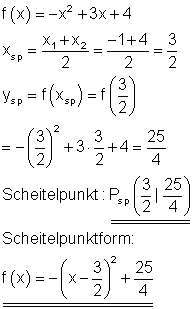
Der Graph:
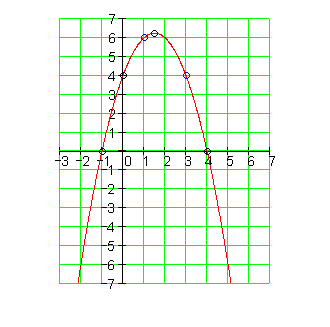
3. f) Ausführliche Lösung
Berechnung der Funktionsgleichung:
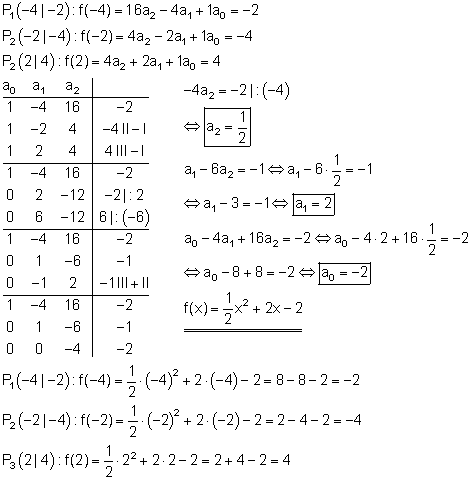
Berechnung der Achsenschnittpunkte:
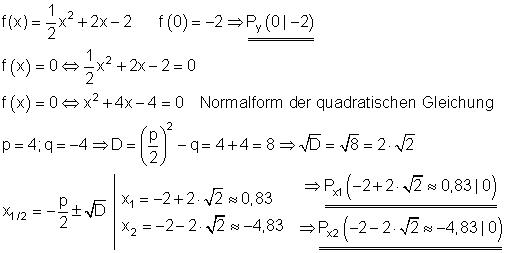
Scheitelpunkt und Scheitelpunktform:
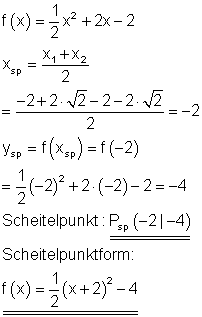
Der Graph:
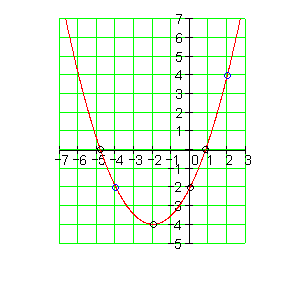
4. Berechne
a) Ausführliche Lösung
Berechnung der Funktionsgleichung:
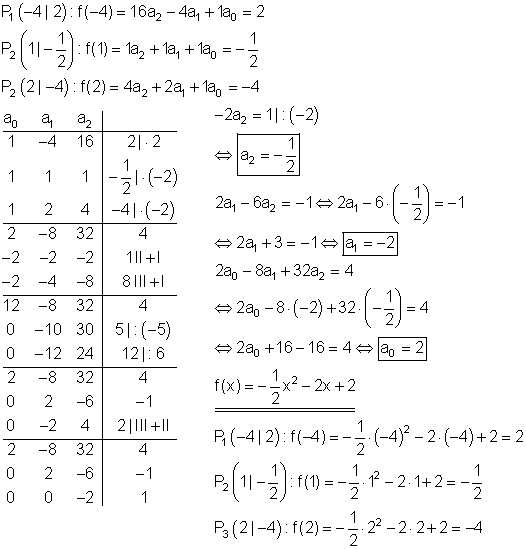
Berechnung der Achsenschnittpunkte:
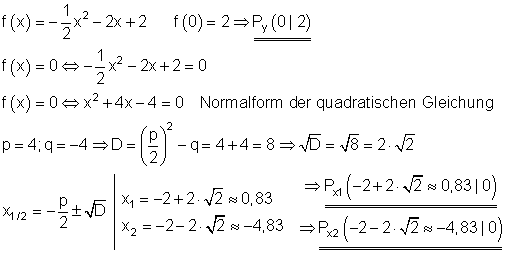
Scheitelpunkt und Scheitelpunktform:
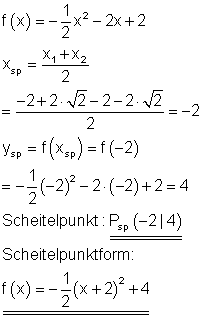
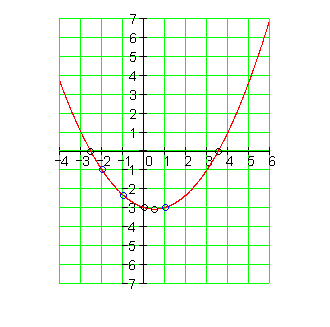
Der Graph:
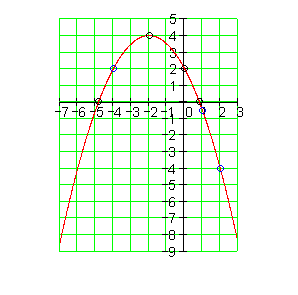
4. b) Ausführliche Lösung
Berechnung der Funktionsgleichung:
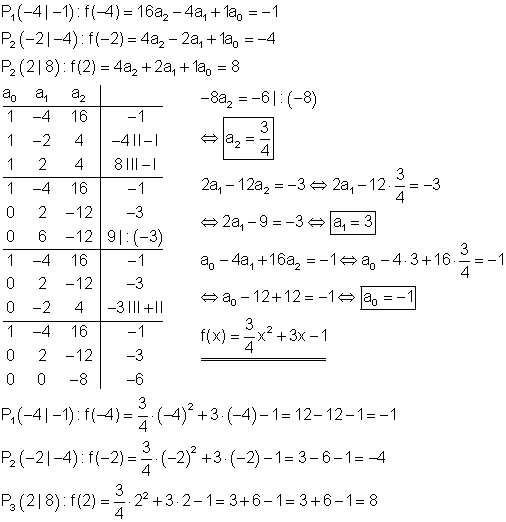
Berechnung der Achsenschnittpunkte:
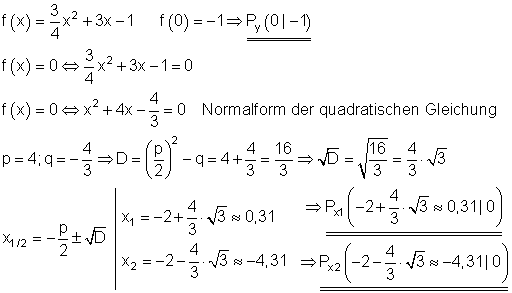
Scheitelpunkt und Scheitelpunktform:
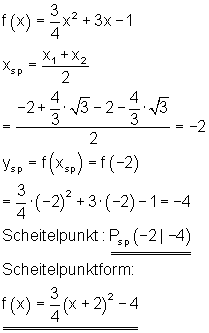
Der Graph:
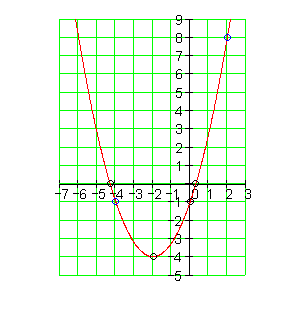
4. c) Ausführliche Lösung
Berechnung der Funktionsgleichung:
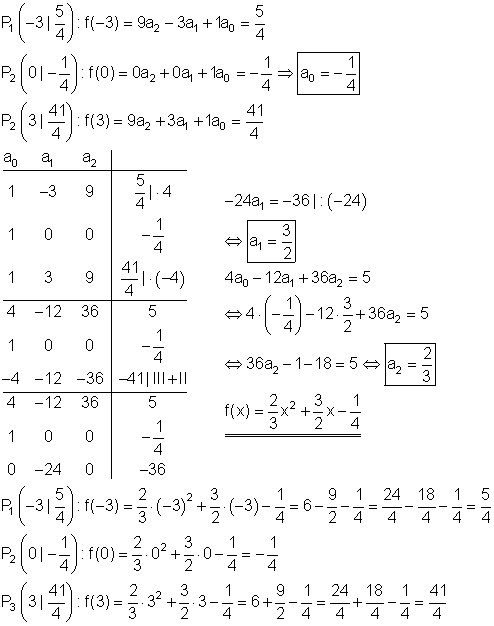
Berechnung der Achsenschnittpunkte:

Scheitelpunkt und Scheitelpunktform:
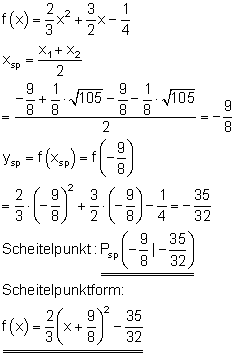
Der Graph:
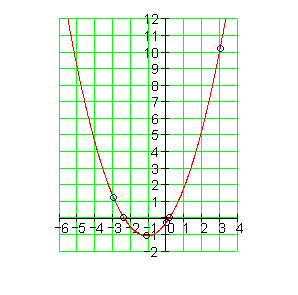
4. d) Ausführliche Lösung
Berechnung der Funktionsgleichung:
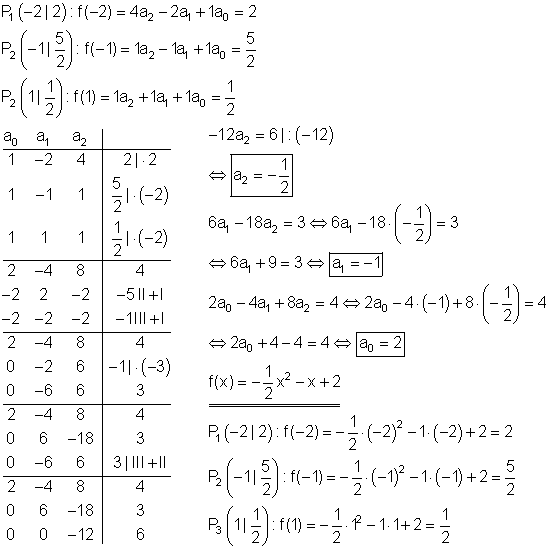
Berechnung der Achsenschnittpunkte:
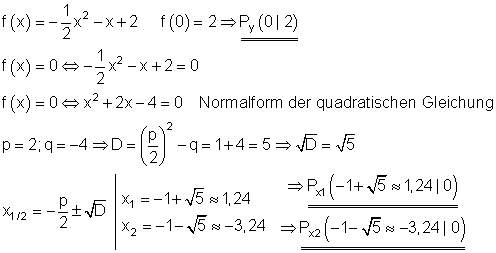
Scheitelpunkt und Scheitelpunktform:
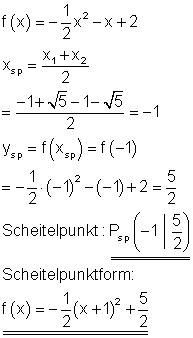
Der Graph:
4. e) Ausführliche Lösung
Berechnung der Funktionsgleichung:
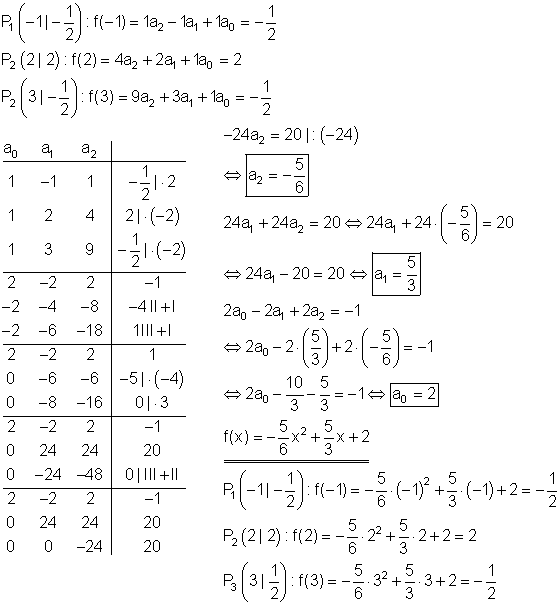
Berechnung der Achsenschnittpunkte:
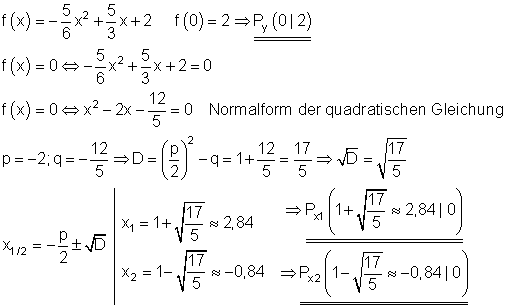
Scheitelpunkt und Scheitelpunktform:
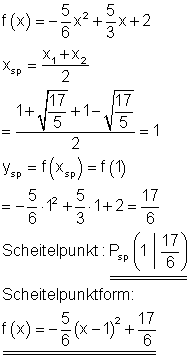
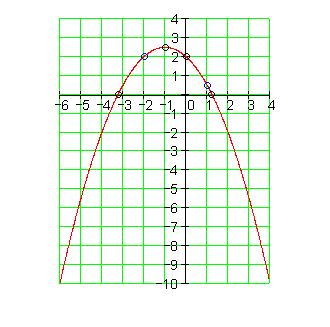
Der Graph:
4. f) Ausführliche Lösung
Berechnung der Funktionsgleichung:
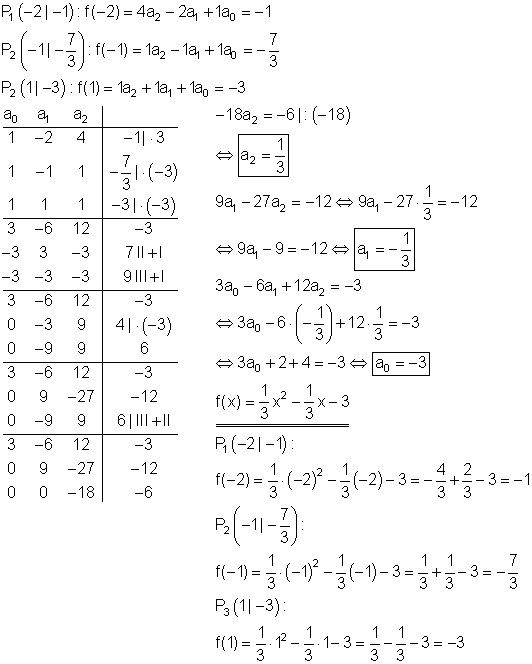
Berechnung der Achsenschnittpunkte:
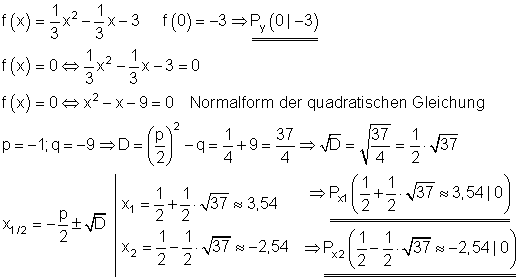
Scheitelpunkt und Scheitelpunktform:
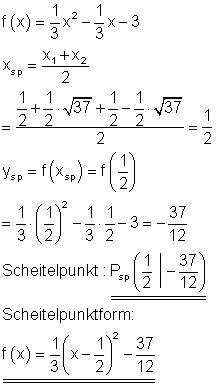
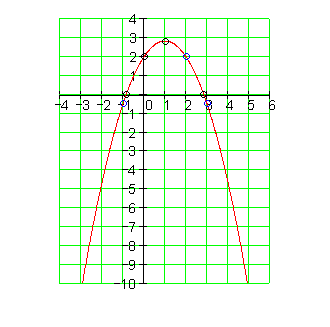
Der Graph:
5. Berechne
a) Ausführliche Lösung
Berechnung der Funktionsgleichung:
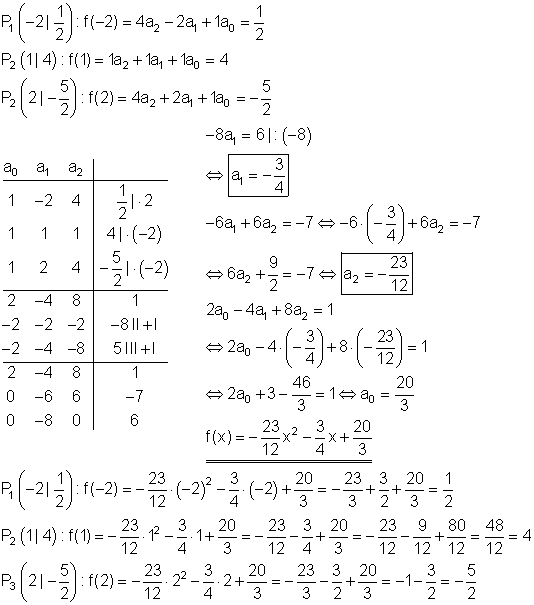
Berechnung der Achsenschnittpunkte:
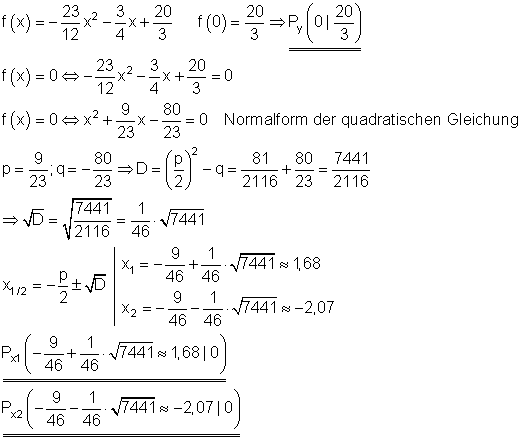
Scheitelpunkt und Scheitelpunktform:
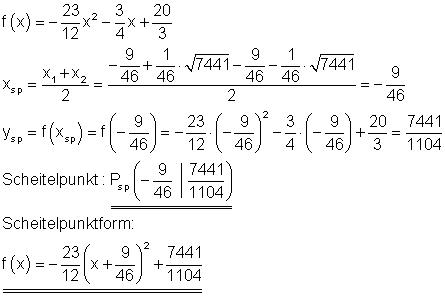
Der Graph:
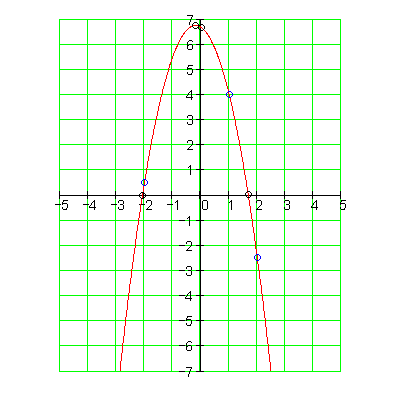
5. b) Ausführliche Lösung
Berechnung der Funktionsgleichung:
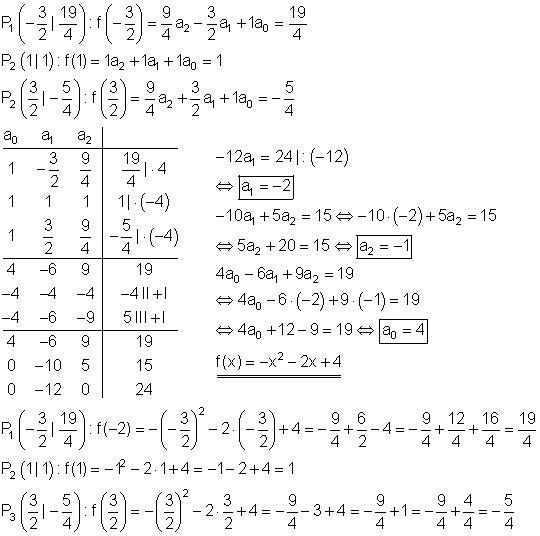
Berechnung der Achsenschnittpunkte:
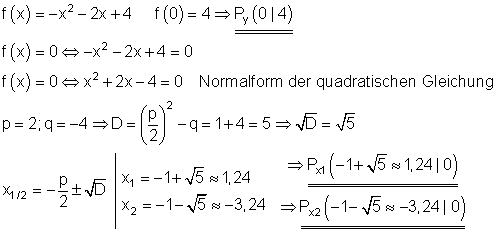
Scheitelpunkt und Scheitelpunktform:
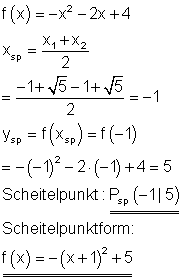
Der Graph:
5. c) Ausführliche Lösung
Berechnung der Funktionsgleichung:
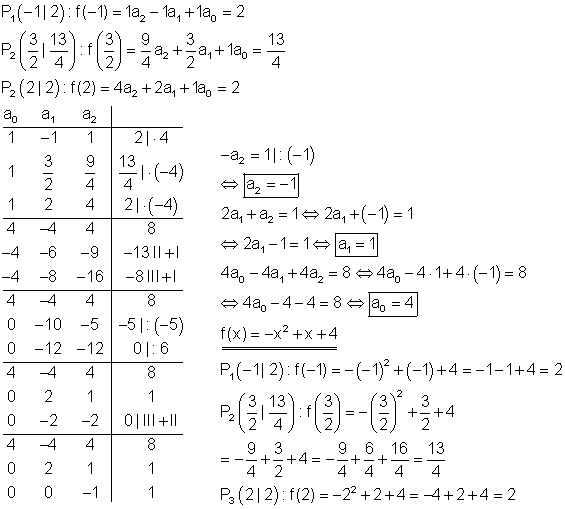
Berechnung der Achsenschnittpunkte:
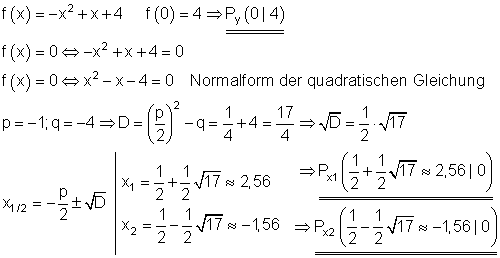
Scheitelpunkt und Scheitelpunktform:
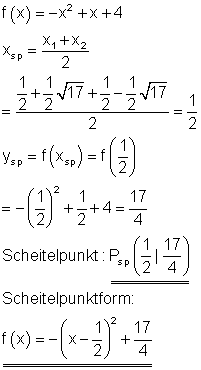
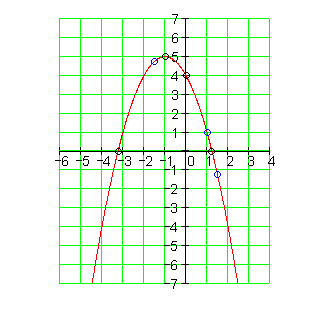
Der Graph:
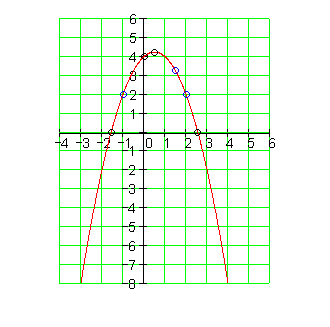
5d.Ausführliche Lösung
Berechnung der Funktionsgleichung:
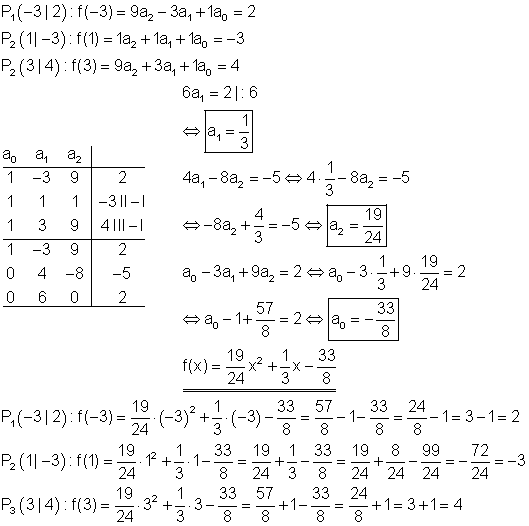
Berechnung der Achsenschnittpunkte:
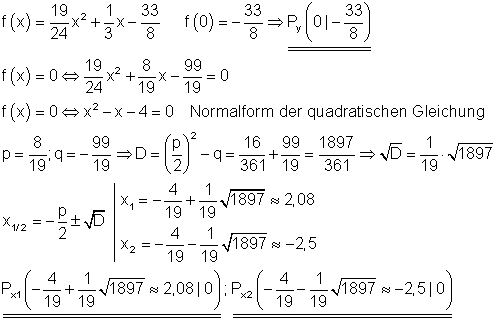
Scheitelpunkt und Scheitelpunktform:
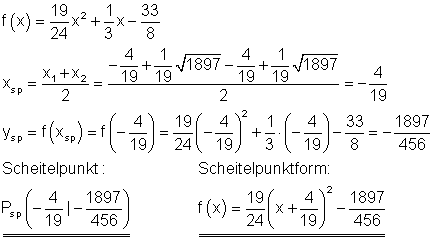
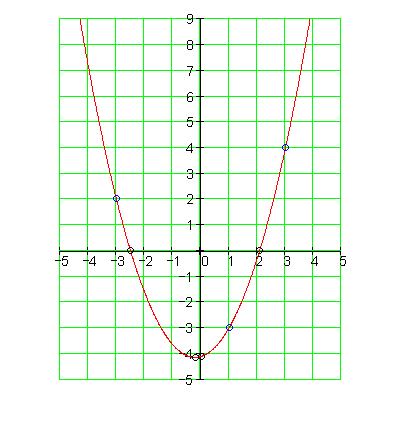
Der Graph:
5. e) Ausführliche Lösung
Berechnung der Funktionsgleichung:
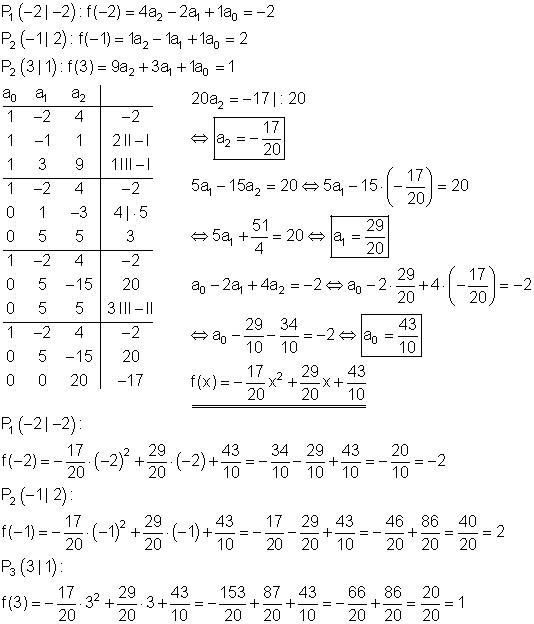
Berechnung der Achsenschnittpunkte:
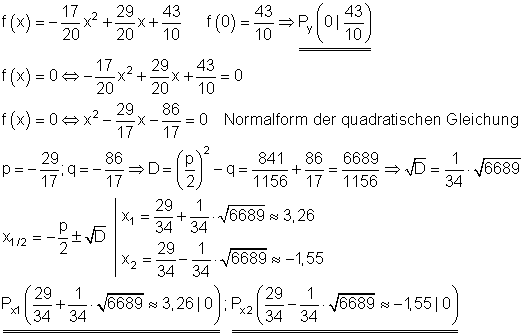
Scheitelpunkt und Scheitelpunktform:
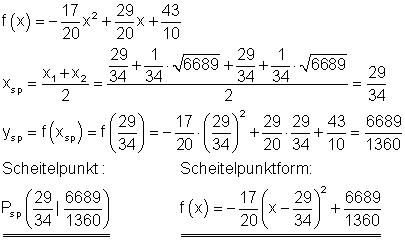
Der Graph:

5. f) Ausführliche Lösung
Berechnung der Funktionsgleichung:
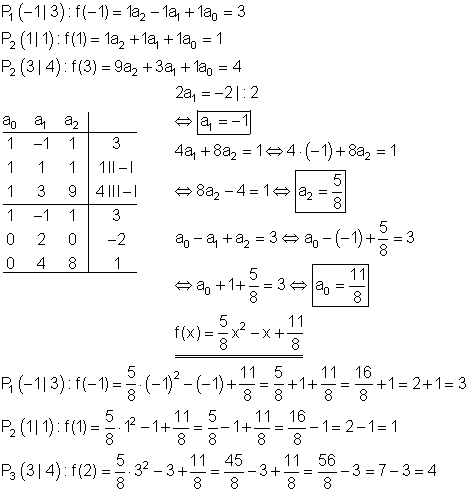
Berechnung der Achsenschnittpunkte:
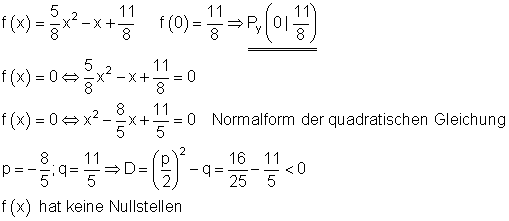
Scheitelpunkt und Scheitelpunktform:
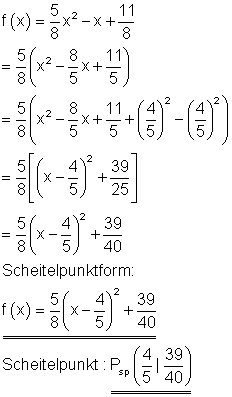
Der Graph:
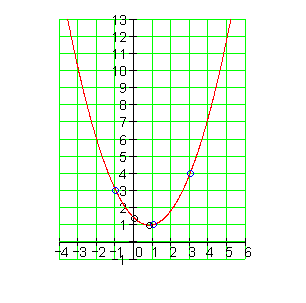
Dazu findest du hier die Aufgaben.
Hier die dazugehörige Theorie: Zusammenfassung Quadratische Funktionen.
Außerdem hier eine Übersicht über weitere Beiträge zu quadratische Funktionen, darin auch Links zu weiteren Aufgaben.

