Zuerst definiere ich den Begriff der Stetigkeit bei Funktionen und veranschauliche sie anhand einiger Beispiele. Danach stelle ich Beispiele für differenzierbarer Funktionen vor. Zuletzt erkläre ich die mathematische Definition der Differenzierbarkeit und die Mathematische Definition der Differenzierbarkeit.
- Stetigkeit Definition
- Differenzierbarkeit
- Beispiel stetig und differenzierbar
- Beispiele für stetig, aber nicht differenzierbar
- Mathematische Definitionen
- Links zu Aufgaben
Stetigkeit Definition
Eine Funktion f(x) heißt dann in einem Intervall [ a ; b ] stetig, wenn man den dazugehörigen Graphen von einem Intervallpunkt bis zum anderen zeichnen kann, ohne den Stift dabei absetzen zu müssen.
oder
Wenn sich die Punkte des Graphen der Funktion f(x) innerhalb eines Intervalls[ a ; b ] nahtlos aneinanderfügen, ohne dass sich irgendwelche Sprünge ergeben, dann ist die Funktion f(x) im Intervall [ a ; b ] stetig.
Beispiel für eine nicht stetige Funktion:

Beispiele stetiger Funktionen:
Jede ganzrationale Funktion ist auf ihrem Definitionsbereich stetig.
Jede gebrochen rationale Funktion ist in ihrem Definitionsbereich stetig.
Also nur dort unstetig, wo der Nenner Nullstellen hat, denn dort ist sie nicht definiert.
Für die klassische Betrachtung der Naturwissenschaften gilt: Die Natur macht keine Sprünge.
Danach verlaufen zahlreiche Naturvorgänge stetig:
Das Wachstum von Pflanzen und anderen Lebewesen mit der Zeit.
Die Druckerhöhung in einem Dampfkochtopf mit der Temperatur.
Es gibt aber auch unstetige (sprunghafte) Änderungen wie Gebühren bei Postsendungen oder Rabattstaffelungen.
Mathematische Definition der Stetigkeit:

Differenzierbarkeit
Beispiele differenzierbarer Funktionen
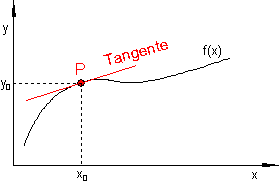
Die erste Ableitung einer Funktion an der Stelle x0 gibt die Steigung der Tangente an, die den Funktionsgraphen im Punkt P0 ( x0 | y0 ) berührt und ist damit zugleich die Steigung des Funktionsgraphen im Punkt P0 ( x0 | y0 ).
Man sagt auch Steigung der Funktion.
Demzufolge ist eine Funktion an der Stelle x0 nur dann differenzierbar, wenn eine eindeutige Tangente existiert.
Eine Bedingung für die Differenzierbarkeit einer Funktion an der Stelle x0 ist:
Die Funktion muss an der Stelle x0 stetig sein.
Diese Forderung ist notwendig aber nicht ausreichend, wie folgendes Beispiel zeigt.
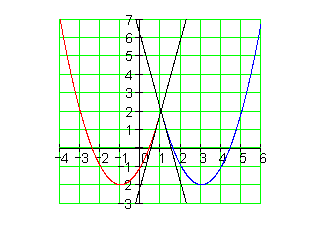
Beispiel stetig und differenzierbar:
Die Funktion f(x) ist für x = 1 stetig, es gibt dort keinen Sprung.
Wir haben aber im Punkt P( 1 | 2 ) zwei verschiedene Tangenten.
Das bedeutet, für x = 1 gibt es auch zwei Tangentensteigungen, also zwei Ableitungswerte.
Das bedeutet, die Ableitungsfunktion ist an der Stelle x = 1 nicht eindeutig.
Das hat zur Folge, dass f(x) an der Stelle x = 1 nicht differenzierbar ist.
Mit anderen Worten:
Eine Funktion f(x) ist an der Stelle x0 differenzierbar, wenn die Ableitung an dieser Stelle eindeutig ist, also genau eine Tangente existiert.
Anders ausgedrückt, an Stellen, an denen der Graph einer Funktion Spitzen oder Knicke besitzt, ist die Funktion nicht differenzierbar.
Umgekehrt bedeutet das für die Stetigkeit:
Ist eine Funktion an der Stelle x0 differenzierbar, dann ist sie dort auch stetig.
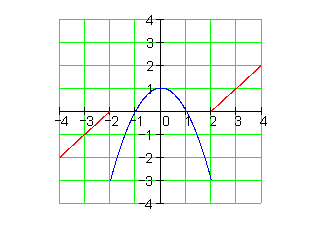
Weitere Beispiele für stetig, aber nicht differenzierbar:
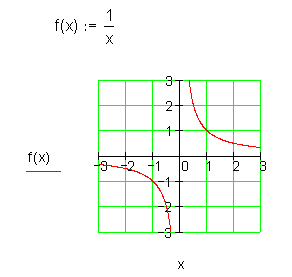
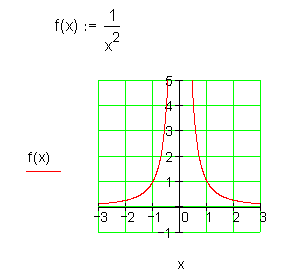
Beide Funktionen sind an der Stelle x0 = 0 nicht differenzierbar, weil sie dort nicht definiert sind.
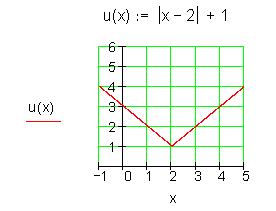
u(x) ist an der Stelle x0 = 2 zwar stetig, aber nicht differenzierbar (Spitze).

An der Stelle x0 = 1 ist die Funktion zwar stetig aber nicht differenzierbar (Knick).
Mathematische Definition der Differenzierbarkeit

Mathematische Definition der Integrierbarkeit
Eine Funktion ist integrierbar, wenn sie zumindest stückweise stetig ist.
Beispiele integrierbarer Funktionen
Gesucht ist die schraffierte Fläche.
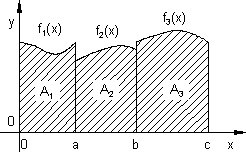
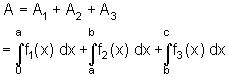
Gesucht ist die Dreiecksfläche.
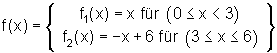
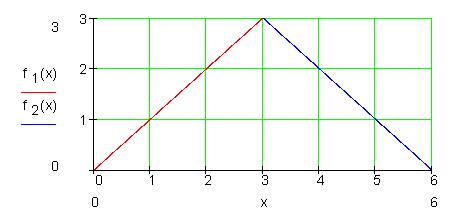
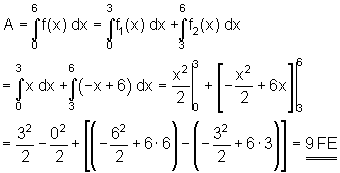
Obwohl die Funktion an der Stelle P ( 3 | 3 ) nicht differenzierbar ist, kann die Fläche über zwei Teilintegrale gefunden werden.
und Aufgaben Differential- und Integralrechnung, vermischte Aufgaben I.