In diesem Beitrag erkläre ich anhand anschaulicher Beispiele die Lösung unbestimmter Integrale durch Substitution. Zuletzt stelle ich Aufgaben dazu zur Verfügung.
Wenn du auf einen der Links hier klickst, gelangst du sofort zu dem entsprechenden Kapitel:
- Beispiel Anwendung der Grundintegrale nicht möglich
- Beispiele Integration mit Substitution
- Lösung bestimmter Integrale durch Substitution mit Beispielen
- Trainingsaufgaben: Integration durch Substitution:
Bisher haben wir nur Integrationsaufgaben gelöst, die sich auf Ableitungen von Elementarfunktionen zurückführen ließen, siehe auch Integration der e-Funktion. Die sich daraus ergebenden Grundintegrale bildeten die Basis aller weiteren Lösungsansätze. Die direkte Anwendung der Grundintegrale ist nicht immer möglich. Schauen wir und dazu folgendes Beispiel an.
1. Beispiel Anwendung der Grundintegrale nicht möglich:
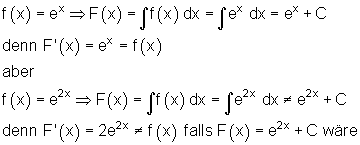
In solchen Fällen hilft jedoch die Methode der Substitution.
Beispiel Integration mit Substitution:
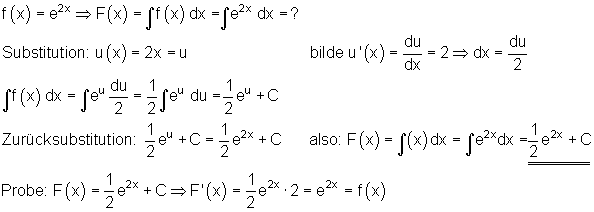
2. Beispiel Substitution unbestimmter Integrale:
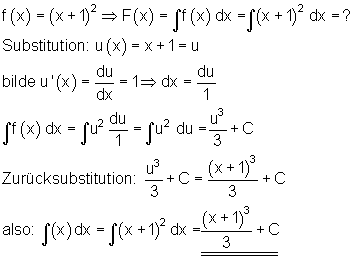
3. Beispiel:
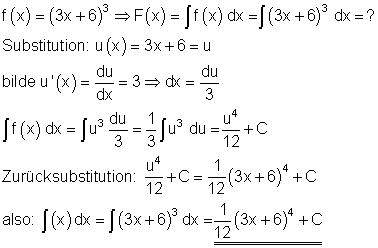
4. Beispiel:
Lösung bestimmter Integrale durch Substitution
Auch bestimmte Integrale lassen sich durch die Methode der Substitution lösen.
5. Beispiel Substitution bestimmter Integral:
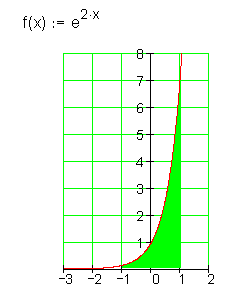
6. Beispiel:
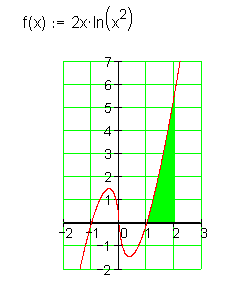
7. Beispiel:
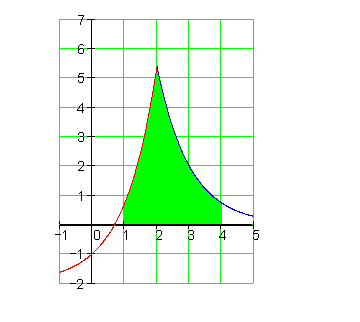
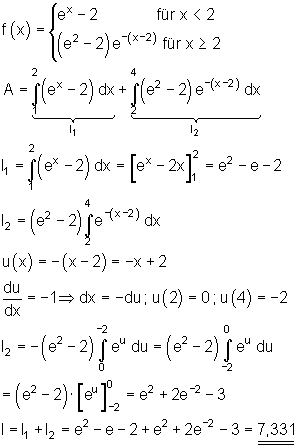
Aufgaben: Integration durch Substitution:
Löse, bzw. berechne folgende Integrale.
1. \int \frac{3}{4x + 1} dx
2. \int \limits_{0}^{2} \dfrac{4}{4 - x} dx
3. \int \dfrac{2} {(1 - x)^2} dx
4. \int \dfrac{6}{(2x - 1)^3} dx
5. \int \limits_{-2}^{2} \dfrac{10}{(x - 4)^5} dx
6. \int \limits_{-2}^{2} e^{1-x} dx
7. \int \limits_{0}^{4} e^{\frac{1}{2}x} dx
8. \int \limits_{1}^{2} e^{4-2x} dx
9. \int \limits_{1}^{2} \dfrac{4}{e^{2x-4}} dx
10. \int \limits_{0}^{2} (x - 1 - e^{-\frac{1}{2}x}) dx
Hier findest du die Lösungen.
Und hier die Theorie: Differentations und Integrationsregeln.
Hier findest du eine Übersicht über weitere Beiträge zur Fortgeschrittenen Differential- und Integralrechnung, darin auch Links zu weiteren Aufgaben.
