Hier findest du die ausführlichen Lösungen der Aufgaben zum Aufstellen der Funktionsgleichung aus gegebenen Bedingungen. Z. B. zu ganzrationale Funktionen durch 4 Punkte.
Teil I: Ganzrationale Funktionen durch 4 Punkte.
Finde jeweils die Funktionsgleichung und zeichne den Graphen! Berechne die Achsenschnittpunkte und fehlende Werte mit dem Hornerschema!
Zum Horner-Schema kannst du dir das Außerdem 📽️ Video Horner-Schema: Funktionswerte berechnen ansehen.
1.
P_1(1|4) ; P_2(2|2)
P_3(4|4) ; P_4(5|20)
Ausführliche Lösung
Als erstes stellen wir das Gleichungssystem auf:
f(x) = a_3x^3 + a_2x^2 + a_1x + a_0
P_1(1|4) \Rightarrow f(1) = 1a_3 + 1a_2 + 1a_1 + 1a_0 = 4 \\ P_2(2|2) \Rightarrow f(2) = 8a_3 + 4a_2 + 2a_1 + 1a_0 = 2 \\
P_3(4|4) \Rightarrow f(4) = 64a_3 + 16a_2 + 4a_1 + 1a_0 = 4 \\
P_4(5|20) \Rightarrow f(5) = 125a_3 + 25a_2 + 5a_1 + 1a_0 = 20 \\
Als nächstes tragen wir in eine Tabelle nach Gauß ein:
Dazu kannst du dir das 📽️Video Gauss-Algorithmus 3 Gleichungen mit 3 Variablen lösen ansehen.
| a0 | a1 | a2 | a3 | |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 4 |
| 1 | 2 | 4 | 8 | 2 II-I |
| 1 | 4 | 16 | 64 | 4 III-I |
| 1 | 5 | 25 | 125 | 20 IV-I |
| 1 | 1 | 1 | 1 | 4 |
| 0 | 1 | 3 | 7 | -2 |
| 0 | 3 | 11 | 63 | 0 III – 3 · II |
| 0 | 4 | 24 | 124 | 16 IV – 4 · II |
| 1 | 1 | 1 | 1 | 4 |
| 0 | 1 | 3 | 7 | -2 |
| 0 | 0 | 6 | 42 | 6 |
| 0 | 0 | 12 | 96 | 24 IV – 2 · III |
| 1 | 1 | 1 | 1 | 4 |
| 0 | 1 | 3 | 7 | -2 |
| 0 | 0 | 6 | 42 | 6 |
| 0 | 0 | 0 | 12 | 12 |
Daraus entwickeln wir jetzt die Funktionsgleichung:
\Rightarrow 12 a_3 = 12 \Leftrightarrow \underline{\underline{a_3 = 1}}
6a_2 + 42 = 6 | -42
\Leftrightarrow 6a_2 = -36 \Leftrightarrow \underline{\underline{a_2 = -6}}
a_1 + 3a_2 + 7a_3 = -2
\Leftrightarrow a_1 - 18 + 7 = -2 \\
\Leftrightarrow a_1 - 11 = -2 | +11 \Leftrightarrow \underline{\underline{ a_1 = 9}}
a_0 + a_1 + a_2 + a_3 = 4
\Leftrightarrow a_0 + 9 -6 + 1 = 4 \\
\Leftrightarrow a_0 + 4 = 4 | - 4 \Leftrightarrow \underline{\underline{ a_0 = 0}}
Die Funktionsgleichung lautet also:
\underline{\underline{ f(x) = x^3 - 6x^2 + 9x}}
Schließlich tragen wir die Werte in der Wertetabelle ein:
| x | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 | 5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f(x) | -6,12 | 0 | 3,13 | 4 | 3,37 | 2 | 0,62 | 0 | 0,87 | 4 | 10,12 | 20 |
Jetzt können wir den Graph zeichnen und folgendes berechnen:
Schnittpunkt mit der y-Achse:
f(0) = 0 \Rightarrow P_y(0|0)
Nullstellen:
f(x) = 0 \Leftrightarrow x^3 - 6x^2 + 9x = 0
Wenn wir dies faktorisieren:
x(x^2 - 6x + 9) = 0 \Rightarrow x_1 = 0
x^2 - 6x + 9 = 0
p = -6 ; q = 9 \Rightarrow D = 0 \\
x_{2/3} = -\frac{p}{2} = 3
P_{x1}(0|0)
P_{x2/3} (3|0)

2.
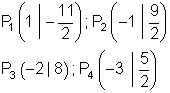
Ausführliche Lösung
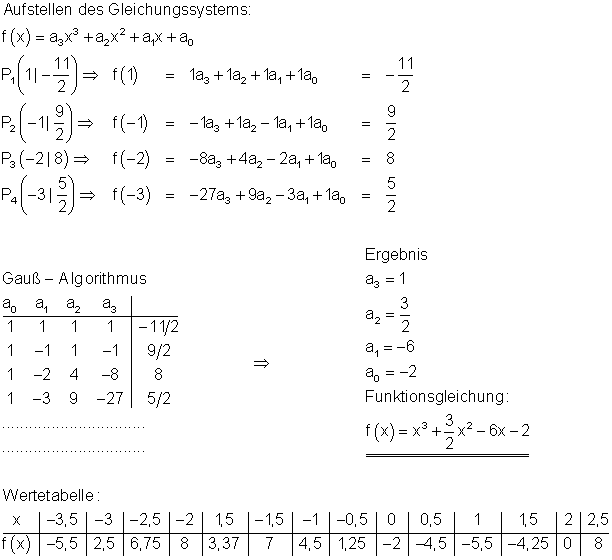
Ausführlicher Gauß- Algorithmus:
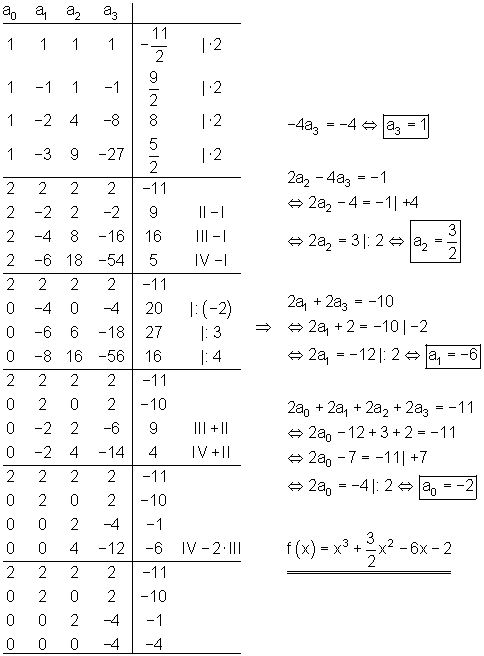
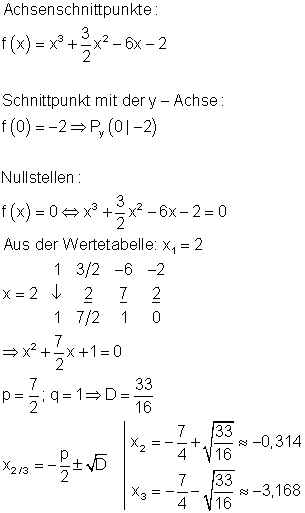
![]()
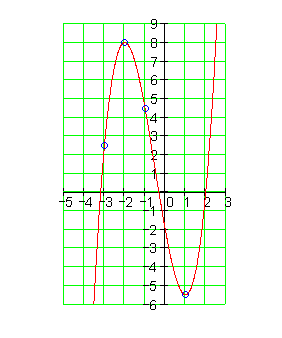
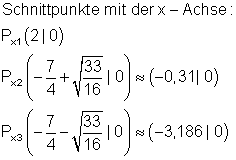
3.

Ausführliche Lösung
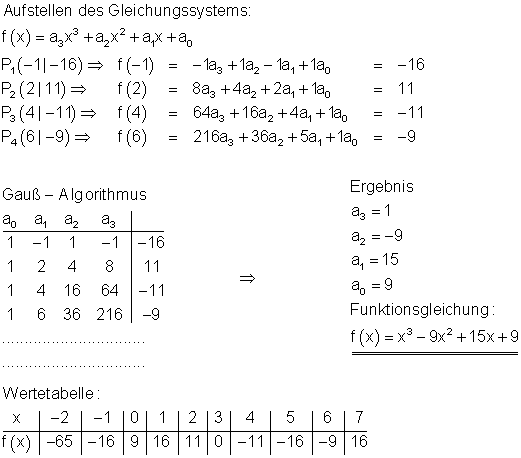
Ausführlicher Gauß- Algorithmus:
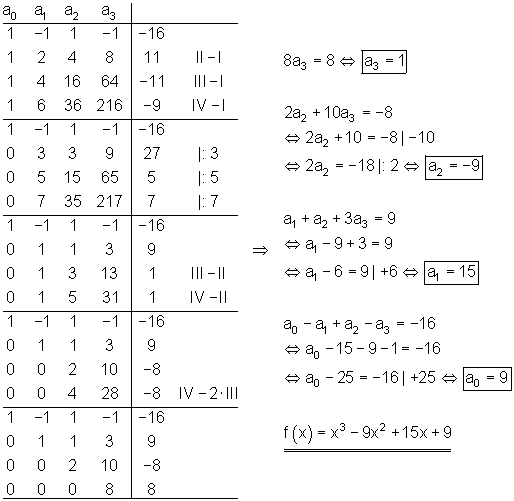
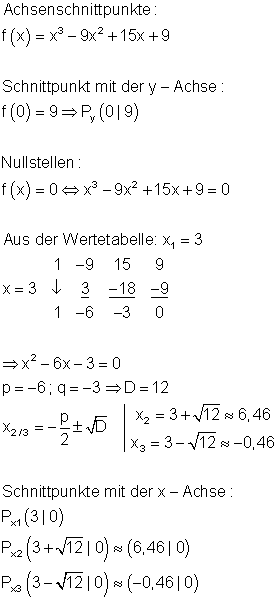
![]()
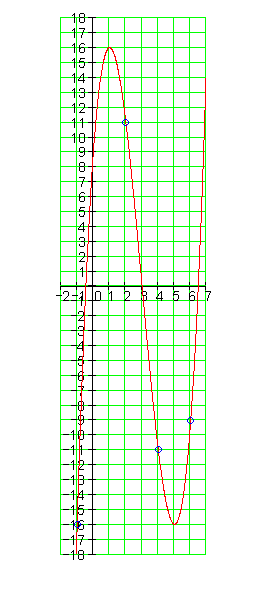
4.
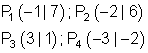
Ausführliche Lösung

Ausführlicher Gauß- Algorithmus:
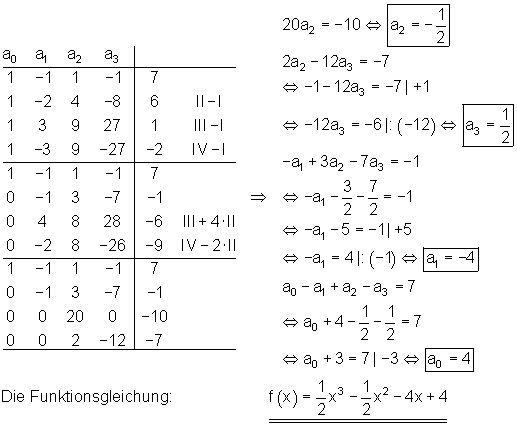
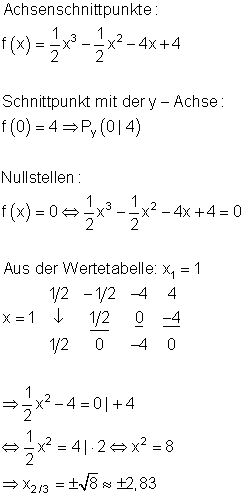
![]()
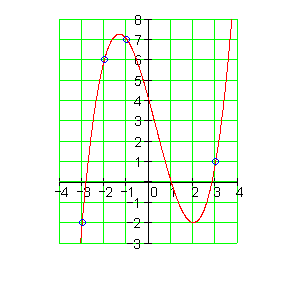

5.
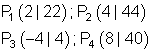
Ausführliche Lösung:

Ausführlicher Gauß- Algorithmus:
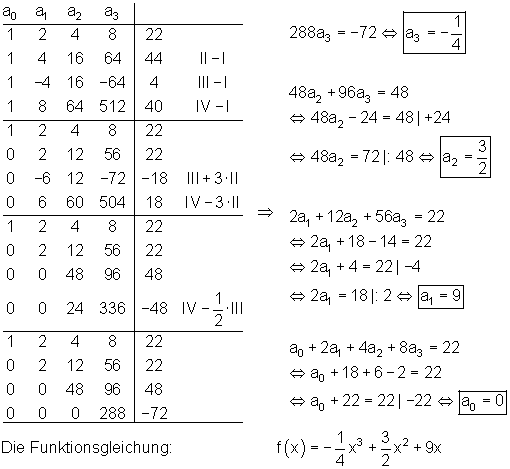
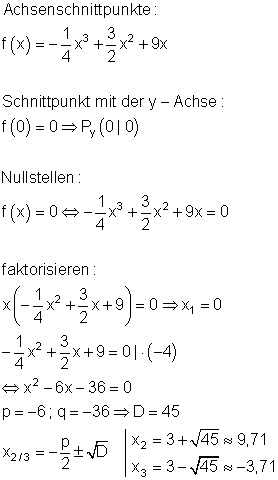
![]()
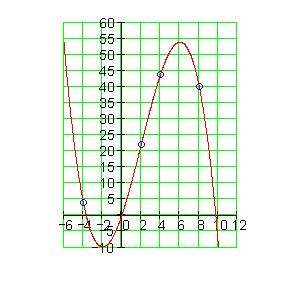

6.
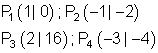
Ausführliche Lösung:

Ausführlicher Gauß- Algorithmus:
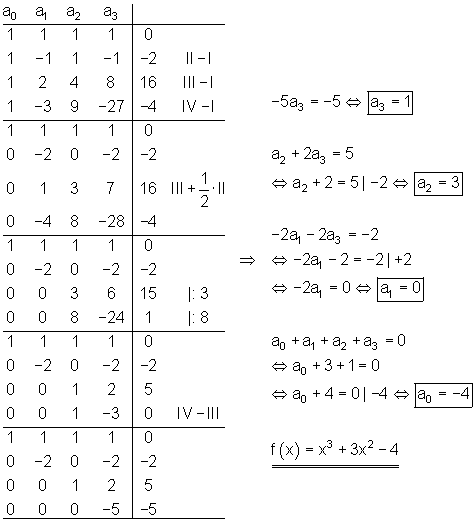

![]()

7.
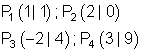
Ausführliche Lösung:

Ausführlicher Gauß- Algorithmus:
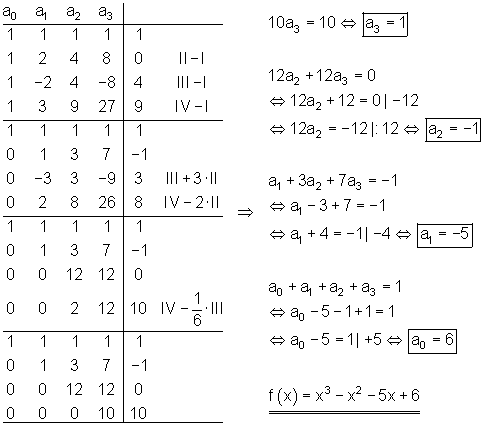

![]()
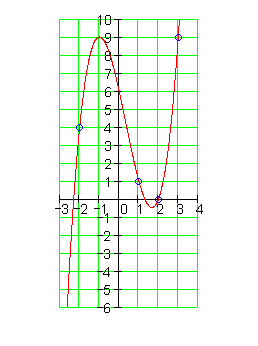
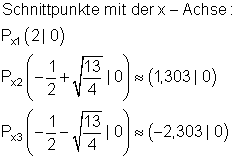
8.
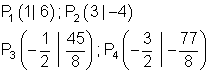
Ausführliche Lösung:
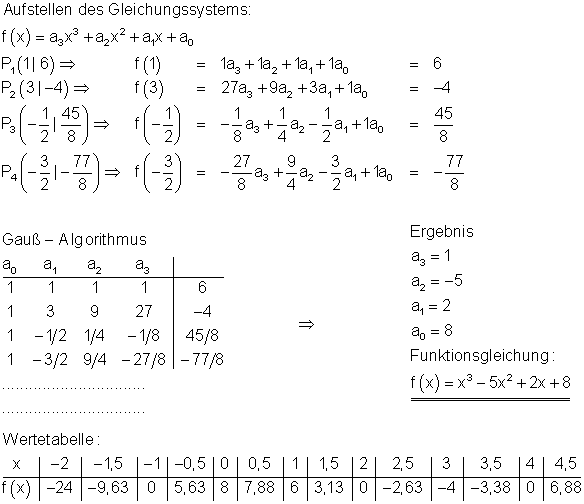
Ausführlicher Gauß- Algorithmus:
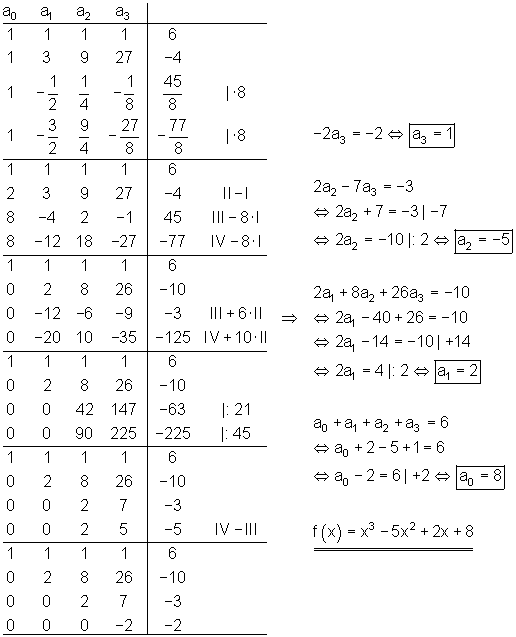

![]()
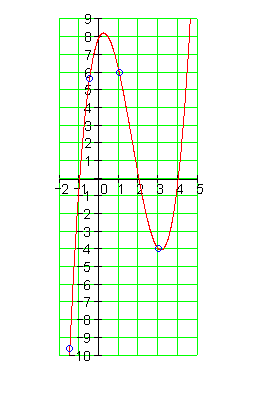
9.
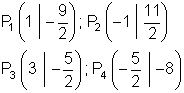
Ausführliche Lösung:
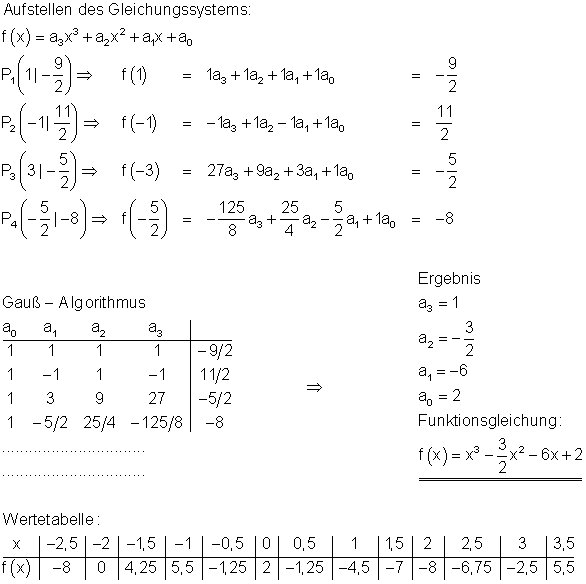
Ausführlicher Gauß- Algorithmus:
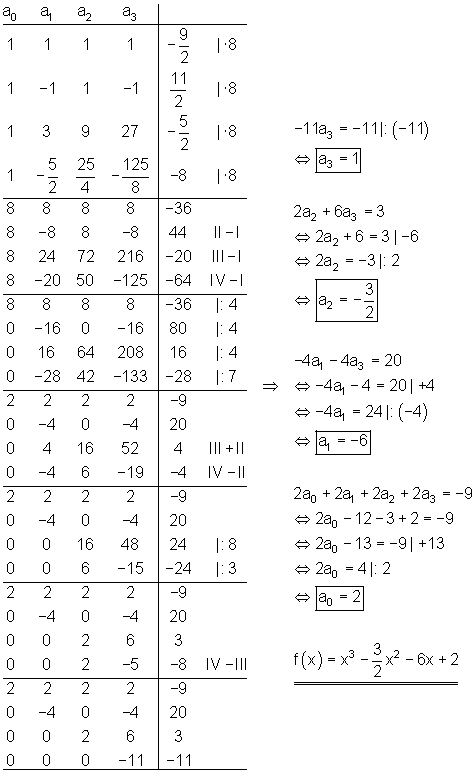

![]()
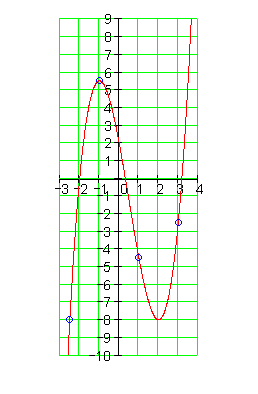
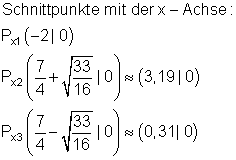
10.
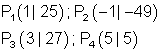
Ausführliche Lösung:

Ausführlicher Gauß-Algorithmus:


![]()
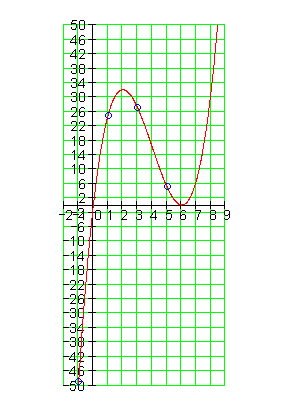
Teil II: Finden Sie jeweils die Funktionsgleichung und skizzieren Sie den Graphen.
11.
grad 3, punktsymmetrisch
P_1(2|3) P_2(-3|-2)
Ausführliche Lösung:
grad 3, punktsymmetrisch durch
P_1(2|3) P_2(-3|-2)
Wegen der Punktsymmetrie hat die Funktionsgleichung nur ungerade Exponenten.
Als erstes stellen wir den Ansatz auf:
f(x) = a_3x^3 + a_1x \\
P_1(2|3) \Rightarrow f(2) = 8a_3 + 2a_1 = 3 \\
P_2(-3|-2) \Rightarrow f(-3) = -27a_3 - 3a_1 = -2
| a1 | a3 | ||
| 2 | 8 | 3 | | · 3 |
| -3 | -27 | -2 | | · 2 |
| 6 | 24 | 9 | |
| -6 | -54 | -4 | II + I |
| 6 | 24 | 9 | |
| 0 | -30 | 5 |
Daraus entwickeln wir jetzt die Funktionsgleichung:
-30a_3 = 5 \Leftrightarrow a_3 = -\frac{1}{6}
6a_1 + 24a_3 = 9 \Leftrightarrow 6a_1 - 4 = 9 \Leftrightarrow a_1 = \frac{13}{6}
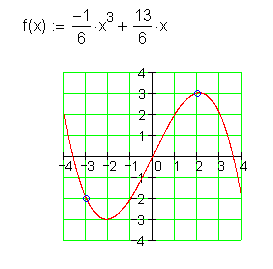
Ganzrationale Funktion 3. Grades ist symmetrisch zum Ursprung, bzw, punktsymmetrish mit drei Nullstellen. Bei Punktsymmetrie hat die Variable x nur ungerade Exponenten. Bei Achsensymmetrie sind sie gerade.
12.
![]()
Ausführliche Lösung:

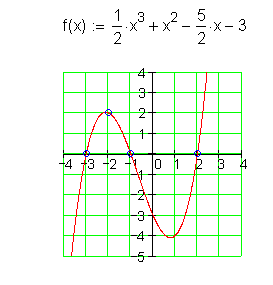
13.
Finden Sie die Funktionsgleichung und skizzieren Sie den Graphen.
![]()
Ausführliche Lösung:

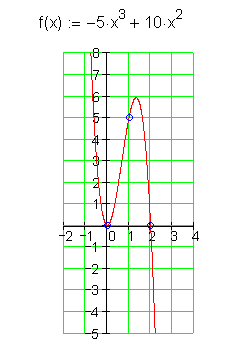
14.
Finden Sie die Funktionsgleichung und skizzieren Sie den Graphen.
![]()
Ausführliche Lösung:

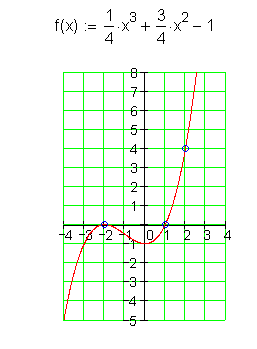
15.
Finden Sie die Funktionsgleichung und skizzieren Sie den Graphen.
![]()
Ausführliche Lösung:
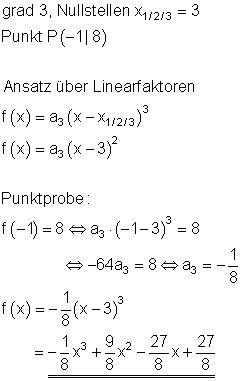
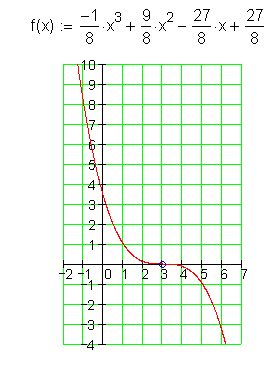
16.
Finden Sie die Funktionsgleichung und skizzieren Sie den Graphen.
![]()
Ausführliche Lösung:

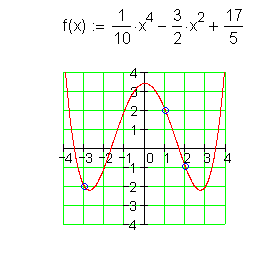
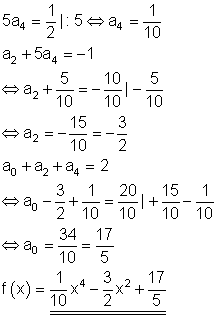
17.
Finden Sie die Funktionsgleichung und skizzieren Sie den Graphen.
![]()
Ausführliche Lösung:

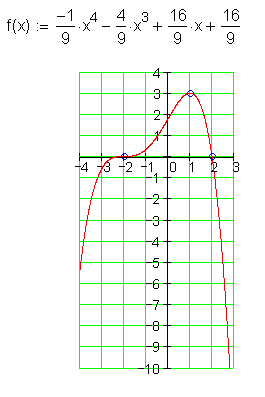
18.
Finden Sie die Funktionsgleichung und skizzieren Sie den Graphen.
![]()
Ausführliche Lösung:
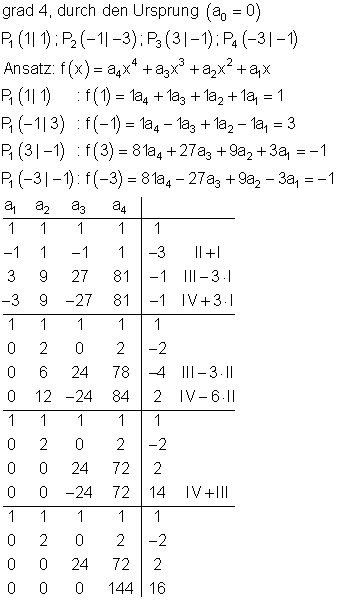
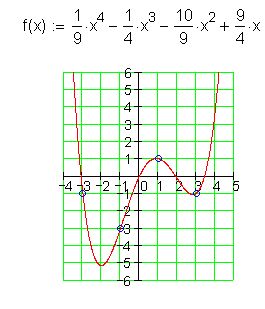
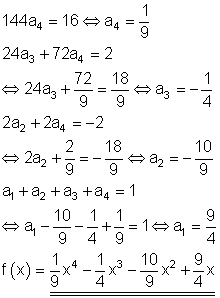
19.
Finden Sie die Funktionsgleichung und skizzieren Sie den Graphen.
![]()
Ausführliche Lösung:
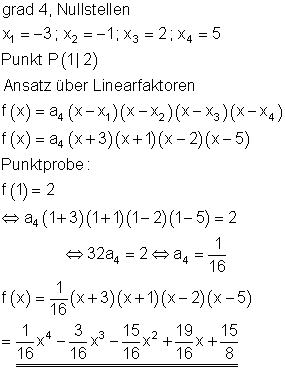
![]()
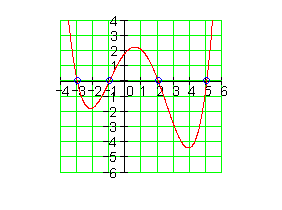
20.
Finden Sie die Funktionsgleichung und skizzieren Sie den Graphen.
![]()
Ausführliche Lösung:
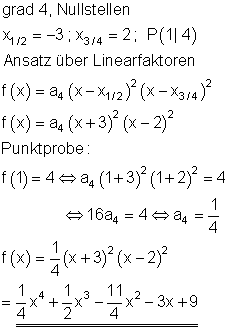
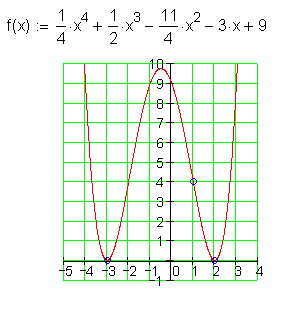
Dazu findest du hier die Aufgaben.
Und hier die Theorie dazu.
Hier findest du eine Übersicht über alle Beiträge zum Thema weitere ganzrationale Funktionen, darin auch Links zu weiteren Aufgaben.

