Bei diesen Aufgaben zu ganzrationalen Funktionen I handelt es sich um Textaufgaben und Anwendungsaufgaben aus Technik und Wirtschaft.
1. Herstellung einer Ware
Bei der Herstellung einer Ware entstehen Gesamtkosten in Abhängigkeit von der Stückzahl x
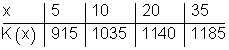
Bestimme einen Funktionsterm für die Gesamtkostenfunktion K(x).
Wie ist der Verkaufspreis je Stück zu wählen, damit für x = 15 kein Verlust entsteht? Stellen Sie den Sachverhalt graphisch dar.
Dazu kannst du dir das 📽️Video Gauss-Algorithmus 3 Gleichungen mit 3 Variablen lösen ansehen.
2. Flugkurve
Der Graph der Funktion f(x) ist näherungsweise die Flugkurve des Balls bei einem Freistoß in einem Fußballspiel.
![]()
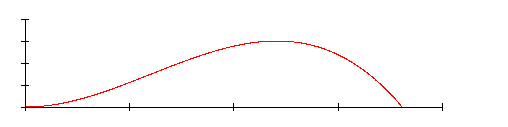
a) Welche maximale Höhe erreicht der Ball?
b) Überfliegt der Ball die Abwehrmauer (2 m hoch) in 9,15 m?
c) Wo kommt der Ball wieder auf den Boden?
d) Wie weit entfernt vom Tor wurde der Freistoß ausgeführt, wenn der Ball in 2 m Höhe die Torlinie überschreitet?
3. Giebel
Die Abbildung zeigt den Giebel eines Barock-Hauses (Maße in m).
a) Begründe, dass es sich bei der Randfunktion um eine ganzrationale Funktion 4. Grades handelt.
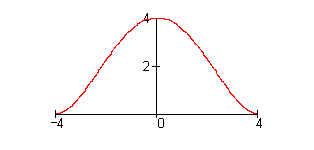
b) Bestimme den Funktionsterm.
c) Ein Fenster der Höhe 2,25 m soll in den Giebel eingepasst werden. Wie breit kann es höchstens sein?
4. Gebirgstal
Die symmetrische Querschnittsfläche eines Gebirgstales lässt sich durch eine ganzrationale Funktion 4. Grades beschreiben. Das Tal hat eine maximale Breite von 120 m und ist 360 m tief. Bei einer Breite von 60 m wird von der Talsohle aus eine Höhe von 157,5 m gemessen.
a) Bestimme den Funktionsterm.
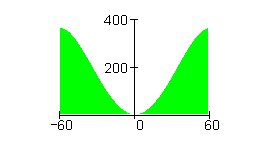
b) Ein 250 m hoher Staudamm soll errichtet werden. Wie breit ist die Dammkrone? Berechne auf eine Dezimalstelle genau.
Dazu findest du hier die ausführlichen Lösungen.
Und hier die dazugehörige Theorie: Aufstellen der Funktionsgleichung aus gegebenen Bedingungen
Hier eine Übersicht über weitere ganzrationale Funktionen, darin Links zu weiteren Aufgaben.

