Hier findest du Aufgaben aus dem Alltag zur Differentialrechnung I. Dabei müsst ihr die Steigung und Tangente berechnen.
1. Chemische Reaktionen können mit unterschiedlicher Geschwindigkeit ablaufen.
Bringt man z.B. Zink in Salzsäure, so entsteht Wasserstoff. Die folgende Tabelle gibt die Menge des Wasserstoffs in Abhängigkeit von der Zeit an:
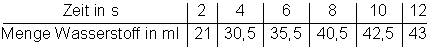
a) Erstelle hierzu ein Diagramm!
b) Was lässt sich über die Wasserstoffproduktion aussagen?
b) Berechne die Änderungsraten in den folgenden Intervallen:
[ 2 ; 4 ] ; [ 4 ; 8 ] ; [ 8 ; 12 ]
2. Berechne die Änderungsrate
von f(x) = \frac{1}{4}x^2 - x + 1 auf den Intervallen [1 ; 15] ; [-4 ; -2,5] ; [2 ; t] mit t ≠ 2; [3 ; 3 + h] mit h > 0.
3. Gegeben ist die Funktion f(x) = \frac{3}{4}x^2 - 3x .
a) Berechne die mittlere Änderungsrate von f(x) auf dem Intervall I = [ 2 ; 5 ]!
b) Bestimme die Gleichung der Sekante s(x) durch P ( 2 | f(2) ) und Q ( 5 | f(5) )!
c) Berechne die momentane Änderungsrate von f(x) an der Stelle x = 2!
d) Zeichne die Graphen von f(x) und s(x) in ein Koordinatensystem!
4. Freier Fall
Beim freien Fall bewegt sich ein Körper so, dass er in der Zeit t den Weg s(t) = 5 \cdot t^2 zurücklegt (s in Meter, t in Sekunden).
Bestimme seine momentane Geschwindigkeit zu den Zeiten t = 1; 2; 3.
5. Ein Pudding kühlt nach seiner Zubereitung ab.
Der Term T(t) = 20 + 70e^{-0,1t} ; t \geq 0 (t in Minuten, T(t) in Grad Celsius) beschreibt den Abkühlungsvorgang. Die Abbildung zeigt den Graphen der Funktion T(t).
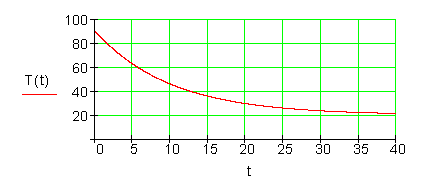
a) Von welcher anfänglichen Temperatur geht man aus?
b) Welche Temperatur hat der Pudding, wenn er abgekühlt ist?
c) Zu welcher Zeit ist die Geschwindigkeit, mit der sich der Pudding abkühlt am größten?
d) Berechne für die ersten 10 Minuten die durchschnittliche Temperaturänderung!
Dazu findest du hier die Lösungen.
Und hier die Theorie: Steigung und Tangente.
Hier findest du eine Übersicht über alle Beiträge zum Thema Differentialrechnung, darin auch Links zu weiteren Aufgaben.

