Bei diesen Aufgaben zur Differentialrechnung VI sollst du folgende Fragen beantworten:
- Funktionen dreimal ableiten.
- In welchem Punkt hat f(x) eine Tangente mit der Steigung
- Bestimme die Gleichung der Tangente an f(x) im Punkt P ( 2 | f(2) ).
- Bestimme die Gleichung der Normalen an f(x) im Punkt P ( 2 | f(2) ).
- Zeichne f(x), Tangente und Normale in ein Koordinatensystem.
Viel Erfolg!
1. Leite folgende Funktionen dreimal ab.
1a) f(x) = 5x^4 - 4x^3 + 3x^2 - 2x + 6
1b) f(x) = (a^2 + x^2)(a^2 - x^2)
1c) f(x) = -2x^4 + 3x^2 - 4x + 2
1d) f(x) = 0,5x^4 - x^3 + 2,5x^2 - 8
1e) f(x) = \frac{1}{32}x^3 + \frac{3}{2}x - 4
1f) f(x) = -\frac{5}{6}x^2 + \frac{2}{3}x + \frac{5}{2}
2.
2a) f(x) = -(x - 6)^2(x + 1)
2b) f(x) = \frac{1}{2}(x^2 - 2)^2
2c) f(x) = \frac{1}{16}(x^3 + x - 1)
2d) f(x) = x(x^2 - \frac{3}{2}x - 4)
2e) f(x) = ax^4 + bx^2 + c
2f) f(x) = ax^3 + bx^2 + cx + d
3.
3a) f(x) = \frac{k}{2}x^4 - 2kx^3 + k^2
3b) f(x) = \frac{1}{k}x^3 + kx^2 + (k a + 1)x
3c) f(x) = \frac{1}{4}x^3 + ax^2 + (a - \frac{1}{2})x - 3
3d)
3e)
3f)
4.
4a)
4b)
4c)
4d)
4e)
4f)
4g)
4h)
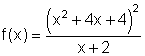
5.
Gegeben ist die Funktion f(x) = 2x - \frac{1}{4}x^2 ; x \in \mathbb{R} .
5a) Bestimme die Steigung von f(x) an der Stelle x_0 mit x_0 \in [-4 ; -1 ; 0 ; 1,5 ; 3]
5b)
In welchem Punkt hat f(x) eine Tangente mit der Steigung 3?
5c)
Bestimme die Gleichung der Tangente an f(x) im Punkt P ( 2 | f(2) ).
5d)
Bestimme die Gleichung der Normalen an f(x) im Punkt P ( 2 | f(2) ).
5e)
Zeichne f(x), Tangente und Normale in ein Koordinatensystem.
5f) g(x) = t \cdot f(x) ; t \in \mathbb{R} schneidet die x-Achse in S_1 und S_2 . Für welche Werte von t sind die Tangenten in S_1 und S_2 orthogonal zueinander?
Hier findest du die Lösungen
und hier die Theorie: Ableitungen höherer Ordnung.
Hier findest du eine Übersicht über alle Beiträge zum Thema Differentialrechnung, darin auch Links zu weiteren Aufgaben.
