Hier findest du die Lösungen der Aufgaben zur Differentialrechnung VI. Du sollst Funktionen dreimal ableiten, bei der 5. Aufgabe sollst du Tangente und Normale berechnen.
Dazu kannst du dir das 📽️Video Differentiationsregeln: Potenzregel, Konstantenregel, Summenregel ansehen.
1. a) Leite folgende Funktionen dreimal ab!
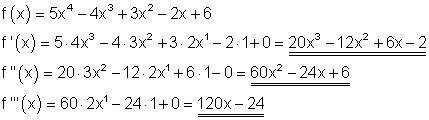
1. b)

1. c)
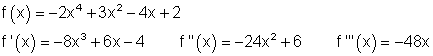
1. d)
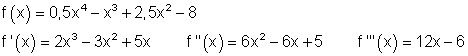
1. e)
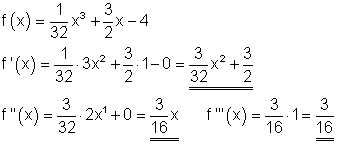
1. f)
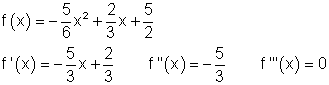
2. a) Leite folgende Funktionen dreimal ab!

2. b)

2. c)
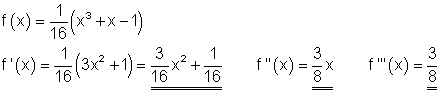
2. d)
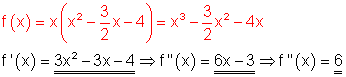
Die Anwendung der Produktregel wäre hier zu aufwendig.
2. e)
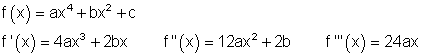
2. f)
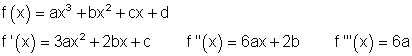
3. a) Leite folgende Funktionen dreimal ab!
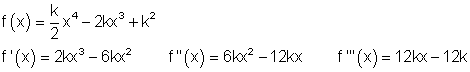
3. b)
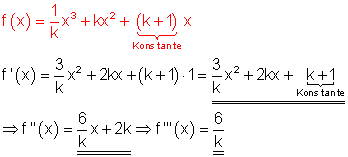
3. c)
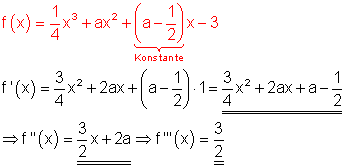
3. d)

3. e)
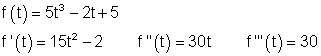
3. f)
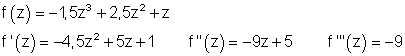
4. a) Leite folgende Funktionen dreimal ab!
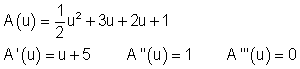
4. b)
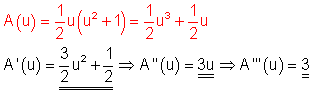
Die Anwendung der Produktregel wäre hier zu aufwendig.
4. c)
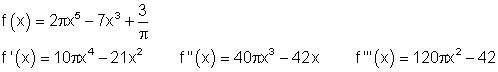
4. d)

Die Quotientenregel sollte nur in den Fällen angewendet werden, wenn sich der Funktionsterm auf andere Art nicht vereinfachen lässt.
4. e)
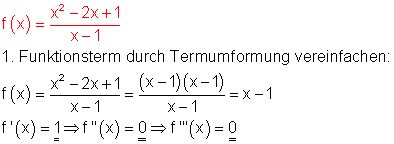
Auf die Anwendung der Quotientenregel wird verzichtet.
4. f)
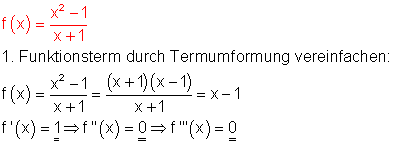
Auf die Anwendung der Quotientenregel wird verzichtet.
4. g)
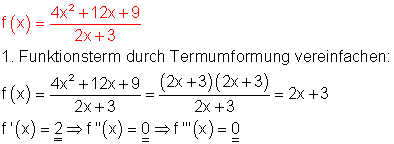
Auf die Anwendung der Quotientenregel wird verzichtet.
4. h)

Auf die Anwendung der Quotientenregel wird verzichtet.
5. Gegeben ist die Funktion
f(x) = 2x - \frac{1}{4}x^2 ; x \in \mathbb{R} .
5. a) Bestimme die Steigung von f(x) an der Stelle x_0 mit x_0 \in [-4 ; -1 ; 0 ; 1,5 ; 3]
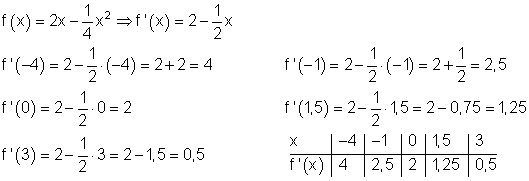
5. b)
In welchem Punkt hat f(x) eine Tangente mit der Steigung 3?
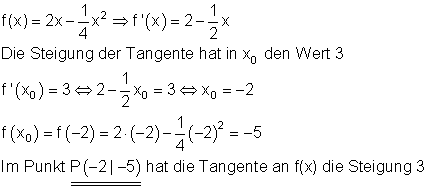
5. c)
Bestimme die Gleichung der Tangente an f(x) im Punkt P ( 2 | f(2) ).
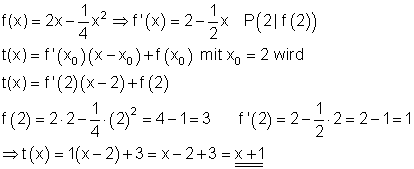
5. d)
Bestimme die Gleichung der Normalen an f(x) im Punkt P ( 2 | f(2) ).
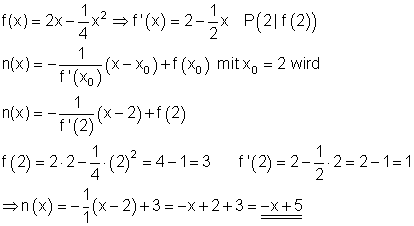
5. e)
Zeichne f(x), Tangente und Normale in ein Koordinatensystem.
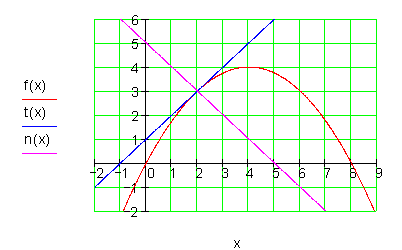
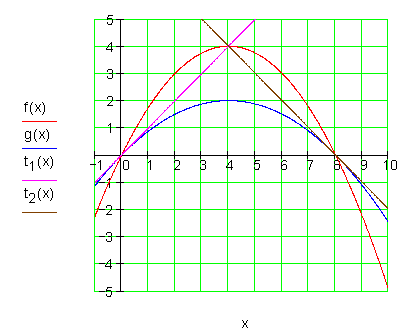
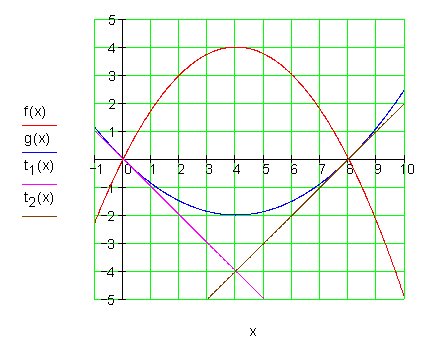
5. f) g(x) = t \cdot f(x) ; t \in \mathbb{R} schneidet die x-Achse in S_1 und S_2 . Für welche Werte von t sind die Tangenten in S_1 und S_2 orthogonal zueinander?
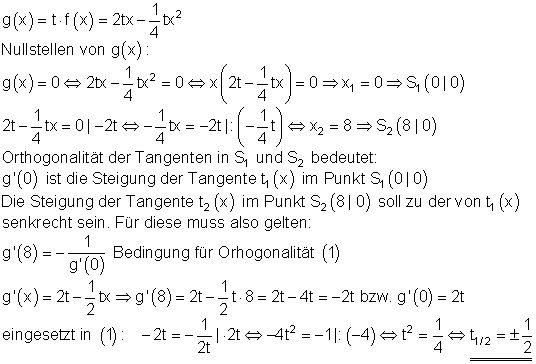
![]()
![]()
Hier findest du die Aufgaben
und hier die Theorie: Differentialquotient und Ableitung.
Hier findest du eine Übersicht über alle Beiträge zum Thema Differentialrechnung, darin auch Links zu weiteren Aufgaben.

