Hier findet ihr weitere Parameteraufgaben zur Differential- und Integralrechnung II. Anforderungen sind dabei: Achsenschnittpunkte, Extremwerte, Wendepunkte, Nullstellen.
1. Parameteraufgaben zur Differenzialrechnung und Integralrechnung
![]()
a) Berechne, falls vorhanden, die Achsenschnittpunkte.
b) Berechne, falls vorhanden, die Extrempunkte.
c) Berechne, falls vorhanden, die Wendepunkte.
d) Bestimme die Funktionswerte für die Grenzen des Definitionsbereichs.
e) Bestimme die Fläche Ak zwischen den Achsenschnittpunkten und der x-Achse.
f) Fertige eine Wertetabelle für x ∈ (-5; -4; …;4; 5) an und zeichne die Graphen für k ∈ (1; 2; 3; 4) in ein Koordinatensystem.
g) Berechne die Funktionsgleichungen folgender Ortskurven:
fokh (x) Ortskurve der Hochpunkte von fk (x) und
fokw (x) Ortskurve der Wendepunkte von fk (x) und zeichne diese in das Koordinatensystem.
h) Berechne für k = 4 die Fläche A4 und kennzeichne diese im Koordinatensystem.
2. Aufgabe
![]()
a) Berechne, falls vorhanden, die Achsenschnittpunkte. Für welche Werte von k gibt es Nullstellen?
b) Berechne die ersten drei Ableitungen von fk (x).
c) Untersuche fk (x) auf Extremstellen und machen eine Aussage über die Art des Extremums in Abhängigkeit von k.
d) Untersuche fk (x) auf Wendestellen in Abhängigkeit von k.
e) Die Fläche Ak zwischen den Nullstellen und der x- Achse soll in Abhängigkeit von k berechnet werden.
![]()
f) Zeichne die Graphen für k ∈ (-4; -2; 0; 2; 4) in ein Koordinatensytem.
Verwende die Daten aus folgender Wertetabelle:
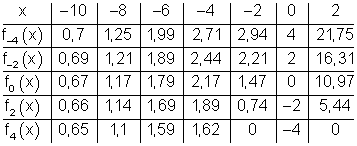
Berechne zusätzlich, falls erforderlich, die Nullstellen, Extrempunkte und die Wendepunkte.
g) Berechne den Flächeninhalt von A4 und kennzeichne diese Fläche im Koordinatensystem.
Dazu findest du hier die ausführlichen Lösungen.
Und hier die dazugehörige Theorie: Differentations- und Integrationsregeln.
Hier findest du eine Übersicht über weitere Beiträge zur Fortgeschrittenen Differential- und Integralrechnung, darin auch Links zu weiteren Aufgaben.

