Hier findest du die Lösungen der Aufgaben Kurvendiskussion mit dem graphikfähigen Taschenrechner GTR Casio fx-CG20 und Casio fx-CG50. Dies hier ist eine Ergänzung der Lösungen, die du hier findest.
Eine Einführung in den Casio fx-CG20 und Casio fx-CG50 findest du hier.
Dort findest du auch eine Anleitung, wie man den Casio fx-CG20 auf den Casio fx-CG50 updaten kann.
Als erstes möchte ich die wesentlichen Schritte einer Kurvendiskussion ganzrationaler Funktionen kurz wiederholen:
- Falls nicht gegeben, die Funktionsgleichung f(x) aufstellen.
- Die Achsenschnittpunkte berechnen.
- Extremwerte berechnen.
- Wendepunkt und Wendetangente bestimmen.
- Eine Wertetabelle aufstellen mithilfe der man den Graphen zeichnen kann.
- Graphen von f(x) und t(x) in ein geeignetes Koordinatensystem zeichnen.
Aufgabe:
Der Graph einer ganzrationalen Funktion 3. Grades verläuft durch die Punkte:
a)
Die allgemeine Funktionsgleichung einer ganzrationalen Funktion 3. Grades lautet:
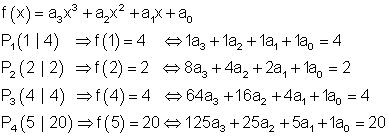
So sieht die Eingabeprozedur aus:
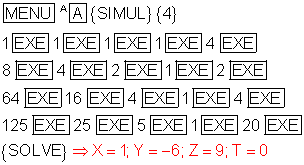
Das bedeutet: a3 = 1 , a2 = -6 , a1 = 9 , a0 = 0
Somit lautet die Funktionsgleichung:
![]()
e)
Berechnen Sie die Extrempunkte!
Die Grafik der Funktion können Sie im Betrachtungsfenster aufrufen.
Mit S[Sketch] {Cls} können Sie den Graph neu zeichnen lassen.
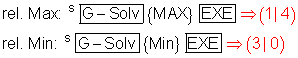
Mit [EXIT] gelangt man zurück in den Grafikeditor.
f)
Berechnen Sie den Wendepunkt und die Wendetangente!
Falls nicht bereits geschehen, stellen Sie Derivative wird auf On,
damit später die Gleichung der Wendetangente angezeigt werden kann.
![]()
Im Grafikeditor trägt man unterhalb von Y1 f‘ und f“ wie folgt ein:
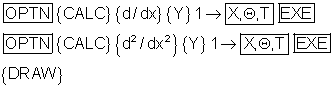
Betrachtungsfenster auf y: [ -4 ; 5 ] mit gleicher Skalierung einstellen.
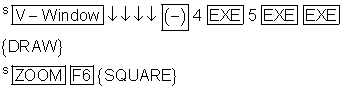
Die Wendestelle liegt dort, wo die zweite Ableitung Null ist.
![]()
Die Wendestelle liegt bei xw = 2.
Der zugehörige Wendepunkt hat die Koordinaten:
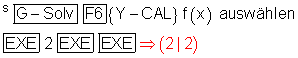
Wendetangente:
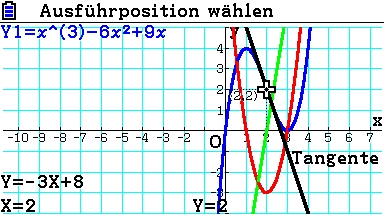
An der Stelle xw = 2 wird die Tangente an f(x) gebildet.
![]()
Wendetangente: t(x) = -3x + 8
Die Farbe der Wendetangente soll auf schwarz geändert werden:
![]()
g)
Berechnen Sie die Achsenschnittpunkte!
So geben Sie Funktionsgleichung mit dem Grafikeditor ein:
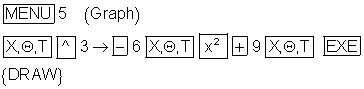
Um den Graphen optimal anzuzeigen, stellen Sie das Betrachtungsfenster auf
y: [ -2 ; 5 ] mit gleicher Skalierung für beide Achsen ein.
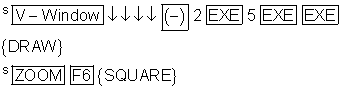
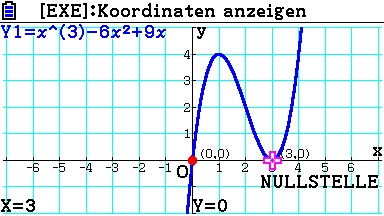
Schnittpunkt mit der y-Achse:
![]()
Nullstelle oder Schnittpunkt mit der x-Achse:
![]()
Py ( 0 | 0 ) und Px1 ( 0 | 0) ; Px2/3 ( 3 | 0) ist doppelte Nullstelle, da Berührungspunkt.
Wertetabelle erstellen
Für das Intervall [ -1 ; 4 ] soll eine Wertetabelle mit der Schrittweite 0,5 erstellt werden.
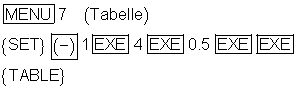
Wertetabelle (gerundet auf 2 Stellen):
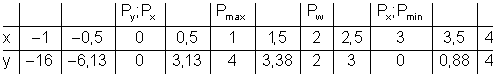
h)
Graph
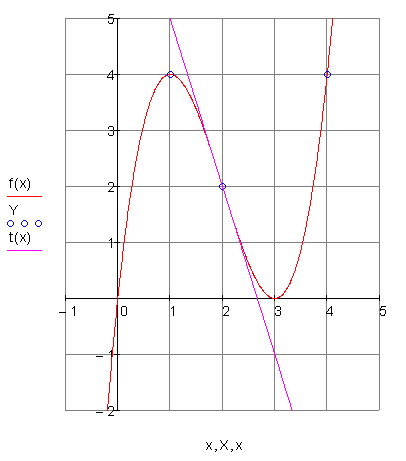
Hier findest du Aufgaben.
Und hier die Lösungen zu Fuß.
Hier die Theorie: Kurvendiskussion mit Beispielen.
Außerdem hier weitere Beispiele, auch mit dem grafikfähigen Taschenrechner: Kurvendiskussion Beispiel 1.
und hier noch weitere Aufgaben aus der Praxis.
Hier findest du eine Übersicht über alle Beiträge zum Thema Differentialrechnung.
Weitere Beispiele zu dem Casio fx-CG20 finden Sie in der Kategorie GTR
und in der Übersicht über alle Beiträge zum grafikfähigen Taschenrechner Casio fx-CG20.

