Hier findest du die Lösungen der Aufgaben zur Kurvendiskussion ganzrationaler Funktionen I.
a) Ausführliche Lösung:
Zuerst stellen wir die Funktionsgleichung aus den vorgegebenen Punkten auf.

b)
Da ganzrationale Funktionen auf ganz IR definiert sind, ist die maximale Definitionsmenge von f(x) = x3 – 6x2 + 9x D = ℝ.
c)
Der Summand von f(x) mit der höchsten Potenz hat Einfluss auf den Verlauf des Graphen.
Für f(x) = x3 – 6x2 + 9x gilt: Verlauf von III -> I.
Das bedeutet, der Graph beginnt im 3. Quadranten und endet im 1. Quadranten. Für den Verlauf dazwischen, kann man zunächst noch keine Aussage treffen.
d)
Da die Summanden von f(x) sowohl gerade als auch ungerade Exponenten besitzen, ist der Graph von f(x) weder punkt-, noch achsensymmetrisch.
e)
Extrempunkte:
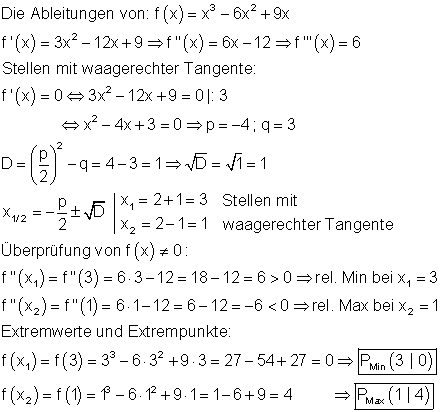
f)
Wendepunkt und Wendetangente:

g)
Achsenschnittpunkte:
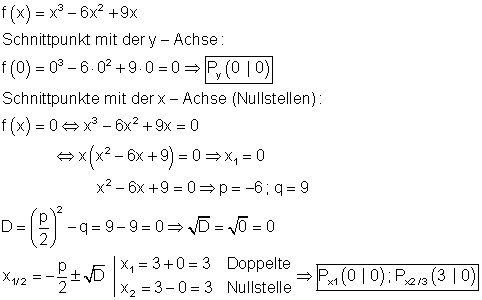
h)
Tabelle aller bisher bekannten Werte:
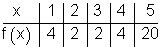
Sollten zum Zeichnen des Graphen noch Werte fehlen, sind diese zu berechnen.
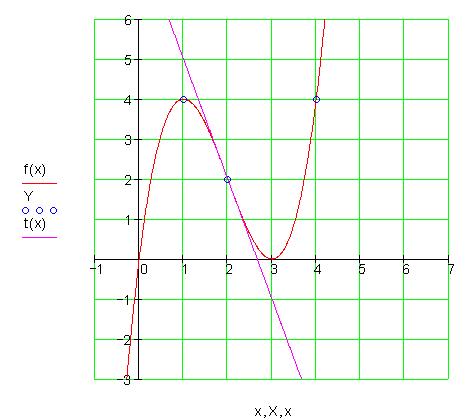
i)
Aus dem Graphen lässt sich das Krümmungs- und Monotonieverhalten ablesen.

j)
Randpunkte des Definitionsbereichs:
Zu untersuchen ist das Verhalten von f(x) für sehr große und sehr kleine x- Werte.
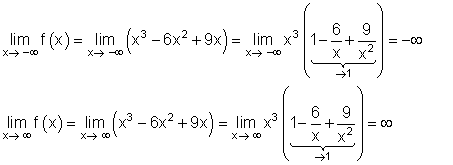
Die Werte in den Klammerausdrücken streben für sehr große und für sehr kleine x- Werte gegen den Wert 1. Das hat zur Folge, dass der Term x3 den Verlauf des Graphen für große und kleine x- Werte näherungsweise bestimmt.
Hier findest du die Lösungen mit dem Casio fx-CG 20 und Casio fx-CG 50.
Und hier sind die Aufgaben.
Hier die Theorie: Kurvendiskussion mit Beispielen.
Außerdem hier weitere Beispiele, auch mit dem grafikfähigen Taschenrechner: Kurvendiskussion Beispiel 1.
Und hier noch weitere Aufgaben aus der Praxis.
Hier findest du eine Übersicht über alle Beiträge zum Thema Differentialrechnung.

