Hier stelle ich eine Extremwertaufgabe mit einem Rechteck unter einer Parabel vor. Für welche Werte von a und b hat das Rechteck dabei den größten Flächeninhalt? Den Lösungsansatz erkläre ich in einem Video. Im Beitrag Aufgaben Differential- und Integralrechnung III findet ihr eine Aufgabe dazu.
Extremwertaufgabe Rechteck unter einer Parabel Lösungsansatz:
Für welche Werte von a und b hat das Rechteck den größten Flächeninhalt? Außerdem: Wie groß ist dieser?
Den Lösungsansatz erkläre ich ausführlich in diesem 📽️Video Extremwert Rechteck Parabel.
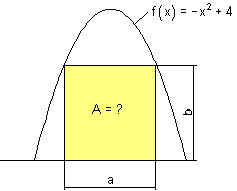
Bei Textaufgaben ist es immer gut, als erstes zu fragen:
Was haben wir?
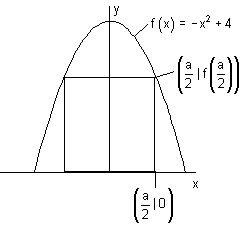
Zuerst die Formel zur Berechnung eines Rechtecks. A = a \cdot b
Also schauen wir uns an, wie die beiden Seiten a und b mit der Funktion f(x)= -x^2+4 zusammenhängen.
Die Funktion spiegelt sich in der y-Achse. Das heißt, die y-Achse halbiert das Rechteck. Und damit auch die Länge a. Die rechte untere Seite des Rechtecks hat folglich die Koordinaten (\frac{a}{2}|0) .
Die rechte obere Ecke des Rechtecks hat also die Koordinaten (\frac{a}{2}|f(\frac{a}{2})) .
Mit anderen Worten: b hat die Länge b = f(\frac{a}{2}) .
Wenn wir unsere Funktion f(x)= -x^2+4 hier einsetzen, ergibt b= =-(\frac{a}{2})^2+4 = -\frac{a^2}{4}+4 .
Danach können wir dies in die Formel zur Berechnung eines Rechtecks einsetzen: A = a \cdot b = a \cdot [-\frac{a^2}{4}+4] =\color{red}-\frac{a^3}{4}+4a .
Den Lösungsansatz erkläre ich ausführlich in diesem 📽️Video Extremwert Rechteck Parabel.
Als nächstes fragen wir uns:
Was suchen wir?
Extremwertaufgabe Rechteck unter einer Parabel Berechnung:
Für welches a hat die Rechteckfläche ihr Maximum? Mit anderen Worten, wir suchen das Maximum der Funktion a=\frac{a^3}{4}+4a . Das heißt, wir berechnen den Extremwert. Das Maximum dieser Funktion ist da, wo die Steigung am größten ist. Also die 1. Ableitung gleich Null. Außerdem die 2. Ableitung ungleich Null. Das könnt ihr hier ausführlich nachlesen: Extrempunkte berechnen. Außerdem könnt ihr euch die Videos 📽️ Video Extrempunkte in der Differentialrechnug und 📽️ Video Extrempunkte hinreichende Bedingung ansehen.
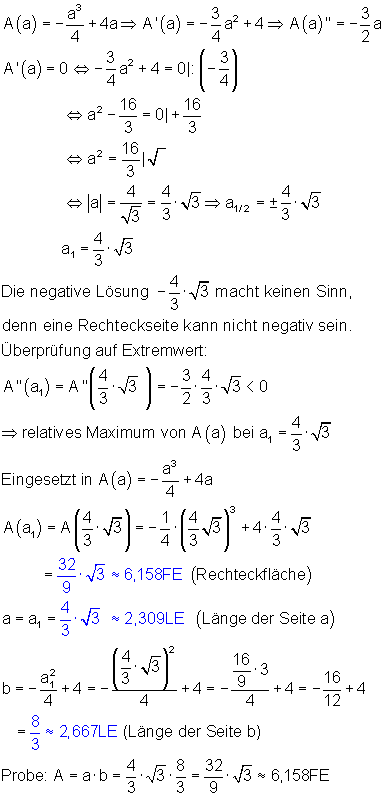
Hier findest du die dazugehörige Theorie: Differentations- und Integrationsregeln.
Und hier eine Übersicht über weitere Beiträge zur Fortgeschrittenen Differential- und Integralrechnung, darin auch Links zu weiteren Aufgaben.

