In diesem Beitrag findet ihr Aufgaben zur Differentialrechnung und Integralrechnung III aus der Praxis. Anforderungen dabei sind:Scheitelpunkt, Extremwerte, Bestimmtes Integral, Wurzelgesetze, e-Funktionen, Potenzgesetze, Logarithmengesetze, Exponentialgleichungen, Mittelwert, bestimmtes Integral, Extremwerte, Integration durch Substitution.
1. Giebelwand
In einer parabelförmigen Giebelwand soll ein rechteckiges Fenster eingelassen werden, das bis zum Boden reicht. Giebelmaße dabei sind: Breite = 4 Meter, Höhe = 4 Meter. Dazu könnt ihr euch das 📽️Video Extremwert Rechteck Parabel ansehen.
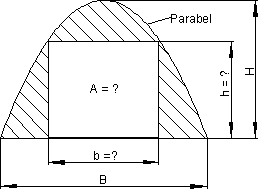
a) Welche Breite und Höhe muss das Fenster haben, damit die Fensterfläche so groß wie möglich wird? Wie groß ist dann die Fläche?
Wennn ihr wissen wollt, wie man die Funktion der Parabel findet: Anwendungsaufgaben quadratische Funktionen. Den Lösungsansatz dazu könnt euch in dem 📽️Video Quadratische Funktion Laster Lösungsansatz ansehen.
Danach hilft euch die Extremwertaufgabe 1 das größte Rechteck zu finden. Dazu könnt ihr euch das 📽️Video Extremwert Rechteck Parabel ansehen.
b) Die restliche Fläche der Giebelwand soll anschließend gestrichen werden. Wie groß ist dann diese Fläche?
Anforderungen dabei sind: Scheitelpunkt, Extremwerte, Bestimmtes Integral, Wurzelgesetze.
2. Bakterienkultur
Eine Bakterienkultur wächst exponentiell. Innerhalb von 48 Stunden hat sich die Zahl der Bakterien von 5000 auf 100000 vermehrt. ( t bzw. x , Zeit in Stunden)
a) Bestimme die Wachstumsfunktion dazu.
b) Innerhalb welcher Zeit verdoppelt sich die Anzahl der Bakterien?
c) Bilde danach den Mittelwert der Bakterienanzahl über die ersten 80 Stunden.
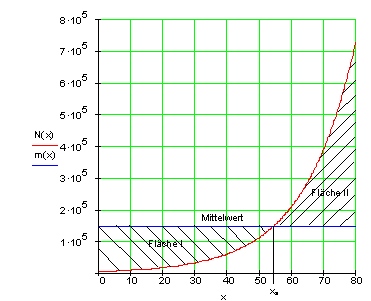
d) In nebenstehender Grafik ist der Verlauf des Graphen der Wachstumsfunktion N(x) und deren Mittelwert m(x) abgebildet. Zeige, dass beide gekennzeichneten Flächen gleich groß sind. Erkläre anschließend, warum das so sein muss.
Anforderungen: e-Funktionen, Potenzgesetze, Logarithmengesetze, Exponentialgleichungen, Mittelwert, bestimmtes Integral.
3. Gegeben ist die Funktion
![]()
Bestimme: die Achsenschnittpunkte, den Tiefpunkt, außerdem den Wendepunkt. Berechne danach die gekennzeichnete Fläche.
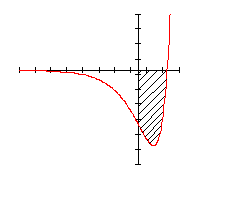
Anforderungen: Exponentialgleichungen, Extremwerte, Integration durch Substitution.
Dazu findest du hier die ausführlichen Lösungen.
Und hier die dazugehörige Theorie: Differentations- und Integrationsregeln.
Hier findest du eine Übersicht über weitere Beiträge zur Fortgeschrittenen Differential- und Integralrechnung, darin auch Links zu weiteren Aufgaben.

