In diesem Beitrag findet ihr die ausführlichen Lösungen zu den Aufgaben zur Differentialrechnung und Integralrechnung III aus der Praxis. Anforderungen: Scheitelpunkt, Extremwerte, Bestimmtes Integral, Wurzelgesetze, e-Funktionen, Potenzgesetze, Logarithmengesetze, Exponentialgleichungen, Mittelwert, bestimmtes Integral, Extremwerte, Integration durch Substitution.
1. Ausführliche Lösungen:
Dazu könnt ihr euch das 📽️Video Extremwert Rechteck Parabel ansehen.
Mathematisierung des Problems
Allgemein:
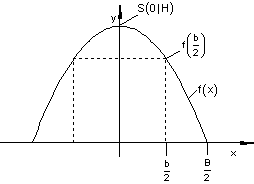
Speziell für B = 4 m, H = 4 m
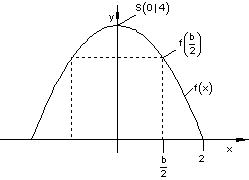
a)
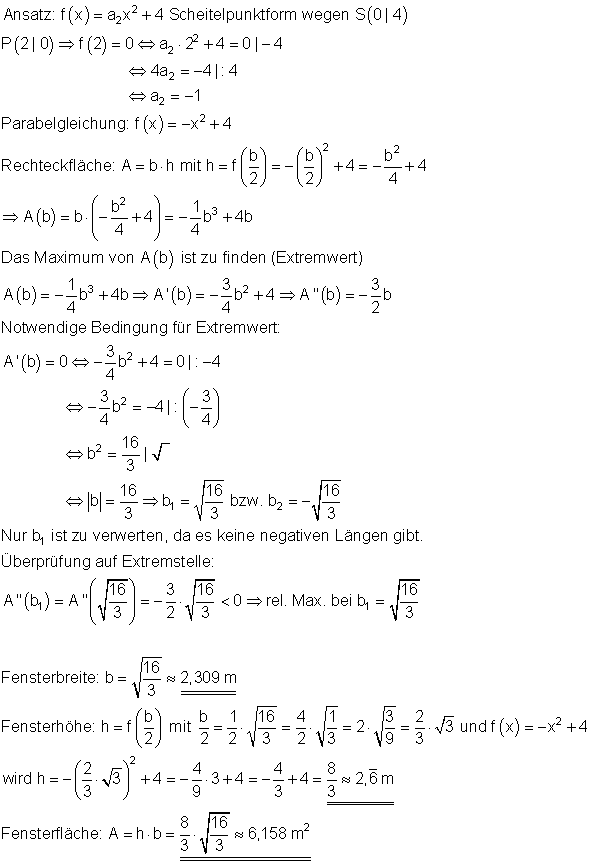
b)

2. Ausführliche Lösungen:
a)

b)
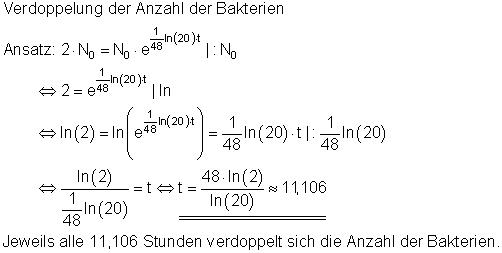
c)
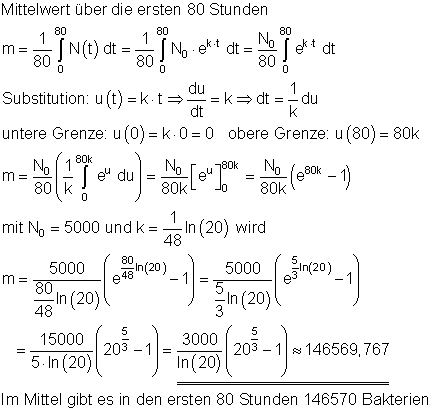
d)

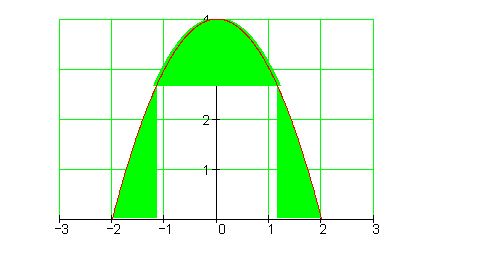
Die Funktion m(x) = m bildet den Mittelwert der Wachstumsfunktion N(x). Der Teil der Fläche (Fläche I), der unterhalb von m(x) liegt, muss genauso groß sein wie der Teil der Fläche (Fläche II), der oberhalb von m(x) liegt. Das folgt aus dem Mittelwert. Da nun N(x) im Bereich von Fläche I unterhalb von m(x) liegt, ist dort der Wert des Integrals negativ. Da N(x) im Bereich von Fläche II oberhalb von m(x) liegt, ist dort der Wert des Integrals positiv. Bei Flächengleichheit muss demzufolge der Wert des Integrals über den gesamten Bereich, der gemittelt wurde, gleich Null sein. Obige Rechnung zeigt, das dies der Fall ist.
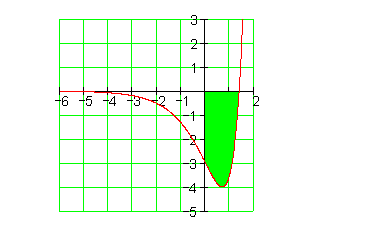
3. Ausführliche Lösung:
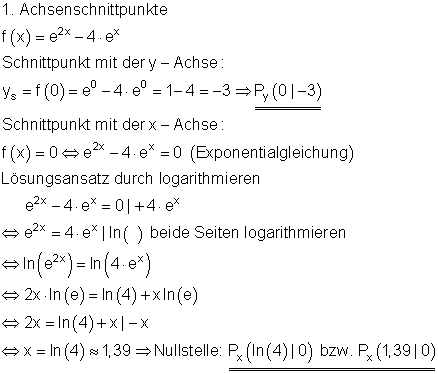

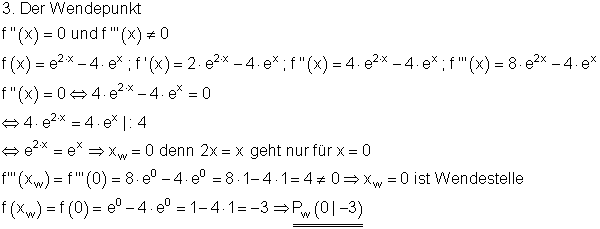
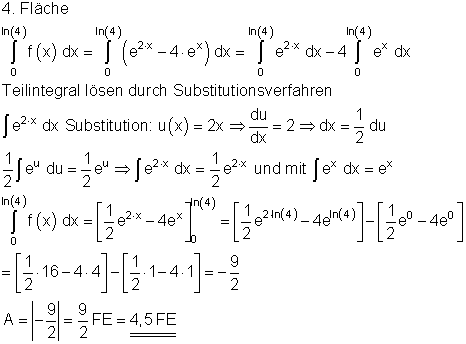
Hier findest du die Aufgaben.
Und hier die dazugehörige Theorie: Differentations- und Integrationsregeln.
Hier findest du eine Übersicht über weitere Beiträge zur Fortgeschrittenen Differential- und Integralrechnung, darin auch Links zu weiteren Aufgaben.

