Anwendungsaufgaben quadratischen Funktionen I

Hier findest du Textaufgaben und Anwendungsaufgaben zu quadratischen Funktionen Teil I.

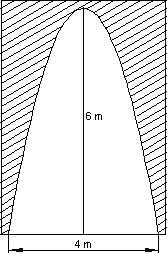
1. Eine Tordurchfahrt hat die Form einer Parabel.

Sie ist 6 m hoch und 4 m breit.
Ein Fahrzeug ist 3 m breit und 2,20 m hoch.
Kann dieses Fahrzeug die Tordurchfahrt passieren?
Hinweis:
Berechne zuerst die Funktionsgleichung des Parabelbogens.

Das ist eine komplexe Aufgabe, deshalb erkläre ich sie in drei Videos:
Als Erstes erkläre ich den Lösungsansatz: Wie geht man bei einer Textaufgabe vor? Wie forme ich den Text um, damit ich eine weiß, was ich rechnen muss?
📽️Video Quadratische Funktion Laster Lösungsansatz

 

Als nächstes erstellen wir aus den Punkten die Funktion:
📽️Video Quadratisch Funktion symmetrisch erstellen aus 2 Punkten

Schließlich können wir mithilfe der Funktion berechnen, ob der Laster durchs Tor passt:
📽️ Video Quadratisch Funktion Textaufgabe Laster passt

2. Ein Bogenschütze

schießt einen Pfeil senkrecht in die Höhe. Die Höhe h des Pfeils in Abhängigkeit von der Zeit t wird beschrieben durch:

a) Löse die Gleichung h(t) = 0 und erläutere die Bedeutung der Lösungen.
b) Zeichne den Graphen von h(t).
c) Nach welcher Zeit hat der Pfeil wieder die Abschusshöhe ( h = 2 ) erreicht?
d) Berechne die größte Höhe, die der Pfeil erreicht.

3. Eine Parabel

Dadurch entsteht jeweils eine neue Parabel.
Gib den zugehörigen Funktionsterm an, wenn es sich um folgende Abbildungen handelt:
a) Spiegelung an der x- Achse.
b) Spiegelung an der y- Achse.
c) Verschiebung um 3 Einheiten in Richtung der positiven x- Achse.
d) Verschiebung um 2 Einheiten in Richtung der negativen y- Achse.
e) Streckung mit dem Faktor 4 in y-Richtung.

4. Der Gewinn einer Unternehmung

in Abhängigkeit von der hergestellten Menge ist eine ganzrationale Funktion 2. Grades.
Bei 50 ME ist der Gewinn Null, für 150 ME ist der Gewinn maximal.
Er beträgt dann 60000 €.
Bestimme den Funktionsterm der Gewinnfunktion.

5. Eine parabelförmige Bogenbrücke

hat eine Spannweite von 223 Metern. Ein Wanderer will die Höhe der Brücke bestimmen. Im Abstand von 1,2 Metern zum Fußpunkt der Brücke (durch Fußschrittmessung) ist der Brückenbogen 2,0 Meter hoch (durch Vergleich mit der Körpergröße).
a) Welche Höhe hat der Brückenbogen maximal?
b) Um wie viel Prozent ändert sich die ermittelte Brückenhöhe, wenn der Wanderer bei der Fußschrittmessung 10 Zentimeter weniger gemessen hätte?