Hier findest du die Lösungen mit komplettem Lösungsweg der Aufgaben zu Parabeln aus gegebenen Bedingungen I.
1. Ausführliche Lösung
f(x) = x^2 + a_1x + a_0
Bedingung für keine Nullstelle: D < 0
p = a_1; \, q = a_0 \Rightarrow D = (\frac{p}{2})^2 - q = (\frac{a_1}{2})^2 - a_0 = \frac{a_1^2}{4} - a_0
D < 0 \Leftrightarrow \frac{a_1^2}{4} - a_0 < 0 \, \, | +a_0
\Leftrightarrow \frac{a_1^2}{4} < a_0 \, \, | \cdot 4
\Leftrightarrow \underline{\underline{a_1^2 < 4a_0}}
2. Ausführliche Lösung
f(x) = -x^2 + 1; \, g(x) = ax^2 - a
g(x) = f(x) \Leftrightarrow ax^2 - a = -x^2 + 1 \Leftrightarrow (a + 1)x^2 - (a + 1) = 0
Betrachtung von a :
\underline{\underline{a = -1}} \Rightarrow f(x) = g(x) identische Parabel mit unendlich vielen Schnittpunkten
\underline{\underline{a \neq -1}} \Rightarrow (a + 1)x^2 - (a + 1) = 0 \Leftrightarrow x^2 = 1
\Rightarrow x_{1 / 2} = \pm 1 zwei verschiedene Schnittpunkte
3. Ausführliche Lösungen
a)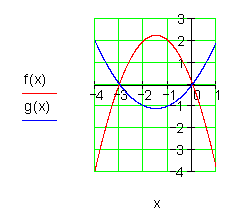
f(x) = -x^2 - 3x = -x(x + 3)
\Rightarrow P_{x_1}(0 | 0); \, \, P_{x_2}(-3 | 0)
g(x) = 0,5x(x + 3)
\Rightarrow P_{x_1}(0 | 0); \, \, P_{x_2}(-3 | 0)
f(x) und g(x) haben die gleichen Nullstellen:
f(x): \, S(-1,5 | 2,25)
g(x) = -0,5 \cdot f(x)
\Rightarrow y_s = -0,5 \cdot 2,25 = - 1,125
\Rightarrow S(-1,5 | -1,125)
b)
Einsetzen von x = u in die Funktionsgleichungen ergibt die y-Werte:
f(u) = -u^2 - 3u \Rightarrow \underline{\underline{P(u | -u^2 - 3u)}}
g(u) = 0,5u(u + 3) \Rightarrow \underline{\underline{Q(u | 0,5u(u + 3))}}
c)
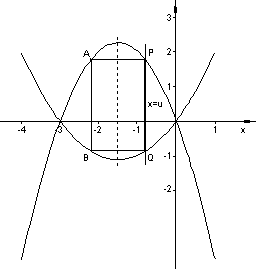
Ergebnis aus b)
P(u | -u^2 - 3u) oder P(u | -u(u + 3) )
Q(u | 0,5u(u + 3))
x-Koordinaten des Scheitels x_s = -1,5
Für u gilt:
-3 \le u \le 0 \Rightarrow u ist negativ
\overline{PQ} = \vert{\underbrace{-u}_{+}\underbrace{(u + 3)}_{+}} \vert + \vert \underbrace{0,5u}_{-}\underbrace{(u + 3)}_{+} \vert
\Rightarrow \overline{PQ} = -u(u + 3) - 0,5u(u + 3)
\overline{PQ} = -1,5u(u + 3)
\overline{AP} = \overline{BQ}
Falls \underline{-1,5 \le u \le 0} ( x = u liegt rechts vom Scheitel)
dann gilt \frac{\overline{AP}}{2} = \vert -1,5 \vert - \vert u \vert = 1,5 + u (da u negativ) \Rightarrow AP = 2(1,5 + u)
Rechteckfläche: A = \overline{PQ} \cdot \overline{AP} = -1,5u(u + 3) \cdot 2(1,5 + u)
Speziell für u = -1 gilt: A = -1,5 \cdot (-1)(-1 + 3) \cdot 2(1,5 -1) = \underline{\underline{3FE}}
Der Umfang des Rechtecks in Abhängigkeit von u:
U = 2(\overline{PQ} + \overline{AP}) = 2[ -1,5u(u + 3) + 2(1,5 + u)] = \underline{\underline{-3u^2 - 5u +6}}
Falls \underline{-1,5 \le u \le 0} ( x = u liegt links vom Scheitel)
dann gilt: \frac{\overline{AP}}{2} = \vert u \vert - \vert -1,5\vert = -u -1,5 (da u negativ) \Rightarrow AP = 2(-u - 1,5)
Der Umfang des Rechtecks in Abhängigkeit von u:
U = 2(\overline{PQ} + \overline{AP}) = 2[-1,5u (u + 3) + 2(-u -1,5)] = \underline{\underline{-3u^2 - 13u -6}}
d)
f(x) = -x^2 - 3x; \, \, g(x) = 0,5x(x + 3) = 0,5x^2 + 1,5x
Die in y-Richtung verschobene Parabel g(x) hat die Funktionsgleichung:
g^*(x) = 0,5x^2 + 1,5x + a_0 (x-Wert des Scheitels bleibt x_s = 1,5 )
Bedingung für die Berührung beider Parabeln:
f(x) = g^*(x) und D = 0
f(x) = g^*(x) \Leftrightarrow x^2 + 3x + \frac{2}{3}a_0 = 0 \Rightarrow p = 3; \, \, q = \frac{2}{3}a_0 \Rightarrow D = \frac{9}{4} - \frac{2}{3}a_0
D = 0 \Leftrightarrow a_0 = \frac{27}{8} = 3,375 \Rightarrow g^*(x) = 0,5x^2 + 1,5x + 3,375
Berührungspunkt: B(-1,5 | g^*(-1,5)) \Rightarrow B(-1,5 | 2,25)
Die Parabel g(x) wird um \underline{\underline{3,375 LE }} nach oben geschoben und berührt f(x) in \underline{\underline{B(-1,5 | 2,25)}}
e)
f(x) = -x^2 - 3x
f(a) = -a^2 - 3a
f(a + 1) = -(a +1)^2 -3(a + 1) = -a^2 -5a -4
f(a) - f(a+1) = 4 \Leftrightarrow -a^2 - 3a - (-a^2 - 5a - 4) = 4
\Leftrightarrow 2a + 4 = 4 \Leftrightarrow \underline{\underline{a = 0}}
4. Ausführliche Lösung
f(x) = (x - 1)(x - 2) = x^2 - 3x +2; \, \, g(x) = ax^2
f(x) = g(x) \Leftrightarrow (1 - a)x^2 - 3x + 2 = 0; \, \, mit a \neq 1
\Leftrightarrow x^2 - \frac{3}{1 - a}x + \frac{2}{1 - a} = 0 \Rightarrow p = - \frac{3}{1 - a}; \, \, q = \frac{2}{1 - a}
Bedingung für Berührung ist D = 0
\Rightarrow D = (\frac{p}{2})^2 - q = ( - \frac{3}{2(1 - a)})^2 - \frac{2}{1 - a} = 0
\Leftrightarrow \frac{9}{4(1 - a)^2} - \frac{2}{1 - a} = 0 \Leftrightarrow \frac{9}{4(1 - a)^2} - \frac{8(1 - a)}{4(1 - a)^2} = 0
\Leftrightarrow 9 - 8(1 - a) = 0 \Leftrightarrow a = - \frac{1}{8}
\underline{\underline{g(x) = - \frac{1}{8}x^2}} berührt \underline{\underline{f(x)}}
5. Ausführliche Lösung
Normalparabel g(x) = x^2; \, \, f(x) = ax^2 + 1
f(x) = g(x) \Leftrightarrow x^2 = - \frac{1}{a - 1} für a \neq 1
für a > 1 \Rightarrow x^2 = - \frac{1}{a - 1} < 0 \Rightarrow keine Lösung
für a < 1 \Rightarrow x^2 = - \frac{1}{a - 1} > 0 \Rightarrow zwei Lösungen x_{1/2} = \pm \sqrt{- \frac{1}{a - 1}}
6. Ausführliche Lösung
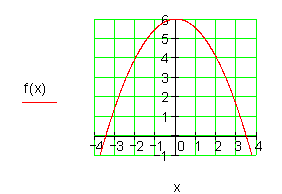
S(0 | 6) \Rightarrow f(x) = a_2x^2 + 6
P_x(2 \sqrt{3} | 0)
\Rightarrow f(2 \sqrt{3}) = a_2(2 \sqrt{3})^2 + 6 = 0
\Leftrightarrow 12a_2 + 6 = 0 \Leftrightarrow a_2 = - \frac{1}{2}
\Rightarrow \underline{\underline{f(x) = - \frac{1}{2}x^2 + 6}}
Dazu kannst du dir dieses 📽️Video Quadratisch Funktion symmetrisch erstellen aus 2 Punkten ansehen.
7. Ausführliche Lösung
f(x) = a_2(x - k)(x + 2) Linearfaktoren
f(0) = -k \Leftrightarrow a_2(-k)(2) = - k \Rightarrow a_2 = \frac{1}{2}
\Rightarrow f(x) = \frac{1}{2}(x - k)(x + 2) = \underline{\underline{\frac{1}{2}[x^2 + (2 - k)x - 2k]}}
8. Ausführliche Lösung
f(x) = a_2x^2 + a_1x + 3; \, \, g(x) = 2x - 1
g(-1) = -2 - 1 = -3 \Rightarrow f(-1) = -3 \Leftrightarrow a_2 - a_1 + 3 = -3
g(0,5) = 1 - 1 = 0 \Rightarrow f(0,5) = 0 \Leftrightarrow 0,25a_2 + 0,5a_1 + 3 = 0
\Rightarrow a_2 = -8; \, \, a_1 = -2
\underline{\underline{f(x) = -8x^2 - 2x + 3}}
Hier findest du die Aufgaben.
Und hier die dazugehörige Theorie: Zusammenfassung Quadratische Funktionen.
Außerdem eine Übersicht über weitere Beiträge zu quadratische Funktionen, darin auch Links zu weiteren Aufgaben.
