Hier findest du die Lösungen zu den Textaufgaben und Anwendungsaufgaben zu quadratischen Funktionen Teil I mit komplettem Lösungsweg.
1. Torbogen
Was haben wir?
Eine Parabel mit drei Punkten:
Der Torbogen ist 6 Meter hoch, der Scheitelpunt der Parabel hat also die Koordinaten S (0 | 6). Das heißt a0 = 6.
Das ist eine komplexe Aufgabe, deshalb erkläre ich sie in drei Videos:
Als Erstes erkläre ich den Lösungsansatz: Wie geht man bei einer Textaufgabe vor? Wie forme ich den Text mathematisch um:
📽️Video Quadratische Funktion Laster Lösungsansatz
Die Mitte des Torbogens läuft durch die y-Achse, deshalb gibt es hier keine Verschiebung auf der x-Achse. Daher haben wir kein alleine stehendes x, folglich a1 = 0.
Der Torbogen ist 4 Meter breit, also jeweils 2 Meter rechts und links von der y-Achse. Damit kennen wir die Punkte auf der x-Achse: P1 (-2 | 0) und P2 (2 | 0).
Somit haben wir bereits: f(x) = a2 x2 + 6.
Was suchen wir?
Der Laster ist 2,2 Meter hoch. Er passt durch das Tor, wenn es in dieser Höhe breiter als 3 Meter ist. Wir suchen also den Punkt P3, von dem die y-Koordinate den Wert 2,2 hat, also P3 (? | 2,2).
Wenn der x-Wert von diesem Punkt größer als 3 ist, dann kann der Laster hindurch fahren.
Funktion aufstellen:
Um a2 zu berechnen, setzen wir die Werte eines dieser Punkte ein:
f(x) = a_2 x^2 + 6
f(2) = 0 \Rightarrow a_2 \cdot 2^2 + 6 = 0 | - 6
\Leftrightarrow a_2 \cdot 4 = - 6 | : 4
\Leftrightarrow a_2 = \dfrac{- 6}{4} = - \dfrac{3}{2}
Damit haben wir die Funktion: - \dfrac{3}{2} x^2 + 6
Dazu kannst du dir dieses 📽️Video Quadratisch Funktion symmetrisch erstellen aus 2 Punkten ansehen.
Als nächstes prüfen wir, ob der Laster durch das Tor fahren kann.
Er ist 2,2 Meter hoch, das entspricht dem Wert auf der y-Achse. Deshalb berechnen wir den x-Wert dazu:
- \dfrac{3}{2} x ^2 + 6 = 2,2 |-6
\Leftrightarrow - \dfrac{3}{2} x ^2 = 2,2 - 6 | \cdot \dfrac{2}{3}
\Leftrightarrow x ^2 = -3,8 \cdot -\dfrac{2}{3} | \sqrt{}
\Leftrightarrow x = \sqrt2,53 = 1,59
Das ist nur die halbe Breite des Torbogens, deshalb multiplizieren wir mit 2 und erhalten 3,18 m. Der Laster ist 3 Meter breit, also kann er durch das Tor fahren.
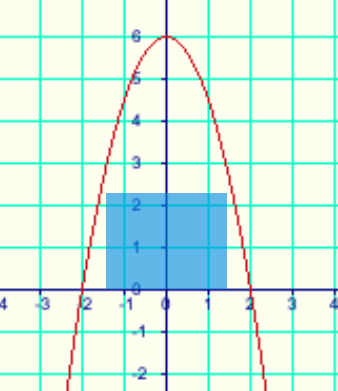
Schließlich können wir mithilfe der Funktion berechnen, ob der Laster durchs Tor passt:
📽️ Video Quadratisch Funktion Textaufgabe Laster passt
2. Bogenschütze
a)
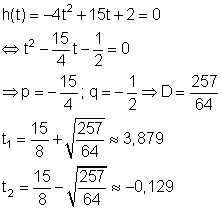
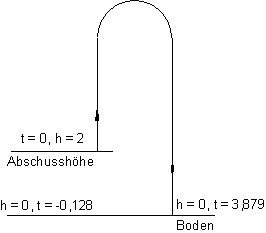
Bedeutung der beiden Lösungen:
Zur Zeit t = 0 wird der Pfeil von einer Höhe h = 2 m abgeschossen.
Nach der Zeit t = 3,879 s kommt der Pfeil auf dem Boden h = 0 an.
Würde man den Pfeil vom Boden h = 0 aus abschießen, so benötigt er für die ersten 2 m die Zeit 0,128 s.
b)
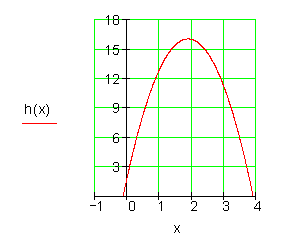
c)
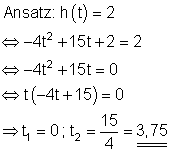
Nach t = 3,75 s befindet sich der Pfeil wieder auf der Abschusshöhe von 2 m.
d)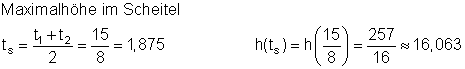
Die größte Höhe 16,063 m wird nach 1,875 s erreicht.
3. Parabel
a)![]()
b)
c)![]()
d)![]()
e)![]()
4. Der Gewinn einer Unternehmung
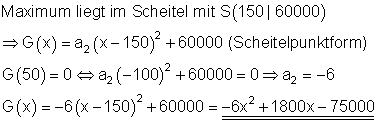
5. Eine parabelförmige Bogenbrücke
a)Die Länge des gesamten Brückenbogens beträgt s = 223 m.
Die y-Achse teilt den Bogen in zwei Hälften, so dass der rechte Fußpunkt bei v = 111, 5 m liegt.
Im ersten Fall ist der Abstand vom Fußpunkt 1,2 m, er liegt also bei
u = 111,5 m – 1,2 m = 110,3 m.
Dort hat der Brückenbogen eine Höhe von 2 m.
Da der Abstand vom Fußpunkt im 2. Fall nur noch 1,1 m betragen soll, ist es sinnvoll, die Rechnung zunächst mit den Variablen u und v allgemein durchzuführen. Die konkreten Werte werden zuletzt eingesetzt.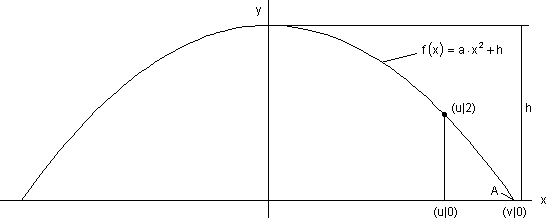

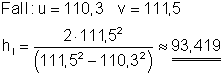
b)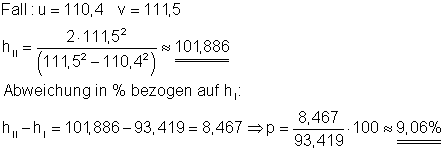
Der Brückenbogen hat im Fall I eine Höhe von etwa hI = 93,419 m.
Im Fall II beträgt die Höhe etwa hII = 101,886 m.
Der prozentuale Unterschied bezogen auf hI beträgt etwa 9,06%.
Hier findest du die Aufgaben.
Und hier die dazugehörige Theorie: Zusammenfassung Quadratische Funktionen.
Hier eine Übersicht über weitere Beiträge zu quadratische Funktionen, darin auch Links zu weiteren Aufgaben.

