Mit diesen Aufgaben zur Differenzialrechnung und Integralrechnung III kannst du für eine Klassenarbeit üben, auch bei Textaufgaben zur e-Funktion überlege als erstes: Wonach wird gefragt?
1. Aufgaben Differenzialrechnung Bodenschätze
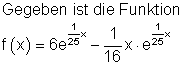
Der Graph von f(x) beschreibt die Förderung von Bodenschätzen. Im Jahre x = 0 (1900) begann man mit der industriellen Förderung. f(x) gibt die geförderte Menge in 1000 Tonnen pro Jahr an.
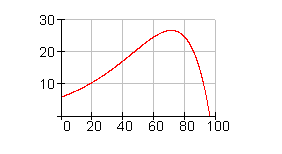
a) Wie hoch war die jährliche Förderung zu Beginn der Aufzeichnungen?
b )In welchem Jahr hat man die Förderung eingestellt?
c) In welchem Jahr war die Förderung maximal? Wie hoch war sie?
d) In welchem Jahr war der Zuwachs der Fördermenge am größten?
e) Wie viel Bodenschätze hat man insgesamt gefördert?
f) Wie hoch war die durchschnittliche Fördermenge?
Anforderungen: Nullstellen, Extremwerte, Wendepunkt, Partielle Integration.
2. Aufgaben Differenzialrechnung und Integralrechnung: Medikament
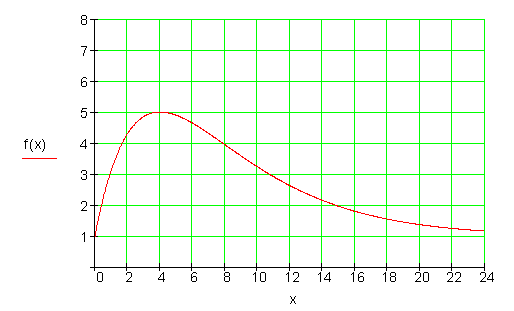
Nach einer Operation erhält ein Patient eine Infusion. Die Abbildung zeigt die Dosierung eines Medikamentes über einen Zeitraum von 24 Stunden. Dosierung bedeutet dabei: Zufuhr pro Zeit in mg/h. Man hat mit einer Dosierung von 1 mg/h begonnen.
a) Beschreibe den Verlauf der Dosierung.
b) Der Verlauf der Dosierung soll mit einer Exponentialfunktion 
modelliert werden. Berechne geeignete Werte für a und k, wenn nach x = 4 Stunden eine maximale Dosierung von 5 mg/h eingestellt ist. Wie lautet die Funktionsgleichung?
c) Zu welchem Zeitpunkt ist die Abnahme der Dosierung am stärksten?
d) Berechne die Menge des verabreichten Medikamentes, wenn man die Infusion 24 Stunden durchgeführt hat.
Aufgaben zur Differenzialrechnung und Integralrechnung mit e-Funktion, Ableitung, Extremwerte, Wendepunkt, partielle Integration, bestimmtes Integral.
3. Aufgaben Differenzialrechnung und Integralrechnung:
Gefriergut
Entnimmt man Gefriergut aus der Kühltruhe, so erwärmt es sich. Der Erwärmungsvorgang lässt sich durch folgende Funktionsgleichung beschreiben:
a) Bis auf welche Temperatur erwärmt sich das Gefriergut maximal?
b) Nach welcher Zeit wird die Temperatur Null Grad Celsius erreicht?
c) Zu welchem Zeitpunkt ist die Temperaturzunahme am größten?
d) Bestimme die durchschnittliche Temperatur für die Zeit von der 30. bis zur 90. Minute.
4. Fläche
Gegeben sind die Funktionen
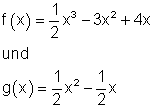
Berechnen Sie die Maßzahl der Fläche, die den Punkt D ( 1 | 1 ) enthält.
5. Wendetangente
a) Zeichne den Graphen für [ -1 ; 5 ] in ein Koordinatensystem.
b) Berechne den Hochpunkt.
c) Berechne den Wendepunkt.
d) Bestimme die Gleichung der Wendetangente.
e) 
6. Wendepunkt
Eine zur y-Achse symmetrische ganzrationale Funktion 4. Grades verläuft durch die
a) Stelle die Funktionsgleichung auf.
b) Bestimme die Achsenschnittpunkte.
c) Berechne die Extremwerte und den Wendepunkt.
d) Zeichne den Graphen.
e) 
Dazu findest du hier die ausführlichen Lösungen.
Und hier eine Übersicht über weitere Beiträge zur Fortgeschrittenen Differential- und Integralrechnung, darin auch Links zur Theorie und zu weiteren Aufgaben.
