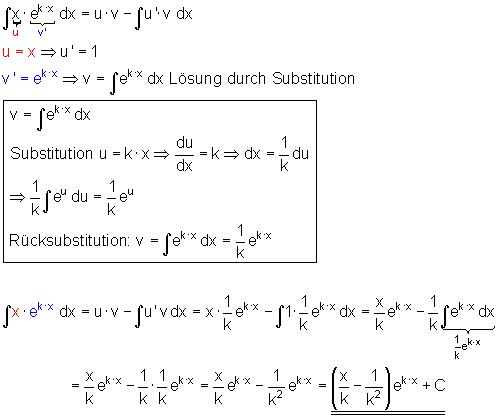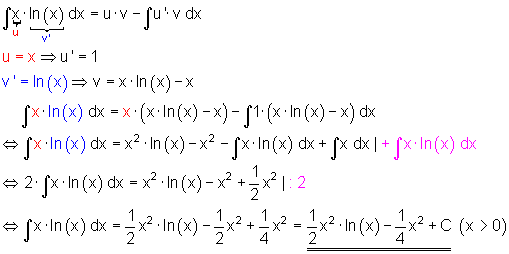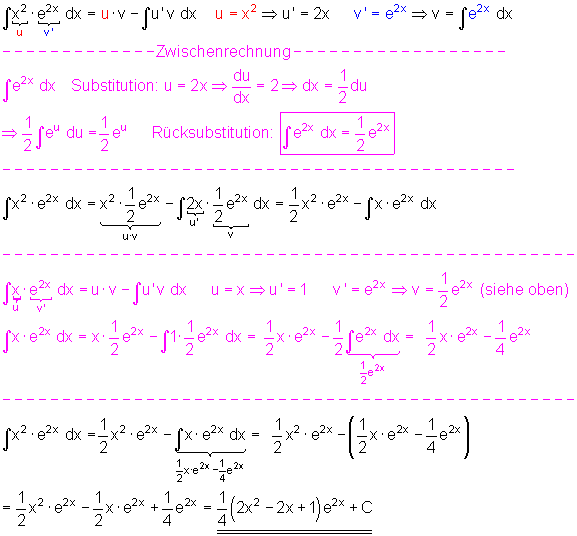Zuerst zeige ich anhand eines anschaulichen Beispiels, dass man das Produkt zweier Funktionen oft nicht integrieren kann. Danach zeige ich eine Möglichkeit, das Produkt zweier Funktionen mittels Produktregel zu integrieren. Zuletzt stelle ich dazu mehrere Beispiele zur Verfügung.
Wenn man das Produkt zweier Funktionen integriert will, so versagen in den meisten Fällen die bisher bekannten Methoden der Integration.
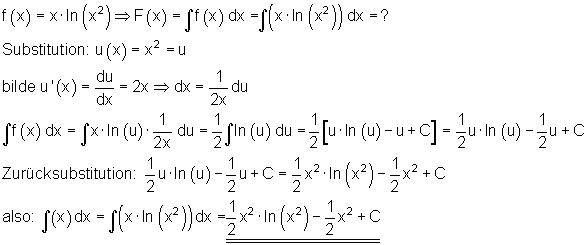
Dieses Integral kann man mit der Methode der Substitution lösen, weil durch die Substitution der Faktor x herausfällt. Das ist normalerweise nicht der Fall.
![]()
Produkt zweier Funktionen mittels Produktregel integrieren
Dieses Integral kann man nicht durch Substitution lösen. Wir entwickeln jedoch aus der Produktregel für die Differentialrechnung einen Ansatz.

Mit Hilfe dieser Umformungen kan man das Integral über ein Produkt zweier Faktoren zwar nicht lösen, aber bei geschickter Wahl von u und v ‚ bzw. von u ‚ und v kan man den Ausdruck so umformen, dass man die Integrale lösen kann.
Beispiele
Die Vorgehensweise zeige ich im folgenden an einigen Beispielen.
1. Beispiel Integration eines Produkts zweier Funktionen:
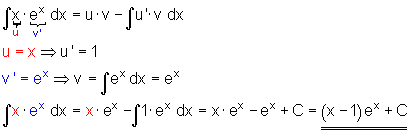
2. Beispiel Integration eines Produkts zweier Funktionen:
3. Beispiel Integration eines Produkts zweier Funktionen:
4. Beispiel:
Dieses Beispiel zeigt, dass man beim Integrieren oftmals mehrere Verfahren nacheinander anwenden muss. Weil die Zwischenergebnisse bei der partiellen Integration oft schon bekannte Integrale sind, die man durch Substitution gefunden hat, sollte man sich diese in Form einer Integraltabelle merken.
Es gibt noch weitere Verfahren und Techniken des Integrierens, auf die ich hier an dieser Stelle nicht eingehen kann. Z. B. die Integration gebrochen rationaler Funktionen mit dem Verfahren der Partialbruchzerlegung.
Hier findest du Aufgaben Integration der e-Funktion, Flächenberechnungen.
Außerdem Aufgaben Werbebanner und vermischte Aufgaben.
Und hier findest du eine Übersicht über weitere Beiträge zur Fortgeschrittenen Differential- und Integralrechnung, darin auch Links zu weiteren Aufgaben.