Hier findest du die Lösungen der Aufgaben zur Klassenarbeit zum Thema quadratische Funktionen im Berufliches Gymnasium Jahrgangsstufe 11 mit komplettem Lösungsweg.
Lösungen der Gruppe A
A 1. Ausführliche Lösungen
A 1. a) Löse folgende quadratische Gleichungen:
\frac{2}{3} x^2 - \frac{2}{3} x - \frac{4}{3} = 0 | : \frac{2}{3} \\
\Leftrightarrow x^2 - x - 2 = 0
\Rightarrow p = -1 ; q = -2 \\
D = (\frac{p}{2})^2 - q \\
= \frac{1}{4} + 2 = \frac{1}{4} + \frac{8}{4} = \frac{9}{4} \\
\Rightarrow \sqrt D = \sqrt{\frac{9}{4}} = \frac{3}{2}
x_{1/2} = -\frac{p}{2} \pm \sqrt D
x_1 = \frac{1}{2} + \frac{3}{2} = \frac{4}{2} = \underline{\underline{2}}
x_2 = \frac{1}{2} - \frac{3}{2} = -\frac{2}{2} = \underline{\underline{ -1}}
A 1. b)
(\frac{1}{2} x - 2) \cdot (\frac{3}{4} x + 2) = 0
Lösung mit dem Satz vom Nullprodukt.
\frac{1}{2} x - 2 = 0 | + 2 \Leftrightarrow \frac{1}{2} x = 2 | \cdot 2 \\
\Leftrightarrow x = 4 \Rightarrow \underline{\underline{x_1 = 4}}
\frac{3}{4} x + 2 = 0 | - 2 \Leftrightarrow \frac{3}{4} x = - 2 | : \frac{3}{4}
\Leftrightarrow x = -\frac{2}{1} : \frac{3}{4} = -\frac{8}{3} \Rightarrow \underline{\underline{x_2 = - \frac{8}{3} }}
A 2.
Gegeben sind die Funktionsgleichungen zweier Parabeln und deren Nullstellen.
A 2. a)
a) Berechne die Scheitelpunkte S1 und S2 beider Parabeln.
f_1(x) = x^2 + 4x + 3
Die Nullstellen sind: x_1 = -3 ; x_2 = -1 \\
x_s = \dfrac{x_1 + x_2}{2} = \frac{-3 - 1}{2} = - 2 \\
y_s = f_1(x_s) = f_1(-2) = 4 - 8 + 3 = -1 \\
\Rightarrow \underline{\underline{S_1(-2 | -1)}}
x_1 = -1 ; x_2 = 3 \\
x_s= \dfrac{x_1 + x_2}{2} = \frac{-3 - 1}{2} =
f_2(x) = \frac{1}{2} x^2 - x - \frac{3}{2}
Die Nullstellen sind: x_1 = -1 ; x_2 = 3 \\
x_s = \dfrac{x_1 + x_2}{2} = \frac{-1 +3}{2} = 1 \\
y_s = f_2(x_s) = f_2(1) = \frac{1}{2} - 1 - \frac{3}{2} = - 2 \\
\Rightarrow \underline{\underline{S_2 = (1 | -2) }}
A 2. b)
b) Berechne die Scheitelpunktform der Funktionsgleichungen f1(x) und f2(x).
f_1(x) = a_2 (x - x_s)^2 + y_s = \underline{\underline{(x + 2)^2 - 1 }}
f_2(x) = a_2 (x - x_s)^2 + y_s = \underline{\underline{\frac{1}{2} (x - 1)^2 -2 }}
A 2. c)
c) Bestimme durch Rechnung die Funktionsgleichung g(x) der Geraden, die durch beide Scheitelpunkte verläuft.
g(x) = a_1x + a_0 mit S_1(-2 | -1) und S_2(1 | -2) als P_1 und P_2
a_1 = \dfrac{y_2 - y_1}{x_2 - x_1} = \frac{-2 - (-1)}{1 - (-2)} = \frac{-2 +1}{1 + 2} = -\frac{1}{3} \\
\Rightarrow g(x) = -\frac{1}{3}x + a_0\\
S_2(1 | -2) \Rightarrow g(1) = -2 \\
\Leftrightarrow -\frac{1}{3} \cdot 1 + a_0 = -2 | + \frac{1}{3} \\
\Leftrightarrow a_0 = -\frac{5}{3} \\
\Rightarrow \underline{\underline{g(x) = -\frac{1}{3}x - \frac{5}{3} }}
A 2. d)
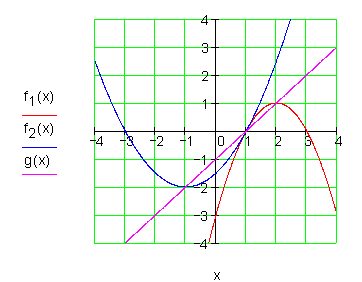
d) Zeichne beide Parabeln und die Gerade in ein Koordinatensystem!
A 3. Ausführliche Lösungen
Der Benzinverbrauch eines PKW in Liter/100 km in Abhängigkeit von der Geschwindigkeit v in km/h lässt sich durch folgende Funktionsgleichung beschreiben:
b(v) = 0,0005 v^2 - 0,05 v + 8 für v > 40
Hinweis: Die Funktionsgleichung b(v) ist die Gleichung einer nach oben geöffneten Parabel.
Schreibe zu jedem Ergebnis einen Antwortsatz!
A 3. a)
Berechne den Verbrauch bei einer Geschwindigkeit von 140 km/h.
b(v) = 0,0005 v^2 - 0,05 v + 8 für v > 40
b(140) = 0,0005 \cdot 140^2 - 0,05 \cdot 140 + 8 = \underline{\underline{10,8}}
Bei einer Geschwindigkeit von 140 km/h beträgt der Benzinverbrauch 10,8 Liter auf 100 km.
A 3. b)
Bei welcher Geschwindigkeit beträgt der Verbrauch genau 8 Liter auf 100 km?
b(v) = 8 \Leftrightarrow 0,0005 v^2 - 0,05 v + 8 = 8 | -8
0,0005 v^2 - 0,05 v = 0 \Leftrightarrow v (0,0005 v - 0,05) = 0 \Rightarrow v_1 = 0 < 40 scheidet aus \\
0,0005 v - 0,05 = 0 | + 0,05 \Leftrightarrow 0,0005 v = 0,05 | : 0,0005 \Leftrightarrow \underline{\underline{v_2 = \frac{0,0005} {0,05} }} = 100
Bei einer Geschwindigkeit von 100 km/h beträgt der Benzinverbrauch 8 Liter auf 100 km.
A 3. c)
Bei welcher Geschwindigkeit ist der Kraftstoffverbrauch am geringsten? Wie hoch ist er genau?
Beim Graphen von b(v) handelt es sich um eine nach oben geöffnete Parabel mit dem Scheitelpunkt S( 50 | 6,75 ). Der Scheitelpunkt ist der tiefste Punkt der Parabel. Das entspricht dem niedrigsten Kraftstoffverbrauch. Bei einer Geschwindigkeit von 50 km/h ist der Kraftstoffverbrauch am geringsten. Er beträgt 6,75 Liter auf 100 km.
A 4.
Gegeben ist die Funktionsgleichung einer Parabel. Begründe jedes Ergebnis durch eine entsprechende Rechnung.
A 4. a) Diskriminante D
f(x) = x^2 + 3x + a_0
f(x) = 0 \Leftrightarrow x^2 + 3x + a_0 = 0 \Rightarrow p = 3 ; q = a_0 \\
D = (\frac{p}{2})^2 - q = (\frac{3}{2})^2 - a_0 = \underline{\underline{\frac{9}{4} - a_0}}
A 4. b) Bedingung für eine Nullstelle:
D = 0 \Leftrightarrow \frac{9}{4} - a_0 = 0 | + a_0
\Leftrightarrow \frac{9}{4} = a_0 \Leftrightarrow a_0 = \frac{9}{4}
Für a_0 = \frac{9}{4} = 2,25 hat f(x) = x^2 + 3x + a_0 also genau eine Nullstelle.
A 4. c) Bedingung für zwei Nullstellen:
D > 0 \Leftrightarrow \frac{9}{4} - a_0 > 0 | + a_0
\Leftrightarrow \frac{9}{4} > a_0 \Leftrightarrow a_0 < \frac{9}{4}
Für a_0 < \frac{9}{4} = 2,25 hat f(x) = x^2 + 3x + a_0 also genau zwei Nullstellen.
A 4. d) Bedingung für keine Nullstelle:
D < 0 \Leftrightarrow \frac{9}{4} - a_0 < 0 | + a_0
\Leftrightarrow \frac{9}{4} < a_0 \Leftrightarrow a_0 > \frac{9}{4}
Für a_0 > \frac{9}{4} = 2,25 hat f(x) = x^2 + 3x + a_0 also keine Nullstellen.
Lösungen der Gruppe B
B 1. Ausführliche Lösungen
a) Löse folgende quadratische Gleichungen:
\frac{2}{3} x^2 + \frac{2}{3} x - \frac{4}{3} = 0 | : \frac{2}{3} \\
\Leftrightarrow x^2 + x - 2 = 0
\Rightarrow p = 1 ; q = -2 \\
D = (\frac{p}{2})^2 - q \\
= \frac{1}{4} + 2 = \frac{1}{4} + \frac{8}{4} = \frac{9}{4} \\
\Rightarrow \sqrt D = \sqrt{\frac{9}{4}} = \frac{3}{2}
x_{1/2} = -\frac{p}{2} \pm \sqrt D
x_1 = -\frac{1}{2} + \frac{3}{2} = \frac{2}{2} = \underline{\underline{1}}
x_2 = -\frac{1}{2} - \frac{3}{2} = -\frac{4}{2} = \underline{\underline{ -2}}
B 1. b)
(\frac{3}{4} x +1) \cdot (2x - \frac{1}{2} ) = 0
Lösung mit dem Satz vom Nullprodukt.
\frac{3}{4} x +1 = 0 | -1 \Leftrightarrow \frac{3}{4} x = -1 | : \frac{3}{4} \\
\Leftrightarrow x = -\frac{1}{1} : \frac{3}{4} = -\frac{4}{3}
\Rightarrow \underline{\underline{x_1 = -\frac{4}{3} }}
2x - \frac{1}{2} = 0 | +\frac{1}{2} \Leftrightarrow 2x = \frac{1}{2} | : 2
\Leftrightarrow x = \frac{1}{2} : \frac{2}{1} = \frac{1}{4} \Rightarrow \underline{\underline{x_2 = \frac{1}{4} }}
B 2. Ausführliche Lösungen
a)
Berechne die Scheitelpunkte S1 und S2 beider Parabeln.
f_1(x) = -x^2 + 4x - 3
Die Nullstellen sind: x_1 = 1 ; x_2 = 3 \\
x_s = \dfrac{x_1 + x_2}{2} = \frac{1 + 3}{2} = 2 \\
y_s = f_1(x_s) = f_1(2) = -4 + 8 - 3 = 1
\Rightarrow \underline{\underline{S_1(2 | 1)}}
f_2(x) = \frac{1}{2} x^2 + x - \frac{3}{2}
Die Nullstellen sind: x_1 = -3 ; x_2 = 1 \\
x_s = \dfrac{x_1 + x_2}{2} = \frac{-3 +1}{2} = -1 \\
y_s = f_2(x_s) = f_2(-1) = \frac{1}{2} - 1 - \frac{3}{2} = - 2 \\
\Rightarrow \underline{\underline{S_2 = (-1 | -2) }}
B 2. b)
Berechne die Scheitelpunktform der Funktionsgleichungen f1(x) und f2(x).
f_1(x) = a_2 (x - x_s)^2 + y_s = \underline{\underline{-(x - 2)^2 + 1 }}
f_2(x) = a_2 (x - x_s)^2 + y_s = \underline{\underline{\frac{1}{2} (x + 1)^2 -2 }}
B 2. c)
Bestimme durch Rechnung die Funktionsgleichung g(x) der Geraden, die durch beide Scheitelpunkte verläuft.
g(x) = a_1x + a_0 mit S_1(2 | -1) und S_2(-1 | -2) als P_1 und P_2
a_1 = \dfrac{y_2 - y_1}{x_2 - x_1} = \frac{-2 - 1}{-1 - 2} = \frac{-3}{-3} = 1 \\
\Rightarrow g(x) = x + a_0\\
S_1(2 | 1) \Rightarrow g(2) = 1 \\
\Leftrightarrow 2 + a_0 = 1 | -2 \\
\Leftrightarrow a_0 = - 1 \\
\Rightarrow \underline{\underline{g(x) = x - 1 }}
B 2. d)
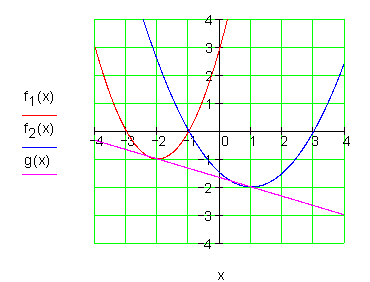
Zeichne beide Parabeln und die Gerade in ein Koordinatensystem!
B 3.
Der Benzinverbrauch eines PKW in Liter/100 km in Abhängigkeit von der Geschwindigkeit v in km/h lässt sich durch folgende Funktionsgleichung beschreiben:
b(v) = 0,0005 v^2 - 0,05 v + 6 für v > 40 .
Hinweis: Die Funktionsgleichung b(v) ist die Gleichung einer nach oben geöffneten Parabel.
Schreibe zu jedem Ergebnis einen Antwortsatz!
B 3. a)
Berechnen Sie den Verbrauch bei einer Geschwindigkeit von 120 km/h.
b(v) = 0,0005 v^2 - 0,05 v + 6 für v > 40
b(120) = 0,0005 \cdot 120^2 - 0,05 \cdot 120 + 6 = \underline{\underline{7,2}}
Bei einer Geschwindigkeit von 120 km/h beträgt der Benzinverbrauch 7,2 Liter auf 100 km.
B 3. b)
Bei welcher Geschwindigkeit beträgt der Verbrauch genau 6 Liter auf 100 km?
b(v) = 6 \Leftrightarrow 0,0005 v^2 - 0,05 v + 6 = 6 | -6
0,0005 v^2 - 0,05 v = 0 \Leftrightarrow v (0,0005 v - 0,05) = 0 \Rightarrow v_1 = 0 < 40 scheidet aus \\
0,0005 v - 0,05 = 0 | + 0,05 \Leftrightarrow 0,0005 v = 0,05 | : 0,0005 \Leftrightarrow \underline{\underline{v_2 = \frac{0,0005} {0,05} }} = 100
Bei einer Geschwindigkeit von 100 km/h beträgt der Benzinverbrauch 6 Liter auf 100 km.
B 3. c)
Bei welcher Geschwindigkeit ist der Kraftstoffverbrauch am geringsten? Wie hoch ist er genau?
Beim Graphen von b(v) handelt es sich um eine nach oben geöffnete Parabel mit dem Scheitelpunkt S( 50 | 4,75 ). Der Scheitelpunkt ist der tiefste Punkt der Parabel. Das entspricht dem niedrigsten Kraftstoffverbrauch. Bei einer Geschwindigkeit von 50 km/h ist der Kraftstoffverbrauch am geringsten. Er beträgt 4,75 Liter auf 100 km.
B 4.
Gegeben ist die Funktionsgleichung einer Parabel. Begründe jedes Ergebnis durch eine entsprechende Rechnung!
B 4. a)
f(x) = x^2 + 5x + a_0
f(x) = 0 \Leftrightarrow x^2 + 5x + a_0 = 0 \Rightarrow p = 5 ; q = a_0 \\
D = (\frac{p}{2})^2 - q = (\frac{5}{2})^2 - a_0 = \underline{\underline{\frac{25}{4} - a_0}}
B 4. b) Bedingung für eine Nullstelle
D = 0 \Leftrightarrow \frac{25}{4} - a_0 = 0 | + a_0
\Leftrightarrow \frac{25}{4} = a_0 \Leftrightarrow a_0 = \frac{25}{4}
Für a_0 = \frac{25}{4} = 6,25 hat f(x) = x^2 + 5x + a_0 also genau eine Nullstelle.
B 4. c) Bedingung für zwei Nullstellen:
D > 0 \Leftrightarrow \frac{25}{4} - a_0 > 0 | + a_0
\Leftrightarrow \frac{25}{4} > a_0 \Leftrightarrow a_0 < \frac{25}{4}
Für a_0 < \frac{25}{4} = 6,25 hat f(x) = x^2 + 5x + a_0 also genau zwei Nullstellen.
B 4. d) Bedingung für keine Nullstelle:
D < 0 \Leftrightarrow \frac{25}{4} - a_0 < 0 | + a_0
\Leftrightarrow \frac{25}{4} < a_0 \Leftrightarrow a_0 > \frac{25}{4}
Für a_0 > \frac{25}{4} = 2,25 hat f(x) = x^2 + 5x + a_0 also keine Nullstellen.
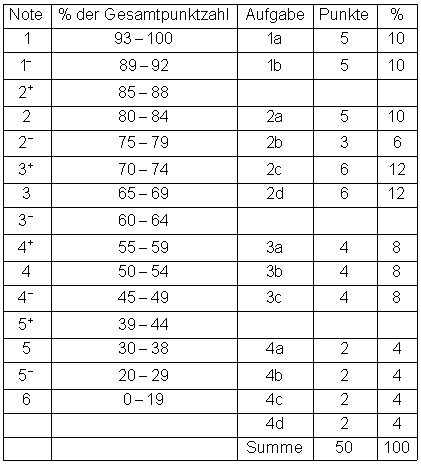
Leistungsbewertung
Hier findest du die Aufgaben.
und hier eine Übersicht über weitere Beiträge zu quadratische Funktionen, darin auch Links zu weiteren Aufgaben.