Nachdem wir die Theorie der Differentialrechnung in mehreren Beiträgen kennengelernt haben, stelle ich hier anhand von Beispielen die Anwendungen in Betriebswirtschaft und Naturwisschenschaft. Zuerst die Betriebswirtschaftliche Anwendungen der Differentialrechnung. Dazu muss ich die Begriffe Kostenfunktion, Differentialkosten und Grenzkosten erläutern. Danach stelle ich die Naturwissenschaftliche Anwendungen der Differentialrechnung vor.
Betriebswirtschaftliche Anwendungen der Differentialrechnung
In der Betriebswirtschaft wird die Differentialrechnung z. B. angewendet, um den geringsten Kostenzuwachs zu berechnen.
Zuerst müssen wir die Kostenfunktion K(x) aufstellen. Sie stellt den Zusammenhang zwischen der Produktionsmenge x und den Gesamtkosten dar. Dazu kannst du dir den Beitrag Kostenrechnung als Anwendung der Differentialrechnung ansehen und das 📽️ Video Kostenfunktion aufstellen ansehen.
Erhöht man die Produktion um Δx, also die Differenz, so erhöhen sich auch die Kosten um ΔK.
Der Differenzenquotient \dfrac{\Delta{K}}{\Delta{x}} beschreibt die durchschnittliche Kostenzunahme bei einer Produktionsänderung von Δx, also die mittlere Änderungsrate.
Die momentane Änderungsrate an der Stelle x0 nennt man Differentialkosten. Sie werden durch den Grenzwert \lim \limits_{\Delta{x}\to 0} \dfrac{\Delta{K}}{\Delta{x}} bestimmt, d. h. durch die Ableitung der Kostenfunktion K.
Im betriebswirtschaftlichen Alltag wird die Differntialrechnung wie folgt angewendet:
Definition:
Die Ableitung der Kostenfunktion K(x) bezeichnet man als Differentialkosten K'(x) oder auch als Grenzkosten K'(x).
Beispiel:
Gegeben ist die Kostenfunktion K(x) = x3 – 9x2 + 40 x + 94
a) Bestimme die Differentialkosten, erstelle dann eine Wertetabelle für K(x) und für K'(x) und zeichne beide Graphen in ein Koordinatensystem.
Dabei sollte die Wertetabelle für I = [ 0 ; 6 ] mit der Schrittweite 1.
b) Bestimme anschließend den geringsten Kostenzuwachs.
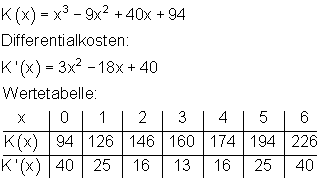
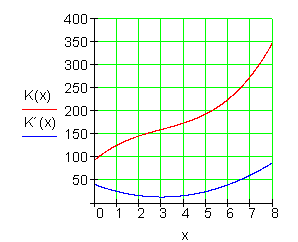
Der geringste Kostenzuwachs liegt im Scheitel der Parabel K'(x), also dort, wo die Tangente an K'(x) waagerecht ist.
K'(x) = 3x2 – 18 x + 40 \Rightarrow K''(x) = 6x - 18
Bedingung für waagerechte Tangente an K'(x):
K''(x) = 0 \Leftrightarrow 6x - 18 = 0 \Rightarrow \underline{\underline{x = 3}}
Das gleiche Ergebnis hätten wir auch aus der Tabelle für K'(x) ablesen können.
Mit anderen Worten: Der geringste Kostenzuwachs entsteht bei einer Ausbringungsmenge von x = 3, dort beträgt er 13 GE / ME.
Dazu kannst du dir das 📽️ Video Extrempunkte in der Differentialrechnug ansehen.
Anwendungen der Differentialrechnung in der Naturwisschenschaft
In der Mathematik betrachtet man meistens Funktionen in Abhängigkeit von der Variablen x.
Dagegen behandelt man in den Naturwissenschaften oft Funktionen in Abhängigkeit von der Zeit t.
Beispiel:
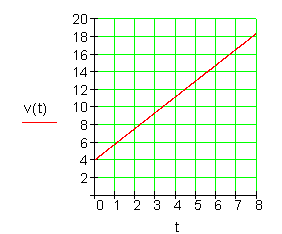
Das Weg-Zeit-Gesetz für einen gleichmäßig beschleunigten Gegenstand mit der Anfangsgeschwindigkeit v_0 = 4\dfrac{m}{s} und \quad der \quad Beschleunigung \quad a = 1,8\dfrac{m}{s^2} lautet:
💡 s(t) = \dfrac{1}{2}at^2 + v_0t 💡
Siehe auch Gleichmäßig beschleunigte Bewegung.




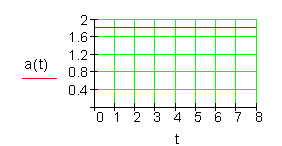
Merke:

Dazu findest du hier die Aufgaben zur Differentialrechnung VII.
Hier findest du eine Übersicht über alle Beiträge zum Thema Differentialrechnung.


