Aufgaben zur Differentialrechnung VIII aus der Praxis

Hier findest du Aufgaben zur Differentialrechnung VIII aus der Praxis. Darin geht es insbesondere um die Kostenrechnung.

Dazu kannst du dir das 📽️ Video Kostenfunktion aufstellen ansehen.

1. Die Gesamtkosten eines Betriebes

werden bei einer maximalen Ausbringungsmenge von 10 Mengeneinheiten (ME) beschrieben durch K(x). Der Verkaufspreis pro ME beträgt 28 GE. K(x) = x³ – 12 x² + 50x + 40.

a) Bestimme die Ableitung der Kostenfunktion (Differentialkostenfunktion oder Grenzkostenfunktion) und zeichne danach den Graphen. Beschreibe anschließend den Graphen.
b) Berechne die minimalen Differentialkosten.
c) Beweise, dass die Differentialkosten für jede Ausbringungsmenge positiv sind.
d) In welchem Bereich kann man mit Gewinn rechnen?
e) In welchem Bereich nimmt der Gewinn zu?

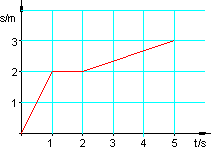
2. Gegeben ist das Weg-Zeit-Diagramm s(t) eines bewegten Körpers.

a) Interpretiere diese Bewegung.
b) Zeichne danach das dazugehörige Geschwindigkeits-Zeit-Diagramm, wenn gilt: v(t) = s'(t).

3. Die Abbildung zeigt den Verlauf einer Bewegung im Weg- Zeit- Diagramm.

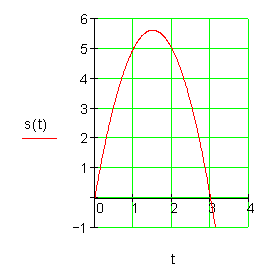
a) Gib ein Beispiel aus dem Alltag an, für das dieser Verlauf zutreffen könnte. Was bedeutet physikalisch der Kurvenverlauf für t > 3?
b) Das Weg-Zeit-Gesetz für diese Bewegung lautet: s(t) = \frac{1}{2}a \cdot t^2 + v_0 \cdot t
Bestimme a und v₀.
c) Zeichne das dazugehörige Geschwindigkeits-Zeit-Diagramm und interpretiere dieses. Welche Bedeutung hat eine negative Geschwindigkeit?

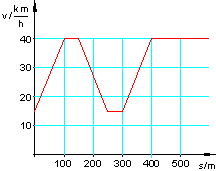
4. Gegeben ist der Geschwindigkeitsverlauf einer Bewegung.

Interpretiere dieses Diagramm.
Mache danach Aussagen über einen möglichen Streckenverlauf.

Dazu findest du hier die Lösungen.

Und hier die Theorie: Differentialrechnung Anwendungen aus Betriebswirtschaft und Naturwissenschaften.

Hier findest du eine Übersicht über alle Beiträge zum Thema Differentialrechnung, darin auch Links zu weiteren Aufgaben.