Hier findest du die Lösungen der Übungen zur Binominalverteilung II.
1.
Eine Familie hat 6 Kinder. Die Wahrscheinlichkeit ein Mädchen zu gebären betrage p = 0,5.
Berechne die Wahrscheinlichkeit dafür, dass unter den 6 Kindern 0, 1, 2, 3, 4, 5, 6 Mädchen sind.
Zeichne außerdem das Histogramm der Wahrscheinlichkeitsverteilung. Bestimme die Wahrscheinlichkeit folgender Ereignisse:
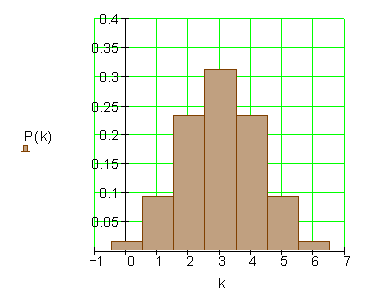
A: Genau die Hälfte der Kinder sind Mädchen.
B: Höchstens die Hälfte der Kinder sind Mädchen.
C: Mindestens die Hälfte der Kinder sind Mädchen.
1. Ausführliche Lösungen
Das Problem kann als 6-stufiger Bernoulli- Versuch betrachtet werden mit n = 6 und p = 0,5. Gesucht ist P(X = k) für k = 0, 1, 2, 3, 4, 5, 6.
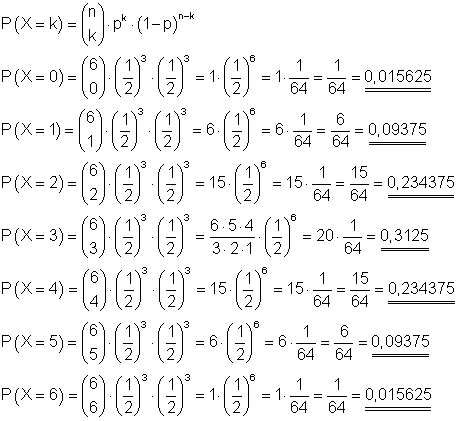
Histogramm der Wahrscheinlichkeitsverteilung:
A:
![]()
ist die Wahrscheinlichkeit dafür, dass unter den 6 Kindern genau drei Mädchen sind.
B:
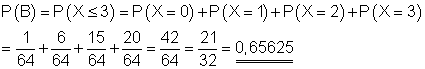
ist die Wahrscheinlichkeit dafür, dass unter den 6 Kindern höchstens drei Mädchen sind.
C:
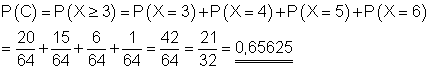
ist die Wahrscheinlichkeit dafür, dass unter den 6 Kindern mindestens drei Mädchen sind.
2.
Eine Münze wird 5 mal geworfen. p sei 0,5.
a) Bestimme die Wahrscheinlichkeitsverteilung der Zufallsvariablen
X: Anzahl der Wappen.
b) Mit welcher Wahrscheinlichkeit wirft man
(1) höchstens 3 mal Wappen?
(2) weniger als 3 mal Wappen?
(3) mindestens 1 mal Wappen?
(4) mehr als einmal Wappen?
2. Ausführliche Lösungen
Das Problem kann als 5-stufiger Bernoulli-Versuch betrachtet werden mit n = 5 und p = 0,5.
a) Gesucht ist P(X = k) für k = 0, 1, 2, 3, 4, 5
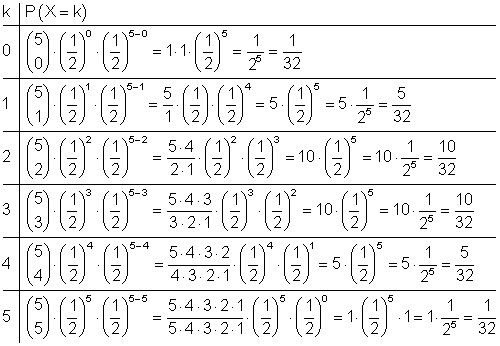
b) (1)Höchstens 3 mal Wappen bedeutet:
![]()
(2) Weniger als 3 mal Wappen bedeutet:
![]()
(3) Mindestens 1 mal Wappen bedeutet:
![]()
(4) Mehr als 1 mal Wappen bedeutet:
![]()
3.
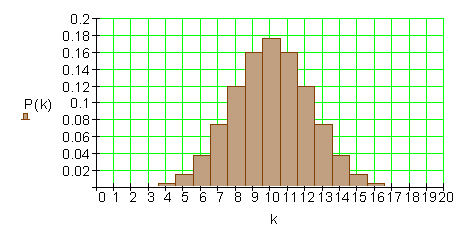
Eine Münze wird 20 mal geworfen.
a) Zeichne das Histogramm der Binomialverteilung.
b) Zu bestimmen sind die Wahrscheinlichkeit für die Ereignisse:
(1) Genau 10 mal Wappen.
(2) Höchstens 15 mal Wappen.
(3) Mindestens 7 mal Wappen.
(4) Mindestens 6 und höchstens 16 mal Wappen.
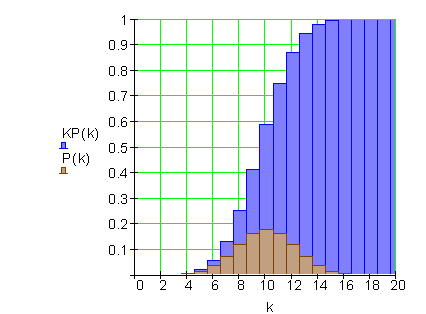
c) Zeichne das Histogramm der kumulierten Wahrscheinlichkeitsverteilung.
3. Ausführliche Lösungen
a) Histogramm der Binomialverteilung für n = 20 und p = 0,5

b) (1)Die Wahrscheinlichkeit P(X = 10) kann aus der Tabelle, bzw. aus dem Histogramm abgelesen werden.
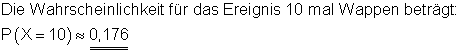
(2) Die Wahrscheinlichkeit für das Ereignis E: Höchstens 15 mal Wappen, kann nicht unmittelbar abgelesen werden. Dazu müssen die Tabellenwerte der Wahrscheinlichkeiten aufaddiert werden.
P(X = 0) + P(X = 1) + … + P(X = 15)
Hat man jedoch eine Tabelle in der die Wahrscheinlichkeiten bereits aufaddiert wurden, also eine kumulierte Tabelle, dann kann man die Wahrscheinlichkeit für E daraus sofort ablesen.
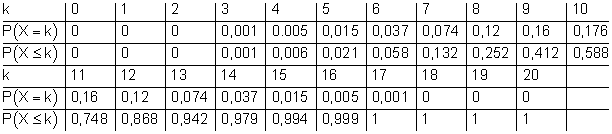
Bemerkung: Für k < 3 ist die kumulierte Wahrscheinlichkeit natürlich nicht Null. Ebenso sind die Werte für k < 20 auch nicht 1. Sie unterscheiden sich aber kaum noch von diesen Werten, so dass man in den meisten Fällen für praktische Berechnungen die gerundeten Tabellenwerte verwenden kann.![]()
(3)
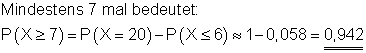
(4)
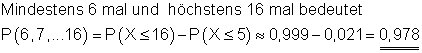
c) Histogramm der kumulierten Wahrscheinlichkeitsverteilung
4.
Ein Multiple-Choice-Test besteht aus 50 Aufgaben mit jeweils 5 Antworten, von denen nur jeweils eine richtig ist. Mit welcher Wahrscheinlichkeit kann man durch bloßes Raten folgende Anzahl von Aufgaben richtig beantworten?
a) Mehr als 20 Aufgaben.
b) Mindestens 10 und höchstens 20 Aufgaben.
c) Weniger als 10 Aufgaben.
d) Genau 15 Aufgaben.
Die Trefferwahrscheinlichkeit pro Aufgabe ist 1/5 = 0,2.
Da diese Wahrscheinlichkeit bei jeder der 50 Aufgaben besteht, kann der Vorgang als 50 stufiger betrachtet werden.
Der Auszug aus der kumulierten Binomialverteilung mit n = 50 und p = 0,2 soll als Hilfestellung genutzt werden.
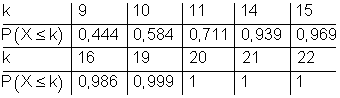
4. Ausführliche Lösungen
a)
![]()
Die Wahrscheinlichkeit durch bloßes Raten mehr als 20 Aufgaben richtig zu beantworten ist kleiner als 0,001 (0,1%).
b)
![]()
Die Wahrscheinlichkeit durch bloßes Raten mindestens 10 und höchstens 20 Aufgaben richtig zu beantworten ist 0,556 (55,6%).
c)
![]()
Die Wahrscheinlichkeit durch bloßes Raten weniger als 10 Aufgaben richtig zu beantworten ist 0,444 (44,4%).
d)
![]()
Die Wahrscheinlichkeit durch bloßes Raten genau 15 Aufgaben richtig zu beantworten ist 0,03 (3%).
Hier findest du die Aufgaben hierzu.
Hier findest du eine Übersicht über alle Beiträge zum Thema Wahrscheinlichkeitsrechnung, darin auch Links zu den Aufgaben Binominalverteilung I und III bis V.
