Hier findest du die Lösungen zur Binominalverteilung mit dem Casio fx-CG50 und Casio fx-CG20. Die Lösung ohne Taschenrechner findest du unter Lösungen zur Binominalverteilung I .

Update auf Casio fx-CG50
3.
Ein Glücksrad hat 3 gleich große Sektoren mit den Symbolen Kreis, Kreuz und Stern. Es wird viermal gedreht. Wie groß ist die Wahrscheinlichkeit für folgende Ereignisse?
A: Es tritt dreimal Stern auf.
B: Es tritt mindestens dreimal Stern auf.
C: Es tritt höchstens einmal Stern auf.
D: Es tritt höchstens dreimal Stern auf.
3. Ausführliche Lösungen
Es handelt sich um einen n = 4-stufigen Bernoulliversuch mit der Erfolgswahrscheinlichkeit p = 1/3.
Rechneraufruf:[MENU] 1 [OPTN] {STAT} {DIST} {BINOMIAL} {Bpd} bzw. {Bcd}
Siehe auch Intervallwahrscheinlichkeit
A: Es tritt dreimal Stern auf bedeutet: P(A) = P(X = 3)
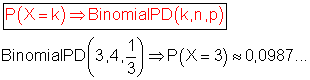
Die Wahrscheinlichkeit dafür, dass genau dreimal Stern auftritt, ist etwa 0,0987…
B: Es tritt mindestens dreimal Stern auf bedeutet: P(B) = P(X ≥ 3)
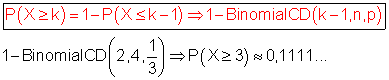
Die Wahrscheinlichkeit dafür, dass mindestens dreimal Stern auftritt, ist etwa 0,1111…
C: Es tritt höchstens einmal Stern auf bedeutet: P(C) = P(X ≤ 1)
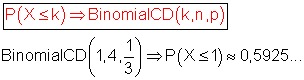
Die Wahrscheinlichkeit dafür, dass höchstens einmal Stern auftritt,ist etwa 0,5925…
D: Es tritt höchstens dreimal Stern auf bedeutet: P(D) = P(X ≤ 3)
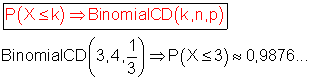
Die Wahrscheinlichkeit dafür, dass höchstens dreimal Stern auftritt, ist etwa 0,9876…
4.
Von einer großen Ladung Apfelsinen sind 20% verdorben. Es werden 5 Stück entnommen. Wie groß ist die Wahrscheinlichkeit für folgende Ereignisse:
A: Eine Apfelsine ist verdorben.
B: Alle Apfelsinen sind in Ordnung.
C:Mindestens zwei Apfelsinen sind verdorben.
4. Ausführliche Lösungen
Es handelt sich um einen n = 5-stufigen Bernoulliversuch mit der Erfolgswahrscheinlichkeit p = 1/5 = 0,2.
Rechneraufruf:[MENU] 1 [OPTN] {STAT} {DIST} {BINOMIAL} {Bpd} bzw. {Bcd}
Siehe auch Intervallwahrscheinlichkeit
A: Eine Apfelsine ist verdorben bedeutet: P(A) = P(X = 1)
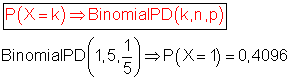
Die Wahrscheinlichkeit dafür, dass genau eine Apfelsine verdorben ist, ist 0,4096.
B: Alle Apfelsinen sind in Ordnung bedeutet: P(B) = P(X =0)
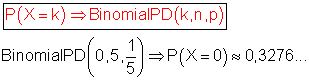
Die Wahrscheinlichkeit dafür, dass alle Apfelsinen in Ordnung sind, ist etwa 0,3276…
C: Mindestens zwei Apfelsinen sind verdorben bedeutet: P(C) = P(X ≥ 2)

Die Wahrscheinlichkeit dafür, dass mindestens zwei Apfelsinen verdorben sind, ist etwa 0,2627…
5.
Die Wahrscheinlichkeit für die Geburt eines Mädchens beträgt 0,49, für die Geburt eines Jungen 0,51. Wie groß ist die Wahrscheinlichkeit, dass in einer Familie mit 4 Kindern
A: genau zwei Mädchen sind?
B: höchstens 3 Mädchen sind?
5. Ausführliche Lösungen
Es handelt sich um einen n = 4-stufigen Bernoulliversuch mit der Erfolgswahrscheinlichkeit p = 0,49 (Mädchen).
Rechneraufruf:[MENU] 1 [OPTN] {STAT} {DIST} {BINOMIAL} {Bpd} bzw. {Bcd}
Siehe auch Intervallwahrscheinlichkeit
A: genau zwei Mädchen bedeutet: P(A) = P(X = 2)
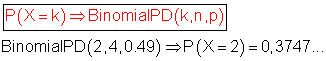
Die Wahrscheinlichkeit dafür, dass in der Familie genau zwei Mädchen sind, ist etwa 0,3747…
B: höchstens 3 Mädchen bedeutet: P(B) = P(X ≤ 3)
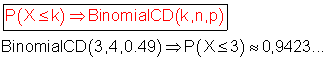
Die Wahrscheinlichkeit dafür, dass in der Familie höchstens drei Mädchen sind, ist etwa 0,9423…
6.
Wie oft muss man eine Münze mindestens werfen, um mit einer Wahrscheinlichkeit von mindestens 99% mindestens einmal Kopf zu erhalten?
6. Ausführliche Lösung
Die Wahrscheinlichkeit für Kopf und Zahl sei gleich ( p = 0,5).Das Gegenereignis von mindestens einmal Kopf ist keinmal Zahl.
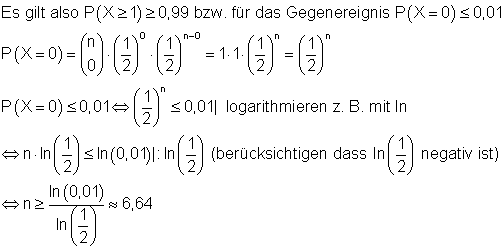
Die Münze muss mindestens 7 mal geworfen werden, um mit einer Sicherheit von mindestens 99% mindestens einmal Kopf zu erhalten.
Ergebniskontrolle:
Es handelt sich um einen n = 7-stufigen Bernoulliversuch mit der Erfolgswahrscheinlichkeit p = 0,5.
Zu überprüfen ist, ob P(X ≥ 1) ≥ 0,99 ist.
Rechneraufruf:
[MENU] 1 [OPTN] {STAT} {DIST} {BINOMIAL} {Bcd}
Siehe auch Intervallwahrscheinlichkeit
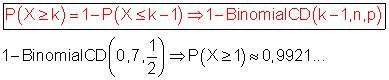
7.
Wie oft muss man mindestens Würfeln, um mit einer Wahrscheinlichkeit von mindestens 90% mindestens eine Sechs zu bekommen?
7. Ausführliche Lösung
Mindestens eine 6 bei n Würfen. E = { 1; 2 ; 3 ; … n } p = 1/6.
Das Gegenereignis von A lautet: Keine 6 bei n Würfen.
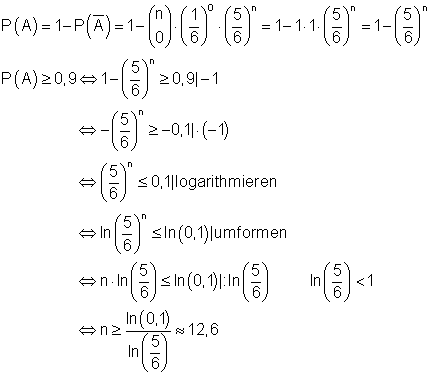
Man muss mindestens 13 mal würfeln, um mit einer Wahrscheinlichkeit von mindestens 90% mindestens eine 6 zu werfen.
Ergebniskontrolle:
Es handelt sich um einen n = 13-stufigen Bernoulliversuch mit der Erfolgswahrscheinlichkeit p = 1/6.
Zu überprüfen ist, ob P(X ≥ 1) ≥ 0,90 ist.
Rechneraufruf:
[MENU] 1 [OPTN] {STAT} {DIST} {BINOMIAL} {Bcd}
Siehe auch Intervallwahrscheinlichkeit
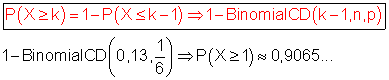
8.
Ein Würfel wird 60 mal geworfen.
Wie groß ist die Wahrscheinlichkeit für folgende Ereignisse:
A: Man wirft genau 10 mal die 6.
B: Man wirft mindestens 10 mal die 6.
C: Man wirft höchstens 10 mal die 6.
D: Die Anzahl der geworfenen Sechser liegt zwischen 6 und 12 einschließlich.
E: Man wirft mehr als 4 und weniger als 15 Sechser.
F: Die Augenzahl ist in weniger als 25 Fällen ungerade.
G: Die Augenzahl ist in mehr als 30 Fällen gerade.
H: Es treten mehr als 25 und weniger als 35 ungerade Augenzahlen auf.
8. Ausführliche Lösungen
Es handelt sich um einen n = 60-stufigen Bernoulliversuch mit der Erfolgswahrscheinlichkeit p = 1/6
Rechneraufruf:[MENU] 1 [OPTN] {STAT} {DIST} {BINOMIAL} {Bpd} bzw. {Bcd}
Siehe auch Intervallwahrscheinlichkeit
A: Man wirft genau 10 mal die 6 bedeutet: P(A) = P(X = 10)

Ist die Wahrscheinlichkeit dafür, genau 10 mal die 6 zu würfeln.
B: Man wirft mindestens 10 mal die 6 bedeutet: P(B) = P(X ≥ 10)
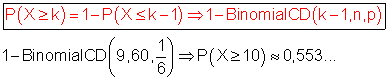
Ist die Wahrscheinlichkeit dafür, mindestens 10 mal die 6 zu werfen.
C: Man wirft höchstens 10 mal die 6 bedeutet: P(B) = P(X ≤ 10)
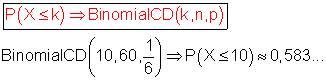
Ist die Wahrscheinlichkeit dafür, höchstens 10 mal die 6 zu werfen.
D: Die Anzahl der geworfenen Sechser liegt zwischen 6 und 12 einschließlich.
P(D) = P( 6 ≤ X ≤ 12)
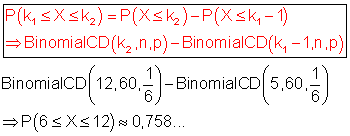
Ist die Wahrscheinlichkeit dafür, dass die Anzahl der Sechser zwischen 6 und 12 liegt.
E: Man wirft mehr als 4 und weniger als 15 Sechser bedeutet: P(E) = P( 5 ≤ X ≤ 14)
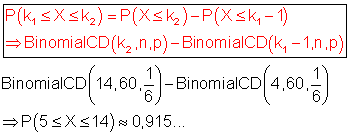
Ist die Wahrscheinlichkeit dafür, dass man mehr als 4 und weniger als 15 Sechser wirft.
F: Die Augenzahl ist in weniger als 25 Fällen ungerade bedeutet: P(F) = P( X ≤ 24) Achtung: p = 1/2
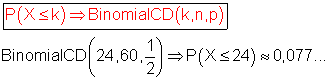
Ist die Wahrscheinlichkeit dafür, dass die Augenzahl in weniger als 25 Fällen ungerade ist.
G: Die Augenzahl ist in mehr als 30 Fällen gerade bedeutet: P(G) = P(X ≥ 31) Achtung: p = 1/2
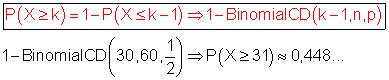
Ist die Wahrscheinlichkeit dafür, dass die Augenzahl in mehr als 30 Fällen gerade ist.
H: Es treten mehr als 25 und weniger als 35 ungerade Augenzahlen auf.P(H) = P( 26 ≤ X ≤ 34) Achtung: p = 1/2
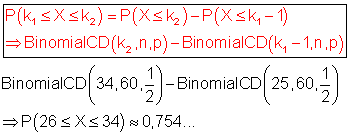
Ist die Wahrscheinlichkeit dafür, dass mehr als 25 und weniger als 35 mal ungerade Augenzahlen auftreten.
Rechenhelfer für die Binomialverteilung
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

