In diesem Beitrag definiere ich zuerst den Begriff Bernoulli-Experiment. Danach erkläre ich dies anhand eines Beispiels. Anschließend zeige ich, wie man die Anzahl der Pfade mit k Erfolgen und die Wahrscheinlichkeit für einen Pfad mit k Erfolgen aufstellt. Darauf folgt die Formel für die Pfadwahrscheinlichkeit. Daraus leite ich den Binomische Lehrsatz und die Definition der Binomialverteilung ab. Danach stelle ich zwei Übungen zur Verfügung. Anschließend erkläre ich die kumulierte Binomialverteilung. Dann stelle ich einen interaktiven Rechenhelfer für die Binomialverteilung und eine dritte Übung zur Verfügung. Zuletzt verlinke ich zu Aufgaben hierzu.
- Definition Bernoulli-Experiment.
- Beispiel
- Wahrscheinlichkeit für einen Pfad mit k Erfolgen
- Formel für die Pfadwahrscheinlichkeit.
- Binomischer Lehrsatz, Definition der Binomialverteilung ab.
- Übungen
- Kumulierte Binomialverteilung.
- Interaktiver Rechenhelfer für die Binomialverteilung
- Links zu Aufgaben
In den letzten Beiträgen zur Wahrscheinlichkeitsrechnung habe ich erklärt, wie man z. B. bei Glücksspielen Aussagen über den zu erwartenden Gewinn bzw. Verlust machen. Außerdem habe ich in Kombinatorik erklärt, wie man die Wahrscheinlichkeit für Ereignissen berechnet, die in einer bestimmten Reihenfolge, also in einer bestimmten Kombination, erfolgen.
Definition Bernoulli-Experiment
Viele Zufallsexperimente können als Experimente mit zwei Ergebnissen interpretiert werden, wie z.B.
- Münzwurf mit den Ergebnissen Wappen und Zahl
- Wurf einer Heftzwecke mit den Ergebnissen Rücken oder Spitze
- Werfen eines Würfels mit den Ergebnissen 6 oder keine 6.
Solche Experimente heißen Bernoulli-Experimente. Die beiden Ergebnisse eines solchen Experiments bezeichnet man als Erfolg oder als Misserfolg. Führt man einen solchen Versuch n-mal durch, dann spricht man von einem n-stufigen Bernoulli-Versuch oder einer Bernoulli-Kette der Länge n. Bei n-stufigen Bernoulli-Versuchen wird jedoch verlangt, dass das Ergebnis eines Einzelversuchs nicht durch die anderen Versuche beeinflusst wird. Man interessiert sich bei einem solchen n-stufigen Versuch nämlich für die Anzahl der Erfolge oder der Misserfolge.
Einführungsbeispiel zu Bernoulli
Wir werfen einen Würfel dreimal nacheinander. Wir interessieren uns dabei für die Wahrscheinlichkeit, mit der die Zahl 6 bei diesem Versuch 0, 1, 2 oder 3 mal auftritt.
E bedeutet dabei Erfolg oder Treffer, M bedeutet Misserfolg oder kein Treffer.
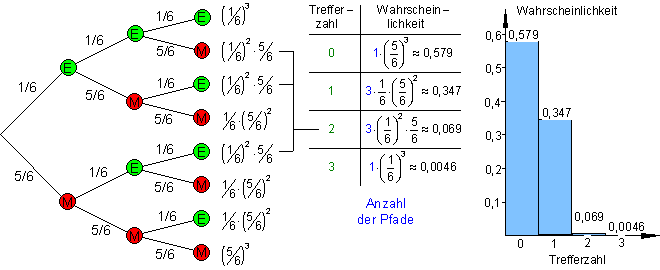
Hier handelt es sich also um einen dreistufigen Bernoulli-Versuch.
Aus dem Baumdiagramm lassen sich danach mittels der Pfadregeln leicht die Wahrscheinlichkeiten berechnen.
S = {EEE; EEM; EME; EMM; MEE; MEM; MME; MMM}.
Die Ergebnismenge enthält 8 Elemente (Anzahl der Pfade), die jeweils aus einer Anordnung von 3 Folgeereignissen besteht. Bei Erhöhung der Stufenzahl, ist die Bearbeitung der Aufgabe mit dem Baumdiagramm kaum mehr möglich.
Anzahl der Pfade mit k Erfolgen bei Bernoulli
Bei einem n-stufigen Bernoulli-Versuch besteht jedes Element der Ergebnismenge aus n Folgeereignissen z. B. EEMMEEEM …….EM. Die Anzahl der Pfade mit k Erfolgen zu finden ist gleichbedeutend damit, aus der Ergebnismenge die Anzahl der Elemente zu finden, die k-mal unabhängig von der Reihenfolge einen Erfolg aufweisen.
Anders ausgedrückt: Auf wie viele Arten kann man k Objekte aus n Objekten unabhängig von der Reihenfolge auswählen?
Das erinnert an dass Lotto-Problem, bei dem aus n = 49 Objekten k = 6 Objekte unabhängig von der Anordnung ausgewählt werden.
Die Anzahl der Möglichkeiten war dabei:
![]()
Diese Rechenvorschrift kann man auch auf den Bernoulli-Versuch übertragen, wenn wir dabei die Anzahl der Pfade mit k Erfolgen suchen.
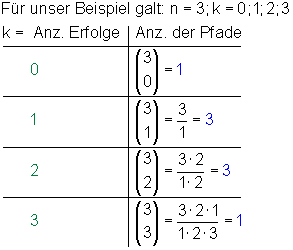
Die Anzahl der Pfade mit k Erfolgen bei einem n-stufigen Bernoulli-Versuch ist:
![]()
Beispiel
Ein Würfel wird n = 5 mal geworfen.
Als Erfolg werten wir dabei die Augenzahl 6.
Wie viel Pfade mit k = 3 Erfolgen gibt es im Ergebnisbaum?
![]()
Es gibt bei diesem Versuch also insgesamt 10 Pfade, die jeweils 3 Erfolge beinhalten.
Wahrscheinlichkeit für einen Pfad mit k Erfolgen
An einem konkreten Beispiel zeige ich jetzt die Rechenvorschrift zur Berechnung der Wahrscheinlichkeit eines Pfades. Diese Vorschrift ist dann zu verallgemeinern.
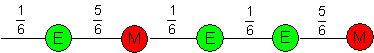
Die Wahrscheinlichkeit dieses Pfades kann man mit der Pfadmultiplikationsregel bestimmen:
![]()
Die Anzahl der Stufen für dieses Zufallsexperiment ist n = 5.
Dabei ist k = 3 die Anzahl der Erfolge.
Die Anzahl der Misserfolge ist folglich n – k = 5 – 3 = 2.
Diese Zahlen treten als Exponenten der Wahrscheinlichkeiten für einen Erfolg (p = 1/6) bzw. für einen Misserfolg (q = 5/6) auf.
Es gilt also q = 1 – p = 1 – 1/6 = 5/6.
Damit lässt sich die Wahrscheinlichkeit für bei n = 5 und k = 3 wie folgt berechnen:
![]()
Formel für die Pfadwahrscheinlichkeit:
Da es sich bei einem n-stufigen Bernoulli-Versuch um einen Versuch handelt, bei dem in jeder Stufe die Erfolgswahrscheinlichkeit P(E) = p gleich bleibt, gilt nach der Pfadmultiplikationsregel für jeden Pfad mit k Erfolgen und n – k Misserfolgen:
![]()
Wahrscheinlichkeit für k Erfolge bei einem n-stufigen Bernoulli-Versuch:

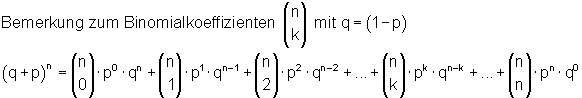
Das ist der Binomische Lehrsatz
Für das Einführungsbeispiel mit n = 3 gilt:
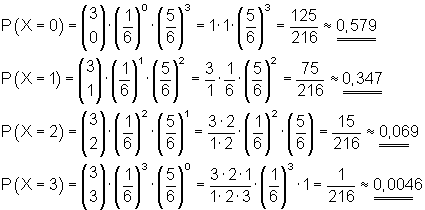
Definition Binomialverteilung:

Übung 1:
Eine Familie hat 6 Kinder.
Die Wahrscheinlichkeit ein Mädchen zu gebären beträgt dabei p = 0,5.
Berechnen Sie die Wahrscheinlichkeit dafür, das unter den 6 Kindern 0, 1, 2, 3, 4, 5, 6 Mädchen sind und zeichnen Sie das Histogramm der Wahrscheinlichkeitsverteilung. Bestimmen Sie danach die Wahrscheinlichkeit folgender Ereignisse:
A: Genau die Hälfte der Kinder sind Mädchen.
B: Höchstens die Hälfte der Kinder sind Mädchen.
C: Mindestens die Hälfte der Kinder sind Mädchen.
Lösung unten
Übung 2:
Wir werden eine Münze 5 mal und p sei 0,5.
a) Bestimmen Sie die Wahrscheinlichkeitsverteilung der Zufallsvariablen X: Anzahl der Wappen.
b) Mit welcher Wahrscheinlichkeit wirft man dabei
(1) Höchstens 3 mal Wappen
(2) Weniger als 3 mal Wappen
(3) mindestens 1 mal Wappen
(4) mehr als einmal Wappen?
Lösung unten
Kumulierte Binomialverteilung
Beispiel
Eine Münze wird 20 mal geworfen. Zu bestimmen sind die Wahrscheinlichkeiten für die Ereignisse:
a) Genau 10 mal Wappen.
b) Höchstens 15 mal Wappen.
c) Mindestens 7 mal Wappen.
d) Mindestens 6 mal und höchstens 16 mal Wappen.
Die Daten der Wahrscheinlichkeitsverteilung sind in folgender Tabelle zusammengestellt.
Dabei sind die Werte auf 3 Stellen nach dem Komma gerundet.
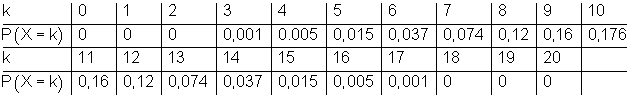
Bemerkung:
Für die Fälle k = 0, 1, 2 und 18, 19, 20 ist die Wahrscheinlichkeit dabei natürlich nicht Null. Die Null entsteht dadurch, dass auf drei Stellen nach den Komma gerundet wurde.
Das Histogramm einer solchen Binomialverteilung sieht wie folgt aus:
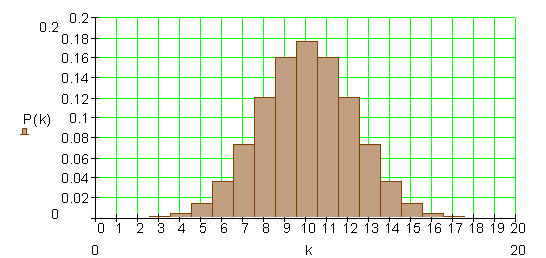
a) Die Wahrscheinlichkeit P( X = 10 ) kann man aus der Tabelle, bzw. aus dem Histogramm ablesen.
![]()
b) Die Wahrscheinlichkeit für das Ereignis
E: Höchstens 15 mal Wappen, kann man jedoch nicht unmittelbar ablesen. Dazu müssen die Tabellenwerte der Wahrscheinlichkeiten aufaddiert werden.
P( X = 0 ) + P( X = 1 ) + … + P( X = 15)
Hat man jedoch eine Tabelle in der die Wahrscheinlichkeiten bereits aufaddiert wurden, also eine kumulierte Tabelle, dann kann man die Wahrscheinlichkeit für E daraus sofort ablesen.
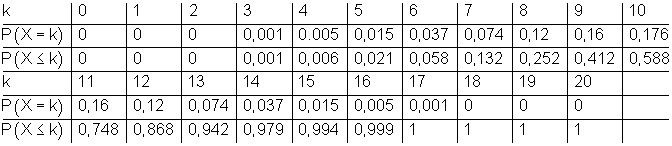
Bemerkung:
Für k < 3 ist die kumulierte Wahrscheinlichkeit dabei natürlich nicht Null. Ebenso sind die Werte für k < 20 auch nicht 1. Sie unterscheiden sich aber kaum noch von diesen Werten, so dass man in den meisten Fällen für praktische Berechnungen die gerundeten Tabellenwerte verwenden kann.Histogramm der kumulierten Binomialverteilung.
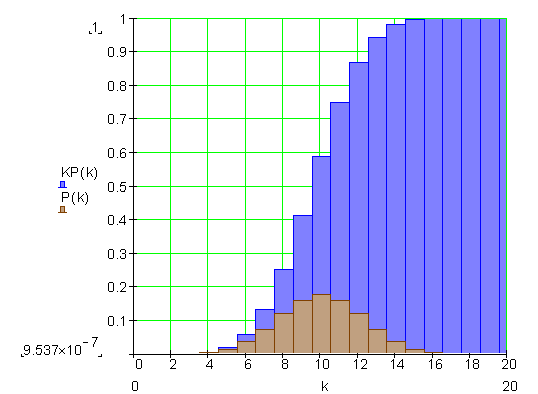
![]()
c) Mindestens 7 mal bedeutet:
![]()
d) Mindestens 6 mal und höchstens 16 mal bedeutet:
![]()
Das Beispiel zeigt, welchen Vorteil kumulierte Tabellen haben, wenn es darum geht, die Wahrscheinlichkeit für einen Bereich der Zufallsvariablen X zu berechnen. Diese Bereiche sind dann auf dem Zahlenstrahl auch als Intervalle darstellbar.
Wir unterscheiden folgende Fälle:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Übung 3:
a) Mehr als 20 Aufgaben
b) Mindestens 10 und höchstens 20 Aufgaben
c) Weniger als 10 Aufgaben
d) Genau 15 Aufgaben
Die Trefferwahrscheinlichkeit pro Aufgabe ist 1/5 = 0,2. Da diese Wahrscheinlichkeit bei jeder der 50 Aufgaben besteht, kann der Vorgang als 50 stufiger Bernoulli- Versuch betrachtet werden. Der Auszug aus der kumulierten Binomialverteilung mit n = 50 und p = 0,2 soll als Hilfestellung genutzt werden.
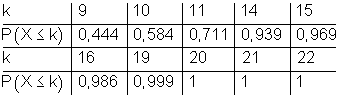
Lösung unten
Lösungen der Übungen:
Übung 1:
Eine Familie hat 6 Kinder.
Die Wahrscheinlichkeit ein Mädchen zu gebären betrage p = 0,5.
Berechnen Sie die Wahrscheinlichkeit dafür, das unter den 6 Kindern 0, 1, 2, 3, 4, 5, 6 Mädchen sind und zeichnen Sie das Histogramm der Wahrscheinlichkeitsverteilung. Bestimmen Sie die Wahrscheinlichkeit folgender Ereignisse:
A: Genau die Hälfte der Kinder sind Mädchen.
B: Höchstens die Hälfte der Kinder sind Mädchen.
C: Mindestens die Hälfte der Kinder sind Mädchen.
Lösung: Das Problem kann als 6- stufiger Bernoulli- Versuch betrachtet werden mit n = 6 und p = 0,5.
Gesucht ist P( X = k ) für k = 0, 1, 2, 3, 4, 5, 6
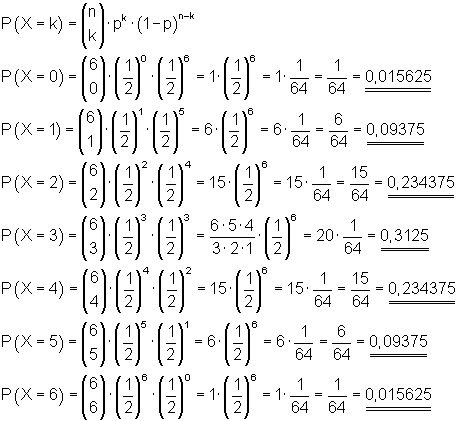
Histogramm der Wahrscheinlichkeitsverteilung:
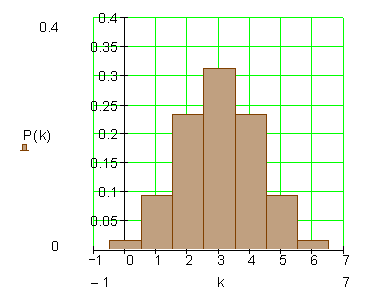

Übung 2:
Eine Münze wird 5 mal geworfen und p sei 0,5.
a) Bestimmen Sie die Wahrscheinlichkeitsverteilung der Zufallsvariablen X: Anzahl der Wappen.
b) Mit welcher Wahrscheinlichkeit wirft man
(1) Höchstens 3 mal Wappen
(2) Weniger als 3 mal Wappen
(3) mindestens 1 mal Wappen
(4) mehr als einmal Wappen?
Lösung: Das Problem kann als 5- stufiger Bernoulli- Versuch betrachtet werden mit n = 5 und p = 0,5.
a) Gesucht ist P( X = k ) für k = 0, 1, 2, 3, 4, 5
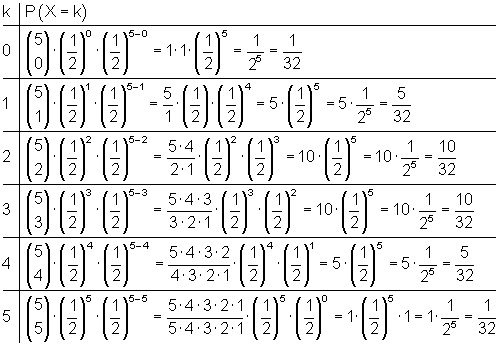
b) (1) Höchstens 3 mal Wappen bedeutet dabei:
![]()
(2) Weniger als 3 mal Wappen bedeutet dabei:
![]()
(3) Mindestens 1 mal Wappen bedeutet dabei:
![]()
(4) Mehr als 1 mal Wappen bedeutet dabei:
![]()
Übung 3:
Ein Multiple- Choice- Test besteht aus 50 Aufgaben mit jeweils 5 Antworten, von denen nur jeweils eine richtig ist. Mit welcher Wahrscheinlichkeit kann man durch bloßes Raten folgende Anzahl von Aufgaben richtig beantworten?
a) Mehr als 20 Aufgaben
b) Mindestens 10 und höchstens 20 Aufgaben
c) Weniger als 10 Aufgaben
d) Genau 15 Aufgaben
Die Trefferwahrscheinlichkeit pro Aufgabe ist 1/5 = 0,2. Da diese Wahrscheinlichkeit bei jeder der 50 Aufgaben besteht, kann der Vorgang als 50 stufiger Bernoulli-Versuch betrachtet werden. Der Auszug aus der kumulierten Binomialverteilung mit n = 50 und p = 0,2 soll dabei als Hilfestellung genutzt werden.
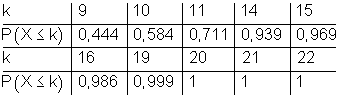
Lösung: a)
![]()
Die Wahrscheinlichkeit durch bloßes Raten mehr als 20 Aufgaben richtig zu beantworten ist folglich kleiner als 0,001 (0,1%).
b)
![]()
Die Wahrscheinlichkeit durch bloßes Raten mindestens 10 und höchstens 20 Aufgaben richtig zu beantworten ist folglich 0,565 (56,5%).
c)
![]()
Die Wahrscheinlichkeit durch bloßes Raten weniger als 10 Aufgaben richtig zu beantworten ist folglich 0,444 (44,4%).
d)
![]()
Die Wahrscheinlichkeit durch bloßes Raten genau 15 Aufgaben richtig zu beantworten ist folglich 0,03 (3%).


