Zufallsvariable, Wahrscheinlichkeitsverteilungen, Erwartungswert

Einführungsbeispiel

Wir werfen einen blauer und einen grünen Würfel zusammen 400 mal. Danach notieren wir die Häufigkeiten der einzelnen Ergebnisse  in einer Tabelle. Jedem der Zahlenpaare ( 1 | 1) … ( 6 | 6) ordnen wir dabei deren Augensumme zu.

Anschließend vergleichen wir die relativen Häufigkeiten der Augensummen mit der Wahrscheinlichkeit ihres Auftretens. Dazu stellen wir die Ergebnisse in einer Tabelle und in einem Säulendiagramm dar.

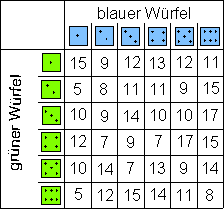
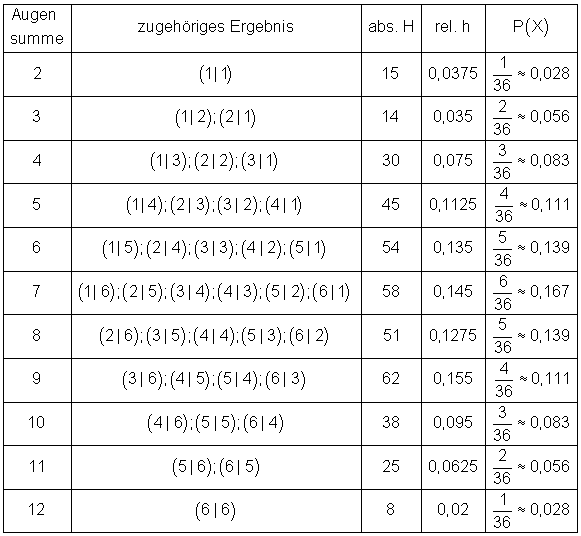
Tabelle:

Säulendiagramm:

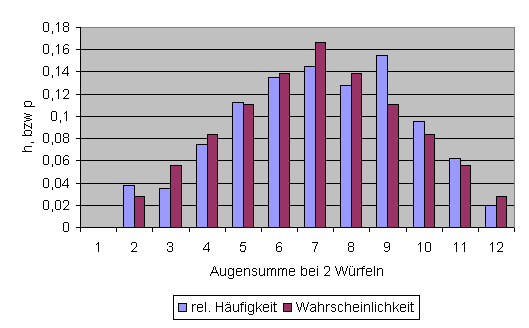
Die relativen Häufigkeiten für die einzelnen Augensummen weichen also nicht stark von den berechneten Wahrscheinlichkeiten ab. Voraussetzung ist dabei natürlich eine hohe Anzahl von Versuchen.

Zufallsvariable

Defintion Zufallsvariable:

Dazu die Wertetabelle einer Zufallsvariablen für den Wurf zweier Würfel, deren Augenzahl wir addiert haben:

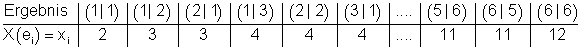
Wahrscheinlichkeitsverteilung

Wenn wir beim Werfen mit zwei Würfeln jedem Ergebnis die Augensumme zuordnen, entsteht die Zufallsvariable X.
Ordnet man dann jedem Wert dieser Zufallsvariablen ihre Wahrscheinlichkeit zu, entsteht eine Wahrscheinlichkeitsverteilung. Mit anderen Worten eine Wahrscheinlichkeitsfunktion. Die Wahrscheinlichkeitsverteilung oder Verteilung der Zufallsgröße kann man mit einer Tabelle und einem Histogramm darstellen.

Tabelle:

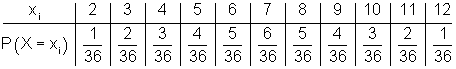
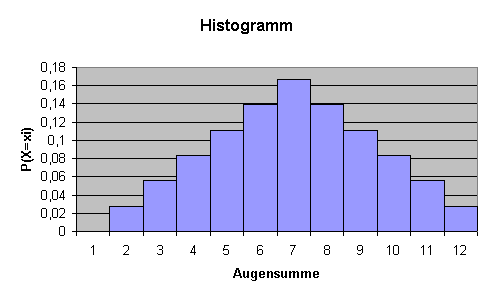
Definition Wahrscheinlichkeitsverteilung

Funktionsdarstellung zum Beispiel werfen zweier Würfel, deren Augensumme gebildet wird.

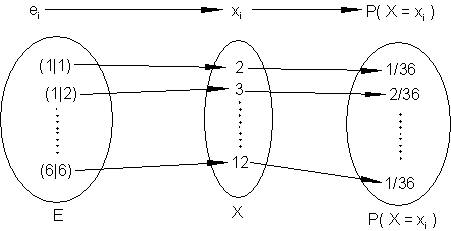
Erwartungswert einer Wahrscheinlichkeitsverteilung

Mit Hilfe der Wahrscheinlichkeit möchte man z. B. bei Glücksspielen Aussagen über den zu erwartenden Gewinn bzw. Verlust machen. Dabei stellt sich die Frage: Welchen Gewinn pro Spiel kann man bei häufiger Durchführung erwarten?

Beispiel:

Dazu betrachten wir wieder die Augensumme der zwei Würfel. Man könnte ein Glücksspiel daraus machen, indem man folgende Regel aufstellt:

Regel:

Die in einem Wurf erreichte Augensumme wird in € ausgezahlt.

Der Betreiber des Spiels muss sich natürlich Gedanken darüber machen, wie hoch der Einsatz pro Spiel sein muss, damit er keinen Verlust erleidet. Dazu muss er wissen, welchen Betrag er im Mittel pro Spiel bei sehr vielen Spielen auszuzahlen hat. So hoch muss auch mindestens der Einsatz ein.

Ähnlich wie bei der Mittelwertbildung aus einer Häufigkeitsverteilung in der beschreibenden Statistik kann man durch Multiplikation der Auszahlungsbeträge mit ihren Wahrscheinlichkeiten einen Wert bilden.

Diesen Wert nennen wir Erwartungswert.

Für unser Beispiel bedeutet der Wert 7, dass bei einer hohen Anzahl von Spielen im Mittel 7 € pro Spiel auszuzahlen sind.

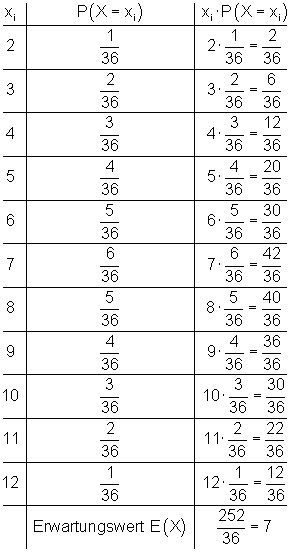
Der Betreiber des Spiels muss also mindestens einen Einsatz von 7 € pro Spiel verlangen, damit er keinen Verlust erleidet.
Die Auszahlungsbeträge oder auch Ausspielungen entsprechen der Zufallsvariablen
X mit den Werten: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.

Nun betrachten wir das Spiel aus der Sicht eines Spielers, der pro Spiel 7 € Einsatz zahlen muss.
Für ihn berechnet sich der Gewinn aus:
Gewinn = Ausspielung – Einsatz.
Der Gewinn entspricht nun einer Zufallsvariablen, die wir Y nennen, also Y mit den Werten: -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5.
Damit lässt sich nun der Erwartungswert für den Gewinn ermitteln.

Der Erwartungswert für einen Gewinn ist also 0. Mit anderen Worten, auf lange Sicht gewinnt der Spieler nichts. Aber er verliert auch nichts. Die Chancen sind somit ausgeglichen.

Formel: Erwartungswert von X

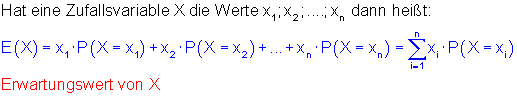
Wann ist ein Spiel fair:

Ist E(X)

• > 0, dann nennt man das Spiel günstig für den Spieler.
• = 0, dann nennt man das Spiel fair.
• < 0, dann nennt man das Spiel ungünstig (unfair) für den Spieler.

Bemerkungen zum Erwartungswert:

Der Erwartungswert ist der zu erwartende Mittelwert von X in einer Reihe von Zufallsversuchen.
Der Mittelwert aus der beschreibenden Statistik bezieht sich auf die Vergangenheit. Also auf Werte, die in einer Stichprobe tatsächlich aufgetreten sind.

Der Erwartungswert in der Wahrscheinlichkeitsrechnung dagegen bezieht sich auf die Zukunft. Also auf eine Größe, mit der auf lange Sicht zu rechnen ist.

Der Erwartungswert betrug oben E(X) = 0. Aber diesen Wert kann die Zufallsvariable X nicht einnehmen. Ähnlich ist es ja auch beim Mittelwert.

Beispiel und Übungen

Trotz Verbotes spielen Schüler auf dem Schulhof ein Glücksspiel.
Die Spielregeln dabei:
Der Einsatz pro Spiel beträgt 2 €.
Der Spieler setzt zuerst eine der Zahlen 1, 2, 3, … , 6.
Anschließend wirft er dreimal mit einem Würfel.
Fällt die gesetzte Zahl

• nicht, ist der Einsatz verloren.
• einmal, dann erhält er seinen Einsatz zurück.
• zweimal, dann erhält er den doppelten Einsatz.
• dreimal, dann erhält er den dreifachen Einsatz.

Wie groß sind die Gewinnaussichten?
Die Zufallsvariable X ist dabei der Nettogewinn. Das ist der an den Spieler auszuzahlende Betrag abzüglich des Einsatzes von 2 €. Wenn der Spieler verloren hat, also 0 – 2 = -2. Wenn er dreimal die gesetzte Zahl wirft, 6 – 2 = 4.

Mit Hilfe des dreistufigen Baumdiagramms und der Pfadregel errechnet man die Wahrscheinlichkeit für einen Gewinn bzw. einen Verlust.
Es gilt: G = Gewinn, V = Verlust.

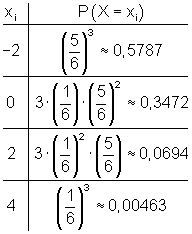
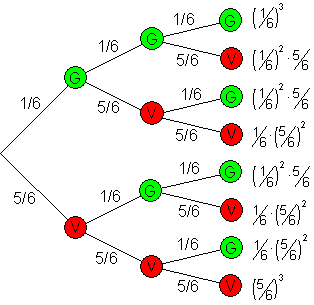
Zur Berechnung der Gewinnaussichten multipliziert man die Werte der Zufallsvariablen mit ihren zugehörigen Wahrscheinlichkeiten und addiert die Ergebnisse:

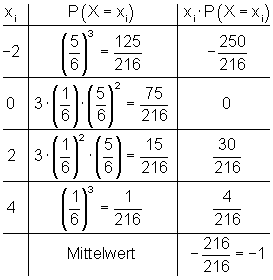
Die errechnete Zahl von -1 sagt aus, dass der Spieler bei vielen Wiederholungen einen Verlust von 1 Euro pro Spiel erwarten muss.
Diesen Betrag kassiert natürlich die Bank. Langfristig sind Gewinn und Verlust nicht ausgeglichen. Deshalb bezeichnet man das Spiel als unfair.
Gewinn und Verlust wären bei einem Mittelwert von 0 ausgeglichen. Das wäre dann ein faires Spiel. Das könnte man z.B. durch eine Gewinnerhöhung erreichen.

Übung 1:

Der Erwartungswert, bei dem oben vorgestellten Würfelspiel war E(X) = -1.
Das Spiel ist also unfair.
Wie hoch müsste der Einsatz für ein Spiel sein, damit man das Spiel als fair bezeichnen könnte?
Die Auszahlungen bleiben vom Betrag her gleich:
Fällt die gesetzte Zahl

• nicht, ist die Auszahlung 0 €.
• einmal, dann ist die Auszahlung 2 €.
• zweimal, dann ist die Auszahlung 4 €.
• dreimal, dann ist die Auszahlung 6 €.

Die Lösung dazu ist unten.

Übung 2:

Jedes Los gewinnt ! Bei der Abi-Abschlussfeier muss jeder der 50 Teilnehmer ein Los kaufen. Der 1. Preis hat einen Wert von 100 €, der 2. von 25 € und der 3. von 10 €. Jeder, der keinen dieser Gewinne bekommt, erhält einen Trostpreis in Höhe von 1 €.
a) Wie teuer müsste ein Los sein, damit Einnahmen und Ausgaben überein stimmen?
b) Jedes Los wird für 5 € verkauft. Der Erlös geht ans Friedensdorf. Wie groß ist der Erlös?
Die Lösung dazu findest du unten.

Übung 3:

Eine Urne enthält eine rote, eine schwarze und eine grüne Kugel.
Es wird solange ohne zurücklegen eine Kugel gezogen, bis eine grüne Kugel erscheint.
Wird die grüne Kugel im

• 1. Zug gezogen, dann ist die Ausspielung 2 €.
• 2. Zug gezogen, dann ist die Ausspielung 1 €.
• 3. Zug gezogen, dann ist die Ausspielung 0 €.

Wie hoch muss der Einsatz sein, damit es sich um ein faires Spiel handelt?
Die Lösung dazu ist unten.

Lösungen

Übung 1:

Der Erwartungswert, bei dem oben vorgestellten Würfelspiel war E(X) = -1.
Das Spiel ist also unfair.
Wie hoch müsste der Einsatz für ein Spiel sein, damit man das Spiel als fair bezeichnen könnte?
Die Auszahlungen bleiben vom Betrag her gleich:
Fällt die gesetzte Zahl

• nicht, ist die Auszahlung 0 €.
• einmal, so ist die Auszahlung 2 €.
• zweimal, so ist die Auszahlung 4 €. dreimal, so ist die Auszahlung 6 €.

Lösung:

Fair ist das Spiel dann, wenn auf lange Sicht genau soviel ausgespielt wird, wie eingenommen wird.
Dazu berechnen wir den Erwartungswert der Auszahlungen.
E(X) = 1 bedeutet, dass über lange Sicht im Mittel 1 € pro Spiel ausgezahlt wird.
Bei einem Einsatz von ebenfalls 1 € pro Spiel, ist das Spiel fair.

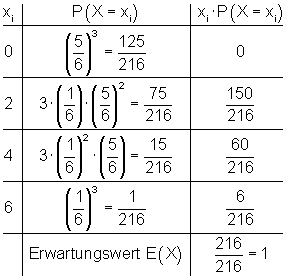
Übung 2: Jedes Los gewinnt!

Bei der Abi-Abschlussfeier muss jeder der 50 Teilnehmer ein Los kaufen.
Der 1. Preis hat einen Wert von 100 €, der 2. von 25 € und der 3. von 10 €.
Jeder, der keinen dieser Gewinne bekommt, erhält einen Trostpreis in Höhe von 1 €.
Wie teuer müsste ein Los sein, damit Einnahmen und Ausgaben überein stimmen?
Jedes Los wird für 5 € verkauft.
Der Erlös geht ans Friedensdorf. Wie groß ist der Erlös?
Lösung:
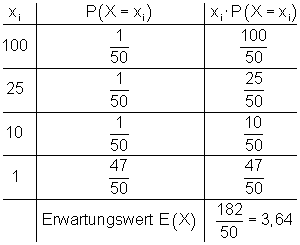
a) Der Erwartungswert wird berechnet:
E(X) = 3,64 bedeutet, dass jedes Los 3,65 € kosten muss, damit die Ausgaben gedeckt werden.
b) Bei einem Lospreis von 5 € und 50 verkauften Losen entsteht ein Gewinn von 50(5 – 3,64) = 68 €.
Dieser Betrag geht ans Friedensdorf.

Übung 3:

Eine Urne enthält eine rote, eine schwarze und eine grüne Kugel.
Es wird solange ohne zurücklegen eine Kugel gezogen, bis eine grüne Kugel erscheint.
Wird die grüne Kugel im
1. Zug gezogen, so ist die Ausspielung 2 €.
2. Zug gezogen, so ist die Ausspielung 1 €.
3. Zug gezogen, so ist die Ausspielung 0 €.
Wie hoch muss der Einsatz sein, damit es sich um ein faires Spiel handelt?
Lösung: Mit Hilfe des dreistufigen Baumdiagramms und der Pfadregel errechnet man die Wahrscheinlichkeiten dafür eine grüne Kugel zu ziehen.

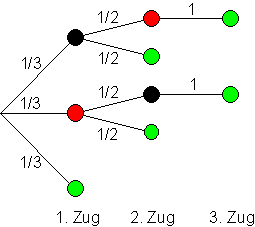
Der Erwartungswert der Ausspielung ist E(X) = 1.
Wenn es sich um ein faires Spiel handeln soll, muss der Einsatz ebenfalls 1 € betragen.

Im nächsten Beitrag geht es um Bernoulli-Versuche und die Binomialverteilung.