In diesem Beitrag zeige ich zuerst, wie man mit den grafikfähigen Taschenrechnern Casio fx-CG20 und Casio fx-CG50 die Intervallwahrscheinlichkeit bei einem n-stufiger Bernoulli-Versuch berechnet. Danach erkläre ich anhand eines Beispiels die Berechnung von Intervallgrenzen. Anschließend gebe ich eine Zusammenfassung über die Grenzen bei der Binomialverteilung. Zuletzt gehe ich auf Normalverteilung und Intervalle ein.
Casio fx-CG20 auf Casio fx-CG50 updaten
Intervallwahrscheinlichkeit
Ein n-stufiger Bernoulli-Versuch mit der Erfolgswahrscheinlichkeit p, wird durch eine Binomialverteilung dargestellt.
Mehr dazu siehe Bernoulli-Versuche und die Binomialverteilung.
Der Erwartungswert ist dabei die Anzahl der Erfolge mit der größten Wahrscheinlichkeit.
Wird Zum Beispiel ein Würfel n = 600 mal geworfen, so erwartet man k = 100 mal die Zahl 6.
Die Zahl 6 kann bei 600 Versuchen jedoch auch k = 0 mal oder k = 600 mal auftreten.
Die Wahrscheinlichkeiten dafür sind verschwindend gering.
Wenn ein Würfel wird n = 600 mal geworfen wird, zählt die Zahl 6 als Erfolg mit der Erfolgswahrscheinlichkeit p = 1/6.
Wie groß ist die Wahrscheinlichkeit dafür, dass bei den 600 Würfen genau k = 100 mal die 6 geworfen wird?
Wenn wir eingeben
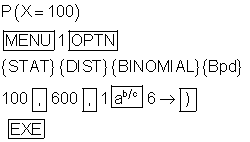
erscheint danach auf dem Display:
BinomialPD(100,600,1/6)
0.04366432132 .
Die Wahrscheinlichkeit dafür, dass bei 600 Würfen genau 100 mal die Zahl 6 geworfen wird,
beträgt etwa 0,043…
Allgemein gilt für [ 0 ====== ][ k ][ ====== n ]:
![]()
Dabei stellt k die Anzahl der Erfolge, n die Anzahl der Versuche und p die Erfolgswahrscheinlichkeit dar.
Wie groß ist die Wahrscheinlichkeit dafür, dass bei den 600 Würfen höchstens k = 100 mal die 6 geworfen wird?
Wenn wir eingeben
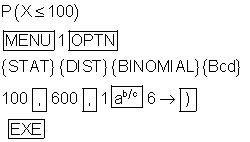
erscheint danach auf dem Display:
BinomialCD(100,600,1/6)
0.5266726941 .
Die Wahrscheinlichkeit dafür, dass bei 600 Würfen höchstens 100 mal die Zahl 6 geworfen wird,
beträgt etwa 0,526…
Allgemein gilt für [ 0 ====== k ][ ====== n ]:
![]()
Dabei stellt k die Anzahl der Erfolge, n die Anzahl der Versuche und p die Erfolgswahrscheinlichkeit dar.
Hierbei handelt es sich um die kumulierte Wahrscheinlichkeit.
Wie groß ist die Wahrscheinlichkeit dafür, dass bei den 600 Würfen mindestens k = 100 mal die 6 geworfen wird?
Wenn wir eingeben

Erscheint danach auf dem Display:
1 – BinomialCD(99,600,1/6)
0.5169916272
Die Wahrscheinlichkeit dafür, dass bei 600 Würfen mindestens 100 mal die Zahl 6 geworfen wird,
beträgt etwa 0,516…
Allgemein gilt für [ 0 ====== ][ k ====== n ]:
![]()
dabei ist k die Anzahl der Erfolge,
n die Anzahl der Versuche und p die Erfolgswahrscheinlichkeit darstellt.
Wie groß ist die Wahrscheinlichkeit dafür, dass bei den 600 Würfen die Anzahl der 6-er zwischen 90 und 110 (einschließlich) liegen?
Wenn wir eingeben

Erscheint danach auf dem Display:
BinomialCD(110,600,1/6) – BinomialCD(89,600,1/6)
0.7501249252
Die Wahrscheinlichkeit dafür, dass bei 600 Würfen die Anzahl der 6-er, zwischen 90 und 110 liegen,
beträgt etwa 0,750…
Allgemein gilt für [ 0 === ][ k1 === k2 ][ === n ]:
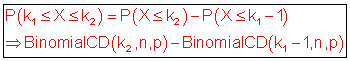
Dabei stellt k die Anzahl der Erfolge, n die Anzahl der Versuche und p die Erfolgswahrscheinlichkeit dar.
Intervallgrenzen werden berechnet
Statt der Wahrscheinlichkeit für die Anzahl der Erfolge eines Bernoulliversuchs in einem bestimmten Intervall,
kann man bei Vorgabe einer Intervallwahrscheinlichkeit die Intervallgrenzen k bestimmen.
Das benötigen wir bei Hypothesentests zur Bestimmung von Annahme- bzw. Ablehnungsbereich.
Die Wahrscheinlichkeit dafür, dass bei n= 600 Würfen eines Würfels höchstens k Erfolge auftreten soll höchstens α ≤ 5% betragen.
Das bedeutet, für welches k ist die Forderung erfüllt?
![]()
Wenn wir eingeben
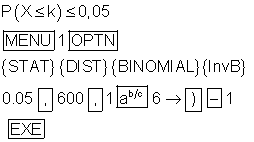
Erscheint danach auf dem Display:
InvBinomialCD(0.05,600,1/6) – 184
![]()
Der linke untere 5%-Bereich gilt für [ 0 … k … 84 ] oder
die Wahrscheinlichkeit dafür, das höchstens k = 84 Erfolge auftreten ist kleiner als 5%.
Allgemein gilt: (Linksseitiger Hypothesentest)

[ 0 === ≤ α === k ][ k + 1 === n ]
Das Ergebnis kann mit
![]()
überprüft werden. Hier ein Beispiel dafür.
Allgemein gilt:
Diese Rechnung ist für den linksseitigen Hypothesentest nötig.
Die Wahrscheinlichkeit dafür, dass bei n= 600 Würfen eines Würfels höchstens k Erfolge auftreten soll höchstens α ≤ 5% betragen.
Das bedeutet, für welches k ist die Forderung erfüllt?
![]()
Diese Bedingung ermöglicht es also die Anzahl der Erfolge zu finden, die sich in dem rechten oberen 5%-Bereich befinden.
Wenn wir eingeben
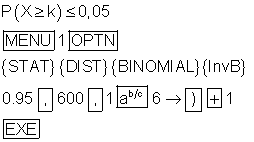
Erscheint danach auf dem Display:
InvBinomialCD(0.95,600,1/6) + 1
116
![]()
Allgemein gilt: (Rechtsseitiger Hypothesentest)

[ 0 === k – 1 ][ k === ≤ α === n ]
Das Ergebnis kann mit
![]()
überprüft werden. Beispiel
Diese Rechnung ist für den rechtsseitigen Hypothesentest nötig.
Bei n= 600 Würfen eines Würfels soll die Anzahl der Erfolge in einer symmetrischen 95%-Umgebung vom Erwartungswert liegen.
Wir bestimmen die Intervallgrenzen k1 und k2.
Das bedeutet, für welche Werte von k1 und k2 ist folgende Forderung erfüllt?
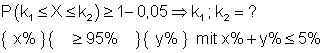
Wenn wir eingeben

Erscheint danach auf dem Display:
InvBinomialCD(0.025,600,1/6) – 1
81 = k1
![]()
Wenn wir eingeben

Erscheint danach auf dem Display:
InvBinomialCD(0.975,600,1/6) +1
119 = k2
![]()
![]()
Allgemein gilt: (Beidseitiger Hypothesentest)
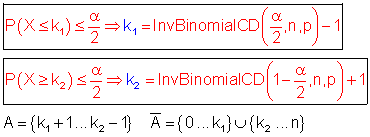
[ 0 === ≤ α/2 === k1 ][ k1 + 1====== k2 – 1 ][ k2 === ≤ α/2 === n ]
Das Ergebnis kann mit
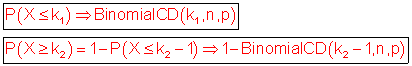
überprüft werden. Beispiel
Diese Rechnung ist für den beidseitigen Hypothesentest nötig.
Zusammenfassung Binomialverteilung
![]()
[ 0 ====== ][ k ][ ====== n ]
![]()
[ 0 ====== k ][ ====== n ]
![]()
[ 0 ====== ][ k ====== n ]
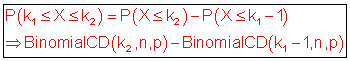
[ 0 === ][ k1 === k2 ][ === n ]
Linksseitiger Hypothesentest Ein Klick auf diesen Link führt zu Erklärungen dazu.

[ 0 === ≤ α === k ][ k + 1 === n ] Beispiel
Rechtsseitiger Hypothesentest Ein Klick auf diesen Link führt zu Erklärungen dazu.

[ 0 === k – 1 ][ k === ≤ α === n ] Beispiel
Beidseitiger Hypothesentest Ein Klick auf diesen Link führt zu Erklärungen dazu.
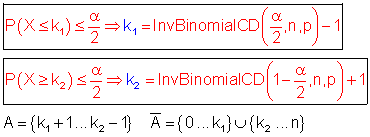
[ 0 === ≤ α/2 === k1 ][ k1 + 1====== k2 – 1 ][ k2 === ≤ α/2 === n ] Beispiel
Normalverteilung und Intervalle
Um mit der Normalverteilung zu rechnen, geht man ähnlich vor, wie bei der Binomialverteilung.
[MENU] 1 [OPTN] {STAT} {DIST} {NORM}
{Npd} berechnet einen einzelnen Wert.
{NcD} berechnet die kumulative Normalverteilung.
{InvN} ermittelt die Umkehrform der kumulativen Normalverteilung.
Es gilt:
μ : Erwartungswert der Zufallsvariablen k.
σ : Standardabweichung.
Falls die Standardabweichung größer 3 ist, kann man die Binomialverteilung durch die Normalverteilung hinreichend genau approximieren.
Bei Intervallberechnungen muss man folglich berücksichtigen, das die Binomialverteilung für diskrete Werte, die Normalverteilung aber für kontinuierliche Werte bestimmt ist.
![]()
[ 0 ====== ][ k ][ ====== n ]
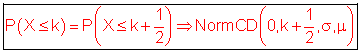
[ 0 ====== k ][ ====== n ]
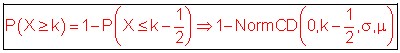
[ 0 ====== ][ k ====== n ]
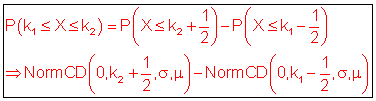
[ 0 === ][ k1 === k2 ][ === n ]
Linksseitiger Hypothesentest
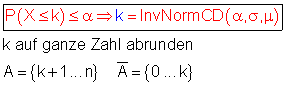
[ 0 === ≤ α === k ][ k + 1 === n ]
Rechtsseitiger Hypothesentest

[ 0 === k – 1 ][ k === ≤ α === n ]
Beidseitiger Hypothesentest

[ 0 === ≤ α/2 === k1 ][ k1 + 1====== k2 – 1 ][ k2 === ≤ α/2 === n ]
Beim beidseitigem Hypothesentest sollten die Grenzen des Ablehnungsbereichs also symmetrisch zum Erwartungswert sein.
Hier findest du eine Übersicht über alle Beiträge zum Thema Wahrscheinlichkeitsrechnung.
Weitere Beispiele zu dem Casio fx-CG20 findest du in der Kategorie GTR.
Außerdem in der Übersicht über alle Beiträge zum grafikfähigen Taschenrechner Casio fx-CG20.


