In diesem Beitrag führe ich anhand von leicht verständlichen Beispielen und Übungen in die Wahrscheinlichkeitsrechnung ein. Zuerst definiere ich die Begriffe Zufallsexperiment und einstufiges Zufallsexperiment. Danach erkläre ich Ergebnis und Ergebnismenge. Anschließend zeige ich die Darstellung in der Mengenschreibweise und als Baumdiagramm. Zuletzt erkläre ich das mehrstufige Zufallsexperiment.
Wenn es um Wahrscheinlichkeiten geht, denken wir zuerst an Würfel. Denn die Augenzahl hängt vom Zufall ab. Deshalb nennt man solche Versuche Zufallsexperimente.
Definition Zufallsexperimente in der Wahrscheinlichkeitsrechnung
Ein Zufallsexperiment ist also ein Experiment mit folgenden Eigenschaften:
- Unter gleichen Bedingungen beliebig oft wiederholbar
- Außerdem gibt es mindestens zwei mögliche Ergebnisse
- Das Ergebnis ist nicht vorhersagbar.
Beispiel für Zufallsexperimente:
Das Werfen eines Würfels ist eines, denn
- es ist beliebig oft wiederholbar,
- außerdem gibt es 6 mögliche Ergebnisse
- und das Ergebnis ist nicht vorhersagbar.
Übung 1:
Ist die Wette über den Ausgang eines Fußballspiels also ein Zufallsexperiment?
Die Lösung hierzu findest du unten.
Definition einstufige Zufallsexperimente
Wenn ein Zufallsexperiment einmal ausgeführt wird, spricht man von einem einstufigen Zufallsexperiment.
Beispiel:
- Einmaliges werfen eines Würfels,
- einer Münze,
- einmalige Wette über den Ausgang eines Fußballspiels.
Definition Ergebnis:
Der Ausgang des Zufallsexperimentes wird Ergebnis genannt.
Beispiele:
Wenn man einmal würfelt, kann das Ergebnis z. B. 4 sein.
Beim einmaligen Werfen einer Münze dagegen die Zahl.
Bei der einmalige Wette über den Ausgang eines Fußballspiels schließlich Sieg.
Definition Ergebnismenge in der Wahrscheinlichkeitsrechnung
Die Ergebnismenge enthält alle möglichen Ergebnisse eines Zufallsexperimentes.
Mit anderen Worten: Stichprobenraum, oder Ereignisraum oder Ergebnisraum.
Beispiele:
Wenn wir einmal würfeln, ist die Ergebnismenge: S = {1; 2; 3; 4; 5; 6}.
Beim einmaliges werfen einer Münze dagegen: Ergebnismenge: S = {Zahl; Wappen}.
Bei der einmalige Wette über den Ausgang eines Fußballspiels schließlich: Ergebnismenge: S = {Sieg; unentschieden; Niederlage}.
Übung 2:
Gib drei weitere Zufallsexperimente mit ihrer jeweiligen Ergebnismenge an!
Die Lösung hierzu ist unten.
Darstellung der Ergebnismenge eines Zufallsexperimentes in der Wahrscheinlichkeitsrechnung
Die Ergebnismenge kann in der Mengenschreibweise oder als Baumdiagramm dargestellt werden.
Wenn du wissen willst, wie man das erstellt, schaue dir das 📽️Video Baumdiagramm Ergebnismenge an.
| Darstellung in der Mengenschreibweise | Darstellung als Baumdiagramm |
| Einmaliges werfen eines Würfels | |
| Ergebnismenge: S = {1; 2; 3; 4; 5; 6} | 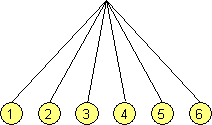 |
| Einmaliges werfen einer Münze | |
| Ergebnismenge: S = {Zahl; Wappen} | 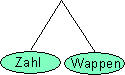 |
| Einmalige Wette über den Ausgang eines Fußballspiels | |
| Ergebnismenge: S = {Sieg; unentschieden; Niederlage} | 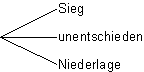 |
Zusammenhang Ergebnis und Ergebnismenge eines Zufallsexperimentes
Das Ergebnis e ist ein einzelner Ausgang von mehreren möglichen Ausgängen eines Zufallsexperiment.
Die Zusammenfassung aller möglichen Ergebnisse ist daher die Ergebnismenge.
Z. B. S = {e_1; e_2; ...; e_n} .
Mehrstufige Zufallsexperimente in der Wahrscheinlichkeitsrechnung
Zufallsexperimente, die sich aus mehreren hintereinander ausgeführten einstufigen Experimenten zusammensetzen, nennt man folglich mehrstufige Zufallsexperimente.
Beispiel:
Wenn man eine Heftzwecke einmal wirft, ist die Ergebnismenge: S = {Spitze; Kopf}. Oder anders ausgedrückt: S = {S; K}.
Wenn man sie zweimal wirft, dann können wir dies in einem Baumdiagramm darstellen:
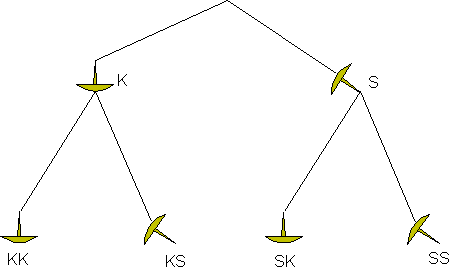
Die Ergebnismenge lässt sich anschließend aus dem Baumdiagramm ablesen: S = {(KK); (KS); (SK); (SS)}.
Es gibt also 4 mögliche Ergebnisse. Im Baumdiagramm führt jeder Pfad zu einem Ergebnis.
Übung 3:
In einer Urne liegen 2 grüne (g) und eine blaue (b) Kugel.
Dann zieht man zwei Kugeln. Dabei gilt folgende Vorschrift:
Nacheinander wird jeweils eine Kugel ohne Zurücklegen gezogen.
Stelle das Baumdiagramm auf und bilde danach die Ergebnismenge!
Die Lösung hierzu ist unten.
Übung 4:
In einer Urne liegen 2 grüne (g) und eine blaue (b) Kugel.
Dann zieht man zwei Kugeln. Dabei gilt folgende Vorschrift:
Nacheinander wird jeweils eine Kugel mit Zurücklegen gezogen.
Stelle das Baumdiagramm auf und bilde danach die Ergebnismenge!
Die Lösung hierzu ist unten.
Lösungen der Übungen:
- Die Wette über den Ausgang eines Fußballspiels kann man beliebig oft wiederholen.
Außerdem gibt es 3 mögliche Ergebnisse (Sieg, unentschieden, Niederlage).
Das Ergebnis ist schließlich nicht vorhersagbar.
Also ist die Wette über den Ausgang eines Fußballspiels ein Zufallsexperiment. - Hierzu drei Beispiele:
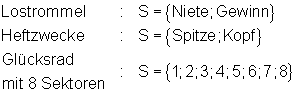
- Baumdiagramm hierzu:
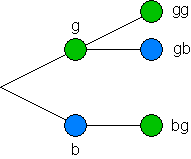
Ergebnismenge hierzu:
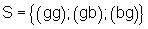
- Baumdiagramm hierzu:
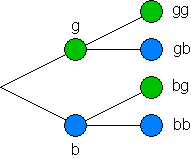
Ergebnismenge hierzu:
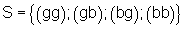
Hier findest du Aufgaben hierzu.
Und hier die Lösungen der Aufgaben.
Nächstes Thema: Ereignisse in der Wahrscheinlichkeitsrechnung.
Außerdem findest du hier eine Übersicht über alle Beiträge zum Thema Wahrscheinlichkeitsrechnung, darin auch Links zu Aufgaben.


